Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Baldwin, John
Kueker, David
and
VanDieren, Monica
2006.
Upward Stability Transfer for Tame Abstract Elementary Classes.
Notre Dame Journal of Formal Logic,
Vol. 47,
Issue. 2,
GROSSBERG, RAMI
and
VANDIEREN, MONICA
2006.
GALOIS-STABILITY FOR TAME ABSTRACT ELEMENTARY CLASSES.
Journal of Mathematical Logic,
Vol. 06,
Issue. 01,
p.
25.
GROSSBERG, RAMI
and
VANDIEREN, MONICA
2006.
CATEGORICITY FROM ONE SUCCESSOR CARDINAL IN TAME ABSTRACT ELEMENTARY CLASSES.
Journal of Mathematical Logic,
Vol. 06,
Issue. 02,
p.
181.
Kueker, David W.
2008.
Abstract elementary classes and infinitary logics.
Annals of Pure and Applied Logic,
Vol. 156,
Issue. 2-3,
p.
274.
Baldwin, John T.
and
Kolesnikov, Alexei
2009.
Categoricity, amalgamation, and tameness.
Israel Journal of Mathematics,
Vol. 170,
Issue. 1,
p.
411.
2011.
Issue Information.
Mathematical Logic Quarterly,
Vol. 57,
Issue. 2,
Lieberman, Michael
2011.
A topology for galois types in abstract elementary classes.
Mathematical Logic Quarterly,
Vol. 57,
Issue. 2,
p.
204.
Lieberman, Michael J.
2011.
Category-theoretic aspects of abstract elementary classes.
Annals of Pure and Applied Logic,
Vol. 162,
Issue. 11,
p.
903.
Lieberman, Michael J.
2013.
Rank Functions and Partial Stability Spectra for Tame Abstract Elementary Classes.
Notre Dame Journal of Formal Logic,
Vol. 54,
Issue. 2,
VanDieren, Monica M.
2013.
Erratum to “Categoricity in abstract elementary classes with no maximal models” [Ann. Pure Appl. Logic 141 (2006) 108–147].
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 2,
p.
131.
Jarden, Adi
and
Shelah, Saharon
2013.
Non-forking frames in abstract elementary classes.
Annals of Pure and Applied Logic,
Vol. 164,
Issue. 3,
p.
135.
Boney, Will
2014.
Tameness and extending frames.
Journal of Mathematical Logic,
Vol. 14,
Issue. 02,
p.
1450007.
Vasey, Sebastien
2016.
Building independence relations in abstract elementary classes.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 11,
p.
1029.
VanDieren, Monica M.
2016.
Superstability and symmetry.
Annals of Pure and Applied Logic,
Vol. 167,
Issue. 12,
p.
1171.
Vasey, Sebastien
2016.
Infinitary stability theory.
Archive for Mathematical Logic,
Vol. 55,
Issue. 3-4,
p.
567.
Baldwin, John T.
Koerwien, Martin
and
Souldatos, Ioannis
2016.
The joint embedding property and maximal models.
Archive for Mathematical Logic,
Vol. 55,
Issue. 3-4,
p.
545.
Boney, Will
Grossberg, Rami
Lieberman, Michael
Rosický, Jiří
and
Vasey, Sebastien
2016.
μ-Abstract elementary classes and other generalizations.
Journal of Pure and Applied Algebra,
Vol. 220,
Issue. 9,
p.
3048.
Vasey, Sebastien
2017.
Downward categoricity from a successor inside a good frame.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 3,
p.
651.
Boney, Will
Grossberg, Rami
VanDieren, Monica M.
and
Vasey, Sebastien
2017.
Superstability from categoricity in abstract elementary classes.
Annals of Pure and Applied Logic,
Vol. 168,
Issue. 7,
p.
1383.
VanDieren, Monica M.
and
Vasey, Sebastien
2017.
Symmetry in abstract elementary classes with amalgamation.
Archive for Mathematical Logic,
Vol. 56,
Issue. 3-4,
p.
423.
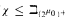 and K is categorical in some
and K is categorical in some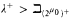 then K is categorical in μ for all μ
then K is categorical in μ for all μ 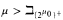 .
.