Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-25T19:58:55.847Z Has data issue: false hasContentIssue false
  • English
  • Français

Sheaves and Boolean valued model theory1

Published online by Cambridge University Press:  12 March 2014

George Loullis
George Loullis*
Affiliation:
Union College, Schenectady, New York 12308
Get access Rights & Permissions [Opens in a new window]

Extract

In recent years model theorists have been studying various sheaf-theoretic notions as they apply to model theory. For quite a while however, a sheaf of structures was considered to be just a local homeomorphism 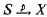between topological spaces such that each stalk Sx = p−1(x) is a model-theoretic structure and such that certain maps are continuous. Some of the model-theoretic work done with this notion of a sheaf of structures are the papers by Carson [2] and Macintyre [7]. Soon came the idea of considering a sheaf of structures not just as a collection of structures glued together in some continuous way, but rather as some sort of generalized structure. A significant model-theoretic study of sheaves in this new sense became possible only after the development of the theory of topoi. As F.W. Lawvere pointed out in [6], this represents the advance of mathematics (in our case the advance of model theory) from metaphysics to dialectics.

A topos is the rather ingenious evolution of the notion of a Grothendieck topos [13]. It provides us with the idea that an object of a topos (e.g. the topos of sheaves over a topological space) may be thought of as a generalized set. Furthermore, all first-order logical operations have an interpretation in a topos, hence we may talk about generalized structures. Angus Macintyre suggested that some of his model-theoretic results about sheaves of structures may be understood better and perhaps simplified by doing model theory inside a topos of sheaves.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 2 , June 1979 , pp. 153 - 183
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This is a revised version of part of the author's Ph.D. dissertation written at Yale University. The author wishes to express his gratitude to his advisor Professor Angus Macintyre for his guidance and encouragement.

References

BIBLIOGRAPHY

[1]Barr, M., Toposes without points, Journal of Pure and Applied Algebra, vol. 5 (1974), pp. 265–280.CrossRefGoogle Scholar
[2]Carson, A. B., The model-completion of the theory of commutative regular rings, Journal of Algebra, vol. 27 (1973), pp. 136–346.CrossRefGoogle Scholar
[3]Fulton, W., Algebraic curves, Benjamin, New York, 1969.Google Scholar
[4]Herrlich, H. and Strecker, G. E., Category theory, Allyn and Bacon, Boston, 1973.Google Scholar
[5]Higgs, D., A category approach to boolean-valued set theory, preprint, University of Waterloo.Google Scholar
[6]Lawvere, F. W., Continuously variable sets; Algebraic geometry = geometric logic, Proceedings of the Logic Colloquium, Bristol 1973, (Rose, H. E. and Shepherdson, J. C., Editors), North-Holland, Amsterdam, 1975.Google Scholar
[7]Macintyre, A., Model-completeness for sheaves of structures, Fundamenta Mathematical, vol. 81 (1973), pp. 73–89.CrossRefGoogle Scholar
[8]Mulvey, C., Intuitionistic algebra and representations of rings, Memoirs of the American Mathematical Society, No. 148, American Mathematical Society, Providence, RI, 1974.Google Scholar
[9]Pierce, R. S., Modules over commutative regular rings, Memoirs of the American Mathematical Society, No. 70, American Mathematical Society, Providence, RI, 1967.Google Scholar
[10]Robinson, A., Complete theories, North-Holland, Amsterdam, 1956.Google Scholar
[11]Robinson, A., Introduction to model-theory and to the metamathematics of algebra, North-Holland, Amsterdam, 1963.Google Scholar
[12]Saracino, D. and Weispfenning, V., On algebraic curves over commutative regular rings, Model theory and algebra: A memorial tribute to Abraham Robinson (Saracino, D. and Weispfenning, V., Editors), Lecture Notes in Mathematics, vol. 498 (1975), Springer-Verlag, Berlin and New York, pp. 307–383.CrossRefGoogle Scholar
[13] SGA 4, Théorie des topos et cohomologie étale des schémas, Lecture Notes in Mathematics, vol. 269 (1972), Springer-Verlag, Berlin and New York.Google Scholar
[14]Shorb, A. M., Contributions to Boolean-valued model theory, Ph.D. Thesis, University of Minnesota, 1969.Google Scholar
[15]Volger, H., Ultrafilters, ultrapowers and finiteness in a topos, Journal of Pure and Applied Algebra, vol. 6, (1975), pp. 345–356.CrossRefGoogle Scholar
[16]Wraith, G. C., Lectures on elementary topoi, Model theory and topoi (Lawvere, F. W., Maurer, C. and Wraith, G. C., Editors), Lecture Notes in Mathematics, vol. 445 (1975), Springer Verlag, Berlin and New York, pp. 114–206.CrossRefGoogle Scholar