Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Judah, H.
and
Shelah, S.
1994.
Killing Luzin and Sierpiński sets.
Proceedings of the American Mathematical Society,
Vol. 120,
Issue. 3,
p.
917.
Brendle, Jörg
1996.
Generic constructions of small sets of reals.
Topology and its Applications,
Vol. 71,
Issue. 2,
p.
125.
Shelah, Saharon
Brendle, Jörg
and
Shelah, Saharon
1999.
Ultrafilters on 𝜔-their ideals and their cardinal characteristics.
Transactions of the American Mathematical Society,
Vol. 351,
Issue. 7,
p.
2643.
Halbeisen, Lorenz
and
Löwe, Benedikt
2001.
Techniques for approaching the dual Ramsey property in the projective hierarchy.
Pacific Journal of Mathematics,
Vol. 200,
Issue. 1,
p.
119.
Кановей, Владимир Григорьевич
Kanovei, Vladimir Grigor'evich
Любецкий, Василий Александрович
and
Lyubetskii, Vasilii Aleksandrovich
2003.
О некоторых классических проблемах дескриптивной теории множеств.
Успехи математических наук,
Vol. 58,
Issue. 5,
p.
3.
Fischer, Vera
Friedman, Sy David
and
Khomskii, Yurii
2014.
Cichoń’s diagram, regularity properties and $${\varvec{\Delta}^1_3}$$ Δ 3 1 sets of reals.
Archive for Mathematical Logic,
Vol. 53,
Issue. 5-6,
p.
695.


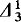 -sets of reals
-sets of reals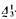 -sets of reals are measurable and (or) have the property of Baire and (or) are Ramsey. We will show that there is no implication between any of these properties for
-sets of reals are measurable and (or) have the property of Baire and (or) are Ramsey. We will show that there is no implication between any of these properties for 