No CrossRef data available.
Published online by Cambridge University Press: 12 March 2014
Nonstandard analysis was developed in [1] within a logic which has a language with finite types. In [2] and [3] the logic is first order and the language is that of set theory. The set theoretical approach can be described in the following setting.
Let 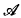 be a relational structure (A, ∈) where A is a nonempty set and ∈ is a restriction of the elementhood relation of set theory.
be a relational structure (A, ∈) where A is a nonempty set and ∈ is a restriction of the elementhood relation of set theory.
Let Ext be the wf (∀x)[(∃w)[w ∈ x] → [(∀y)(∀z) [z ∈ x ↔ z ∈ y] → x = y]]. Call 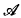 a fragment of set theory if
a fragment of set theory if 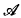 ⊧ Ext. By forming a nontrivial ultrapower of
⊧ Ext. By forming a nontrivial ultrapower of 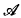 one obtains a structure
one obtains a structure 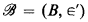 which, after canonically embedding
which, after canonically embedding 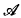 in
in 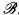 , becomes a proper elementary extension of
, becomes a proper elementary extension of 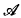 .
.
Let j embed 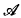 canonically in
canonically in 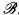 . Let
. Let 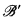 be the substructure (B′, ∈′) of
be the substructure (B′, ∈′) of 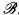 where B′ is the ∈′-closure of j(A) in B. That is, B′ is the smallest subset of B containing j(A) such that if b ∈ B, b′ ∈ B′ and
where B′ is the ∈′-closure of j(A) in B. That is, B′ is the smallest subset of B containing j(A) such that if b ∈ B, b′ ∈ B′ and 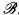 ⊧ b ∈ b′ then b ∈ B′.
⊧ b ∈ b′ then b ∈ B′.