Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-22T17:57:11.785Z Has data issue: false hasContentIssue false
  • English
  • Français

SET FORCING AND STRONG CONDENSATION FOR H(ω2)

Published online by Cambridge University Press:  13 March 2015

LIUZHEN WU
LIUZHEN WU*
Affiliation:
KURT GÖDEL RESEARCH CENTER FOR MATHEMATICAL LOGIC, UNIVERSITY OF VIENNA, WÄHRINGER STRASSE 25, A-1090 VIENNA, AUSTRIAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Axiom of Strong Condensation, first introduced by Woodin in [14], is an abstract version of the Condensation Lemma of L. In this paper, we construct a set-sized forcing to obtain Strong Condensation for H(ω2). As an application, we show that “ZFC + Axiom of Strong Condensation + 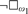”is consistent, which answers a question in [14]. As another application, we give a partial answer to a question of Jech by proving that “ZFC + there is a supercompact cardinal + any ideal on ω1 which is definable over H(ω2) is not precipitous” is consistent under sufficient large cardinal assumptions.

Keywords

03E3503E55Strong Condensationset forcingprecipitous idealsquare sequence
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 1 , March 2015 , pp. 56 - 84
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baumgartner, J. E. and Taylor, A. D., Saturation properties of ideals in generic extensions, II. Transactions of the American Mathematical Society, vol. 271 (1982), no. 2, pp. 587–609.Google Scholar
Beller, A., Jensen, R., and Welch, P., Coding the Universe, London Mathematical Society Lecture Note Series, vol. 47, Cambridge University Press, Cambridge, 1982.Google Scholar
Cummings, J., Iterated forcing and elementary embeddings, Handbook of set theory, Vols. 1, 2, 3, pp. 775–883, Springer, Dordrecht, 2010.Google Scholar
Devlin, K. J., Constructibility, Perspectives in Mathematical Logic, Springer, Berlin, 1984.Google Scholar
Foreman, M., Magidor, M., and Shelah, S., Martin’s maximum, saturated ideals, and nonregular ultrafilters, I. Annals of Mathematics, vol. 127 (1988), no. 1, pp. 1–47.Google Scholar
Friedman, S. D. and Koepke, P., An elementary approach to the fine structure of L. Bulletin of Symbolic Logic, vol. 3 (1997), no. 4, pp. 453–468.CrossRefGoogle Scholar
Friedman, S.-D. and Holy, P., Condensation and large cardinals. Fundamenta Mathematicae, vol. 215 (2011), no. 2, pp. 133–166.CrossRefGoogle Scholar
Jech, T., Magidor, M., Mitchell, W., and Prikry, K., Precipitous ideals, this Journal, vol. 45 (1980), no. 1, pp. 1–8.Google Scholar
Jensen, R. B., The fine structure of the constructible hierarchy. Annals of Mathematics Logic, vol. 4 (1972), pp. 229–308; erratum, ibid. vol. 4(1972), p. 443.CrossRefGoogle Scholar
Law, David R., An abstract condensation property, Ph. D. Dissertation, California Institute of Technology, Pasadena, CA 1994.Google Scholar
Schimmerling, E. and Velickovic, B., Collapsing functions, Mathematical Logic Quarterly vol. 50 (2004), no. 1, pp. 3–8.Google Scholar
Solovay, R. M., The independence of DC from AD, Cabal Seminar 76–77 (Proc. Caltech-UCLA Logic Sem., 1976–77), Lecture Notes in Mathematics, vol. 689, Springer, Berlin, pp. 171–183.Google Scholar
Wu, L., Sharp for the model of strong condensation, in preparationGoogle Scholar
Woodin, W. H., The Axiom of Determinacy, Forcing Axioms, and the Nonstationary Ideal, de Gruyter Series in Logic and its Applications, vol. 1, de Gruyter, Berlin, 1999.Google Scholar