Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-23T05:22:16.830Z Has data issue: false hasContentIssue false
  • English
  • Français

A SEPARATION RESULT FOR COUNTABLE UNIONS OF BOREL RECTANGLES

Published online by Cambridge University Press:  22 February 2019

DOMINIQUE LECOMTE
DOMINIQUE LECOMTE*
Affiliation:
UNIVERSITÉ PARIS 6, INSTITUT DE MATHÉMATIQUES DE JUSSIEU-PARIS RIVE GAUCHE PROJET ANALYSE FONCTIONNELLE, COULOIR 16-26 4ÈME ÉTAGE, CASE 247, 4, PLACE JUSSIEU 75 252 PARIS CEDEX 05, FRANCE AND UNIVERSITÉ DE PICARDIE, I.U.T. DE L’OISE, SITE DE CREIL 13, ALLÉE DE LA FAÏENCERIE 60 107 CREIL, FRANCE E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We provide dichotomy results characterizing when two disjoint analytic binary relations can be separated by a countable union of 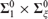${\bf{\Sigma }}_1^0 \times {\bf{\Sigma }}_\xi ^0$ sets, or by a 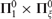${\bf{\Pi }}_1^0 \times {\bf{\Pi }}_\xi ^0$ set.

Keywords

Primary 03E15Secondary 54H05Borel classcountable Borel coloringBorel rectangle
Type
Articles
Information
The Journal of Symbolic Logic , Volume 84 , Issue 2 , June 2019 , pp. 517 - 532
Copyright
Copyright © The Association for Symbolic Logic 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Debs, G. and Raymond, J. S., Borel Liftings of Borel Sets: Some Decidable and Undecidable Statements, Memoirs of the American Mathematical Society, vol. 187, no. 876, American Mathematical Society, Providence, RI, 2007.Google Scholar
Harrington, L. A., Kechris, A. S., and Louveau, A., A Glimm-Effros dichotomy for Borel equivalence relations. Journal of the American Mathematical Society, vol. 3 (1990), pp. 903–928.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Springer-Verlag, New York, 1995.Google Scholar
Kechris, A. S., Solecki, S., and Todorčević, S., Borel chromatic numbers. Advances in Mathematics, vol. 141 (1999), pp. 1–44.Google Scholar
Kuratowski, C., Sur une généralisation de la notion d’homéomorphie. Fundamenta Mathematicae, vol. 22 (1934), no. 1, pp. 206–220.Google Scholar
Lecomte, D., On minimal nonpotentially closed subsets of the plane. Topology and its Applications, vol. 154 (2007), no. 1, pp. 241–262.Google Scholar
Lecomte, D., A dichotomy characterizing analytic graphs of uncountable Borel chromatic number in any dimension. Transactions of the American Mathematical Society, vol. 361 (2009), pp. 4181–4193.Google Scholar
Lecomte, D., How can we recognize potentially ${\bf{\Pi }}_\xi ^0$ subsets of the plane? Journal of Mathematical Logic, vol. 9 (2009), no. 1, pp. 39–62.Google Scholar
Lecomte, D., Potential Wadge Classes, Memoirs of the American Mathematical Society, vol. 221, no. 1038, American Mathematical Society, Providence, RI, 2013.Google Scholar
Lecomte, D. and Zelený, M., Baire-class ξ colorings: The first three levels. Transactions of the American Mathematical Society, vol. 366 (2014), no. 5, pp. 2345–2373.Google Scholar
Louveau, A., A separation theorem for $\Sigma _1^1$ sets. Transactions of the American Mathematical Society, vol. 260 (1980), pp. 363–378.Google Scholar
Louveau, A. and Raymond, J. S., Borel classes and closed games: Wadge-type and Hurewicz-type results. Transactions of the American Mathematical Society, vol. 304 (1987), pp. 431–467.Google Scholar
Miller, B. D., The graph-theoretic approach to descriptive set theory. Bulletin of Symbolic Logic, vol. 18 (2012), no. 4, pp. 554–575.Google Scholar
Moschovakis, Y. N., Descriptive Set Theory, North-Holland, Amsterdam, 1980.Google Scholar
Zamora, R., Separation of analytic sets by rectangles of low complexity. Topology and its Applications, vol. 182 (2015), pp. 77–97.Google Scholar