Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2025-01-03T11:30:00.106Z Has data issue: false hasContentIssue false
  • English
  • Français

Semantics of the infinitistic rules of proof

Published online by Cambridge University Press:  12 March 2014

Krzysztof Rafal Apt
Krzysztof Rafal Apt*
Affiliation:
Institute of Mathematics of the Polish Academy of Sciences, Warszawa, Poland
Get access Rights & Permissions [Opens in a new window]

Extract

This paper is devoted to the study of the infinitistic rules of proof i.e. those which admit an infinite number of premises. The best known of these rules is the ω-rule. Some properties of the ω-rule and its connection with the ω-models on the basis of the ω-completeness theorem gave impulse to the development of the theory of models for admissible fragments of the language 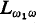. On the other hand the study of representability in second order arithmetic with the ω-rule added revealed for the first time an analogy between the notions of re-cursivity and hyperarithmeticity which had an important influence on the further development of generalized recursion theory.

The consideration of the subject of infinitistic rules in complete generality seems to be reasonable for several reasons. It is not completely clear which properties of the ω-rule were essential for the development of the above-mentioned topics. It is also worthwhile to examine the proof power of infinitistic rules of proof and what distinguishes them from finitistic rules of proof.

What seemed to us the appropriate point of view on this problem was the examination of the connection between the semantics and the syntax of the first order language equipped with an additional rule of proof.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 41 , Issue 1 , March 1976 , pp. 121 - 138
Copyright
Copyright © Association for Symbolic Logic 1976

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aczel, P. [1]: Representability in some systems of second order arithmetic, Israel Journal of Mathematica, vol. 8 (1970), pp. 309–328.CrossRefGoogle Scholar
Addison, J. W. [1]: Some consequences of the axiom of constructibility, Fundamenta Mathematicae, vol. 46 (1959), pp. 337–357.CrossRefGoogle Scholar
Apt, K. R. [1]: Infinitistic rules of proof and their semantics, Bulletin de l'Académie Polonaise des Sciences, vol. 21 (1973), pp. 879–886.Google Scholar
Apt, K. R. and Marek, W. [1]: Second order arithmetic and related topics, Annals of Mathematical Logic, vol. 6 (1974), pp. 177–229.CrossRefGoogle Scholar
Enderton, H. B. [1]: An infinitistic rule of proof, this Journal, vol. 32 (1967), pp. 447–452.Google Scholar
Enderton, H. B. and Friedman, H. [1]: Approximating the standard model for analysis, Fundamenta Mathematica, vol. 72 (1971), pp. 175–187.CrossRefGoogle Scholar
Feferman, S. [1]: Arithmetization of metamathematics in a general setting, Fundamenta Mathematicae, vol. 49 (1961), pp. 35–91.Google Scholar
Friedman, H. [1]: Countable models for set theories, Proceedings of the Cambridge Conference, Lecture Notes, Springer-Verlag, Berlin, 1973, pp. 539–573.Google Scholar
Mostowski, A. [1]: A formal system based on an infinitistic rule of proof, Infinitistic methods, PWN-Pergamon Press, Warszawa, 1961, pp. 141–166.Google Scholar
Orey, S. [1]: ω-consistency and related problems, this Journal, vol. 21 (1956), pp. 246–252.Google Scholar
Rogers, H. [1]: Theory of recursive functions and effective computability, McGraw-Hill, 1967 Google Scholar
Shoenfield, J. R. [1]: Mathematical logic, Addison-Wesley, 1967.Google Scholar
Shoenfield, J. R. [2]: The problem of predicativity, Essays in foundations of mathematics, Magnes Press, 1961, pp. 132–139.Google Scholar