Hostname: page-component-7bb8b95d7b-pwrkn Total loading time: 0 Render date: 2024-09-12T22:41:26.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Saturation of homogeneous resplendent models

Published online by Cambridge University Press:  12 March 2014

Julia F. Knight
Julia F. Knight*
Affiliation:
Department of Mathematics, University of Notre Dame, Notre Dame, Indiana 46556
Get access Rights & Permissions [Opens in a new window]

Extract

The complete diagram of a structure 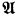, denoted by Dc(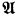), is the set of all sentences true in the structure (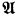, a)a∈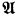. A structure 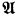is said to be resplendent if for every sentence θ involving a new relation symbol R in addition to symbols occurring in Dc(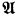), if θ is consistent with Dc(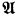), then there is a relation P on 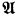such that 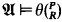(see[1]).

Baldwin asked whether a homogeneous recursively saturated structure is necessarily resplendent. Here it is shown that this need not be the case. It is shown that if 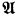is an uncountable homogeneous resplendent model of an unstable theory, then 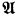must be saturated. The proof is related to the proof in [5] that an uncountable homogeneous recursively saturated model of first order Peano arithmetic must be saturated. The example for Baldwin's question is an uncountable homogeneous model 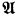for a particular unstable theory, such that 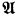is recursively saturated and omits some type. (The continuum hypothesis is needed to show the existence of such a model in power ℵ1.)

The proof of the main result requires two lemmas.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 1 , March 1986 , pp. 222 - 224
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barwise, J. and Schlipf, J., An introduction to recursively saturated and resplendent models, this Journal, vol. 41 (1976), pp. 531–536.Google Scholar
[2]Buechler, S., Expansions of models of ω-stable theories, this Journal, vol. 49 (1984), pp. 470–477.Google Scholar
[3]Buechler, S., Resplendency and recursive definability in ω-stable theories, Israel Journal of Mathematics, vol. 49 (1984), pp. 26–33.Google Scholar
[4]Kleene, S., Finite axiomatizability of theories in predicate calculus using additional predicate symbols, Memoirs of the American Mathematical Society, no. 10 (1952), pp. 27–68.Google Scholar
[5]Knight, J. and Nadel, M., Models of arithmetic and closed ideals, this Journal, vol. 47 (1982), pp. 833–840.Google Scholar
[6]Schmerl, J., Large resplendent models, handwritten notes.Google Scholar