Hostname: page-component-6bf8c574d5-8gtf8 Total loading time: 0 Render date: 2025-02-19T21:59:43.408Z Has data issue: false hasContentIssue false
  • English
  • Français

REVERSE MATHEMATICS, YOUNG DIAGRAMS, AND THE ASCENDING CHAIN CONDITION

Published online by Cambridge University Press:  19 June 2017

KOSTAS HATZIKIRIAKOU  and
STEPHEN G. SIMPSON
KOSTAS HATZIKIRIAKOU
Affiliation:
DEPARTMENT OF PRIMARY EDUCATION UNIVERSITY OF THESSALY ARGONAFTON & FILELLINON VOLOS38221, GREECE E-mail: [email protected]
STEPHEN G. SIMPSON
Affiliation:
DEPARTMENT OF MATHEMATICS 1326 STEVENSON CENTER VANDERBILT UNIVERSITY NASHVILLE, TN37240, USAURL: http://www.math.psu.edu/simpsonE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let S be the group of finitely supported permutations of a countably infinite set. Let 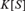$K[S]$ be the group algebra of S over a field K of characteristic 0. According to a theorem of Formanek and Lawrence, 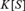$K[S]$ satisfies the ascending chain condition for two-sided ideals. We study the reverse mathematics of this theorem, proving its equivalence over 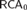$RC{A_0}$ (or even over 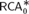$RCA_0^{\rm{*}}$) to the statement that 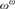${\omega ^\omega }$ is well ordered. Our equivalence proof proceeds via the statement that the Young diagrams form a well partial ordering.

Keywords

Primary 03B30Secondary 16P4016S3405A1703F15reverse mathematicsascending chain conditiongroup ringsYoung diagramspartition theorywell partial orderings
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 2 , June 2017 , pp. 576 - 589
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Andrews, G. E., The Theory of Partitions, Cambridge University Press, New York, 2014.Google Scholar
Aschenbrenner, M. and Yan Pong, W., Orderings of monomial ideals . Fundamenta Mathematicae, vol. 181 (2004), no. 1, pp. 27–74.Google Scholar
Chong, C.-T., Feng, Q., Slaman, T. A., and Woodin, W. H., editors, Infinity and Truth , Number 25 in IMS Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, World Scientific Publishing Co. Pte. Ltd., Singapore, 2014.Google Scholar
Curtis, C. W. and Reiner, I., Representation Theory of Finite Groups and Associative Algebras, Interscience, Wiley, Hoboken, NJ, 1962.Google Scholar
de Jongh, D. H. J. and Parikh, R., Well-partial orderings and hierarchies . Indagationes Mathematicae, vol. 80 (1977), no. 3, pp. 195–207.Google Scholar
Formanek, E. and Lawrence, J., The group algebra of the infinite symmetric group . Israel Journal of Mathematics, vol. 23 (1976), nos. 3 and 4, pp. 325–331.Google Scholar
Fulton, W., Young Tableaux With Applications to Representation Theory and Geometry, Number 35 in London Mathematical Society Student Texts, Cambridge University Press, New York, 1997.Google Scholar
Hatzikiriakou, K., Algebraic disguises of ${\rm{\Sigma }}_1^0$ induction . Archive for Mathematical Logic, vol. 29 (1989), no. 1, pp. 47–51.Google Scholar
Hatzikiriakou, K., Commutative algebra in subsystems of second order arithmetic, Ph.D. thesis, Pennsylvania State University, 1989.Google Scholar
Hatzikiriakou, K., A note on ordinal numbers and rings of formal power series . Archive for Mathematical Logic, vol. 33 (1994), no. 4, pp. 261–263.Google Scholar
Hilbert, D., Ueber die Theorie der algebraischen Formen . Mathematische Annalen, vol. 36 (1990), no. 4, pp. 473–534.Google Scholar
Hilbert, D., Über das Unendliche . Mathematische Annalen, vol. 95 (1926), no. 1, pp. 161–190.Google Scholar
Kerber, A., Representations of Permutation Groups I, Number 240 in Lecture Notes in Mathematics. Springer-Verlag, Berlin, 1971.Google Scholar
Kołodziejczyk, L. A. and Yokoyama, K., Categorical characterizations of the natural numbers require primitive recursion . Annals of Pure and Applied Logic, vol. 166 (2015), no. 2, pp. 219–231.Google Scholar
Maclagan, D., Antichains of monomial ideals are finite . Proceedings of the American Mathematical Society, vol. 129 (2000), no. 6, pp. 1609–1615.Google Scholar
Mansfield, R. and Weitkamp, G., Recursive Aspects of Descriptive Set Theory, Oxford Logic Guides, Oxford University Press, Oxford, 1985.Google Scholar
Marcone, A., WQO and BQO theory in subsystems of second order arithmetic. In [27], pp. 303–330, 2005.Google Scholar
Nash-Williams, C. St. J. A.. On better-quasi-ordering transfinite sequences . Mathematical Proceedings of the Cambridge Philosophical Society, vol. 64 (1968), no. 2, pp. 273–290.Google Scholar
Noether, M., Gordan, Paul. Mathematische Annalen, vol. 75 (1914), no. 1, pp. 1–41.Google Scholar
Robson, J. C., Well quasi-ordered sets and ideals in free semigroups and algebras . Journal of Algebra, vol. 55 (1978), no. 2, pp. 521–535.Google Scholar
Schmidt, D., Well-Partial Orderings and Their Maximal Order Types, Habilitationsschrift, Heidelberg University, Heidelberg, 1979.Google Scholar
Simpson, S. G., BQO theory and Fraïssé’s conjecture. In [16], pp. 124–138, 1985.Google Scholar
Simpson, S. G., Nichtbeweisbarkeit von gewissen kombinatorischen Eigenschaften endlicher Bäume . Archiv für mathematische Logik und Grundlagenforschung, vol. 25 (1985), no. 1, pp. 45–65.Google Scholar
Simpson, S. G., editor, Logic and Combinatorics, Contemporary Mathematics, American Mathematical Society, Providence, RI, 1987.Google Scholar
Simpson, S. G., Ordinal numbers and the Hilbert basis theorem, this Journal, vol. 53 (1988), no. 3, pp. 961–974.Google Scholar
Simpson, S. G., Partial realizations of Hilbert’s program, this Journal, vol. 53 (1988), no. 2, pp. 349–363.Google Scholar
Simpson, S. G., editor, Reverse Mathematics 2001, Number 21 in Lecture Notes in Logic, Association for Symbolic Logic, 2005.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1999. Second Edition, Perspectives in Logic, Association for Symbolic Logic, Cambridge University Press, New York, 2009.Google Scholar
Simpson, S. G., Baire categoricity and ${\rm{\Sigma }}_1^0$ induction . Notre Dame Journal of Formal Logic, vol. 55 (2014), no. 1, pp. 75–78.Google Scholar
Simpson, S. G., An objective justification for actual infinity? In [3], pp. 225–228, 2014.Google Scholar
Simpson, S. G., Toward objectivity in mathematics. In [3], pp. 157–169, 2014.Google Scholar
Simpson, S. G., Comparing WO $\left( {{\omega ^\omega }} \right)$ with ${\rm{\Sigma }}_2^0$ induction. arXiv:1508.02655, 11 August 2015. 6 pp.Google Scholar
Simpson, S. G. and Smith, R. L., Factorization of polynomials and ${\rm{\Sigma }}_1^0$ induction . Annals of Pure and Applied Logic, vol. 31 (1986), pp. 289–306.Google Scholar
Simpson, S. G. and Yokoyama, K., Reverse mathematics and Peano categoricity . Annals of Pure and Applied Logic, vol. 164 (2013), no. 3, pp. 284–293.Google Scholar
Tait, W. W., Finitism . Journal of Philosophy, vol. 78 (1981), no. 9, pp. 524–546.Google Scholar
van Engelen, F, Miller, A. W., and Steel, J., Rigid Borel sets and better quasi-order theory . In [24], pp. 199–222, 1987.Google Scholar
Yokoyama, K., On the strength of Ramsey’s Theorem without ${{\rm{\Sigma }}_1}$ -induction . Mathematical Logic Quarterly, vol. 59 (2013), nos. 1 and 2, pp. 108–111.Google Scholar