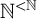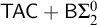1 Introduction
In this paper we study the computability-theoretic strength of the statement
![]() ${\mathsf {CAC\ for\ trees}}$
, which is a variation on the well-studied chain–antichain theorem (
${\mathsf {CAC\ for\ trees}}$
, which is a variation on the well-studied chain–antichain theorem (
![]() $\mathsf {CAC}$
). It turns out
$\mathsf {CAC}$
). It turns out
![]() ${\mathsf {CAC\ for\ trees}}$
has different characterizations, making it a robust notion, suitable for future studies in reverse mathematics.
${\mathsf {CAC\ for\ trees}}$
has different characterizations, making it a robust notion, suitable for future studies in reverse mathematics.
We are going to use two frameworks: reverse mathematics and computable reduction. For a good and more complete introduction to reverse mathematics, see Simpson [Reference Simpson18], or Hirschfeldt [Reference Hirschfeldt12] which also covers the computable reduction and classical results on Ramsey’s theorem.
Reverse mathematics is a foundational program which seeks to determine the optimal axioms to prove “ordinary” theorems. It itself uses the framework of subsystems of second-order arithmetic, with a base theory called
![]() $\mathsf {RCA}_0$
, which informally captures “computable mathematics.”
$\mathsf {RCA}_0$
, which informally captures “computable mathematics.”
Computable reduction makes precise the idea of being able to computably solve a problem P using another problem Q. A problem is defined as a
![]() $\Pi _2^1$
formula in the language of second-order arithmetic, thought to be of the form
$\Pi _2^1$
formula in the language of second-order arithmetic, thought to be of the form
![]() $\forall X (\psi (X)\implies \exists Y \varphi (X, Y))$
, where
$\forall X (\psi (X)\implies \exists Y \varphi (X, Y))$
, where
![]() $\psi $
and
$\psi $
and
![]() $\varphi $
are arithmetical formulas. An instance of a problem is a set X verifying
$\varphi $
are arithmetical formulas. An instance of a problem is a set X verifying
![]() $\psi (X)$
, and a solution of an instance X is a set Y such that
$\psi (X)$
, and a solution of an instance X is a set Y such that
![]() $\varphi (X, Y)$
. With this formalism, we say that “P is computably reducible to Q,” and we write
$\varphi (X, Y)$
. With this formalism, we say that “P is computably reducible to Q,” and we write
![]() $P\leqslant _c Q$
if for any instance I of P, there is an I-computable instance
$P\leqslant _c Q$
if for any instance I of P, there is an I-computable instance
![]() $\widehat {I}$
of Q, such that, for any solution
$\widehat {I}$
of Q, such that, for any solution
![]() $\widehat {S}$
of Q, there is an
$\widehat {S}$
of Q, there is an
![]() $\widehat {S}\oplus I$
-computable solution S of P.
$\widehat {S}\oplus I$
-computable solution S of P.
The early study of reverse mathematics has seen the emergence of four subsystems of second-order arithmetic, linearly ordered by the provability relation, such that most of the ordinary theorems are either provable in
![]() $\mathsf {RCA}_0$
, or equivalent in
$\mathsf {RCA}_0$
, or equivalent in
![]() $\mathsf {RCA}_0$
to one of them. These subsystems, together with
$\mathsf {RCA}_0$
to one of them. These subsystems, together with
![]() $\mathsf {RCA}_0$
, form the “Big Five.” Among the theorems studied in reverse mathematics, Ramsey’s theorem for pairs
$\mathsf {RCA}_0$
, form the “Big Five.” Among the theorems studied in reverse mathematics, Ramsey’s theorem for pairs
![]() $\mathsf {RT}_2^2$
plays an important role, since it is historically the first example of a natural statement which does not satisfy this empirical observation. The theorems we study in this paper are all consequences of
$\mathsf {RT}_2^2$
plays an important role, since it is historically the first example of a natural statement which does not satisfy this empirical observation. The theorems we study in this paper are all consequences of
![]() $\mathsf {RT}_2^2$
.
$\mathsf {RT}_2^2$
.
1.1 A chain–antichain theorem for trees
Among the consequences of Ramsey’s theorem for pairs, the chain–antichain theorem received a particular focus in reverse mathematics.
Definition 1.1 (
 $\mathsf {CAC}$
, chain–antichain theorem)
$\mathsf {CAC}$
, chain–antichain theorem)
Every infinite partial order has either an infinite chain or an infinite antichain.
![]() $\mathsf {CAC}$
was first studied in [Reference Hirschfeldt and Shore13] by Hirschfeldt and Shore, following a question raised by Cholak, Jockusch, and Slaman in [Reference Cholak, Jockusch and Slaman4, Question 13.8] asking whether or not
$\mathsf {CAC}$
was first studied in [Reference Hirschfeldt and Shore13] by Hirschfeldt and Shore, following a question raised by Cholak, Jockusch, and Slaman in [Reference Cholak, Jockusch and Slaman4, Question 13.8] asking whether or not
![]() $\mathsf {CAC}\implies \mathsf {RT}_2^2$
over
$\mathsf {CAC}\implies \mathsf {RT}_2^2$
over
![]() $\mathsf {RCA}_0$
, for which they proved the answer is negative (Corollary 3.12). The reciprocal
$\mathsf {RCA}_0$
, for which they proved the answer is negative (Corollary 3.12). The reciprocal
![]() $\mathsf {RCA}_0\vdash \mathsf {RT}_2^2\implies \mathsf {CAC}$
is easier to obtain, by defining a coloring such that
$\mathsf {RCA}_0\vdash \mathsf {RT}_2^2\implies \mathsf {CAC}$
is easier to obtain, by defining a coloring such that
![]() $\{x, y\}$
has color 1 if its elements are comparable, and 0 otherwise. Any homogeneous set for this coloring is either a chain or an antichain, depending on its color.
$\{x, y\}$
has color 1 if its elements are comparable, and 0 otherwise. Any homogeneous set for this coloring is either a chain or an antichain, depending on its color.
In this article, we focus on the special case where the order is the predecessor relation
![]() $\prec $
on a tree.
$\prec $
on a tree.
Definition 1.2 (
 ${\mathsf {CAC\ for\ trees}}$
)
${\mathsf {CAC\ for\ trees}}$
)
Every infinite subtree of
![]() $\mathbb {N}^{<\mathbb {N}}$
has an infinite path or an infinite antichain.
$\mathbb {N}^{<\mathbb {N}}$
has an infinite path or an infinite antichain.
This statement was first introduced by Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3], where the authors showed that every infinite computable tree must have either an infinite computable chain or an infinite
![]() $\Pi _1^0$
antichain. Furthermore, they showed that these bounds are optimal, by constructing an infinite computable tree which has no infinite
$\Pi _1^0$
antichain. Furthermore, they showed that these bounds are optimal, by constructing an infinite computable tree which has no infinite
![]() $\Sigma _1^0$
chain or antichain. They also showed that
$\Sigma _1^0$
chain or antichain. They also showed that
![]() (see Definition 2.1).
(see Definition 2.1).
1.2 Ramsey-like theorems
In [Reference Patey17], Patey identified a formal class of theorems, encompassing several statements surrounding Ramsey’s theorem. Indeed, many of them are of the form “for every coloring
![]() $f:[\mathbb {N}]^n\to k$
avoiding some set of forbidden patterns, there exists an infinite set
$f:[\mathbb {N}]^n\to k$
avoiding some set of forbidden patterns, there exists an infinite set
![]() $H\subseteq \mathbb {N}$
avoiding some other set of forbidden patterns (relative to f).”
$H\subseteq \mathbb {N}$
avoiding some other set of forbidden patterns (relative to f).”
For example the Erdős–Moser theorem (
![]() $\mathsf {EM}$
) asserts that, “for any coloring
$\mathsf {EM}$
) asserts that, “for any coloring
![]() $f:[\mathbb {N}]^2\to 2$
, there exists an infinite set
$f:[\mathbb {N}]^2\to 2$
, there exists an infinite set
![]() $H\subseteq \mathbb {N}$
which is transitive for f,” i.e.,
$H\subseteq \mathbb {N}$
which is transitive for f,” i.e.,
![]() $\forall i<2, \forall x{<} y{<} z\in H, f(x, y)=i\land f(y, z)=i\implies f(x, z)=i$
. In other terms, we want H to avoid the patterns that would make it not transitive for f, i.e.,
$\forall i<2, \forall x{<} y{<} z\in H, f(x, y)=i\land f(y, z)=i\implies f(x, z)=i$
. In other terms, we want H to avoid the patterns that would make it not transitive for f, i.e.,
![]() $f(x, y)=i\land f(y, z)=i\land f(x, z)=1-i$
for any
$f(x, y)=i\land f(y, z)=i\land f(x, z)=1-i$
for any
![]() $i<2$
. Another example comes from
$i<2$
. Another example comes from
![]() $\mathsf {ADS}$
which is equivalent over
$\mathsf {ADS}$
which is equivalent over
![]() $\mathsf {RCA}_0$
(see [Reference Hirschfeldt and Shore13, Theorem 5.3]) to the statement “for any transitive coloring
$\mathsf {RCA}_0$
(see [Reference Hirschfeldt and Shore13, Theorem 5.3]) to the statement “for any transitive coloring
![]() $f:[\mathbb {N}]^2\to 2$
(i.e., avoiding certain patterns), there exists an infinite set
$f:[\mathbb {N}]^2\to 2$
(i.e., avoiding certain patterns), there exists an infinite set
![]() $H\subseteq \mathbb {N}$
which is f-homogeneous.” With these definitions, one sees that
$H\subseteq \mathbb {N}$
which is f-homogeneous.” With these definitions, one sees that
![]() $\mathsf {RT}_2^2$
is equivalent to
$\mathsf {RT}_2^2$
is equivalent to
![]() $\mathsf {EM}+\mathsf {ADS}$
over
$\mathsf {EM}+\mathsf {ADS}$
over
![]() $\mathsf {RCA}_0$
, since
$\mathsf {RCA}_0$
, since
![]() $\mathsf {EM}$
takes any coloring and “turns it into” a transitive one, and
$\mathsf {EM}$
takes any coloring and “turns it into” a transitive one, and
![]() $\mathsf {ADS}$
takes any transitive coloring and finds an infinite set which is homogeneous for it.
$\mathsf {ADS}$
takes any transitive coloring and finds an infinite set which is homogeneous for it.
Forbidden patterns on three variables and two colors are generated by the following three basic patterns:
-
(1)
 $f(x, y)=i\land f(y, z)=i\land f(x, z)=1-i.$
$f(x, y)=i\land f(y, z)=i\land f(x, z)=1-i.$
-
(2)
 $f(x, y)=i\land f(y, z)=1-i\land f(x, z)=i.$
$f(x, y)=i\land f(y, z)=1-i\land f(x, z)=i.$
-
(3)
 $f(x, y)=1-i\land f(y, z)=i\land f(x, z)=i.$
$f(x, y)=1-i\land f(y, z)=i\land f(x, z)=i.$
Avoiding them respectively leads to transitivity, semi-ancestry, and semi-heredity (for the color i). Each of them generates two Ramsey-like statements, one restricting the input coloring, and one restricting the output infinite set, namely “for any 2-coloring of pairs avoiding the forbidden pattern, there exists an infinite homogeneous set” and “for any 2-coloring of pairs, there exists an infinite set
![]() $H\subseteq \mathbb {N}$
which avoids the forbidden pattern.” We now survey the known results about these three patterns.
$H\subseteq \mathbb {N}$
which avoids the forbidden pattern.” We now survey the known results about these three patterns.
1.2.1 Transitivity
The statement “for any 2-coloring of pairs, there exists an infinite set which is transitive for some color” is a weaker version of
![]() $\mathsf {EM}$
. The Erdös–Moser theorem was proven to be strictly weaker than Ramsey’s theorem for pairs over
$\mathsf {EM}$
. The Erdös–Moser theorem was proven to be strictly weaker than Ramsey’s theorem for pairs over
![]() $\mathsf {RCA}_0$
by Lerman, Solomon, and Towsner [Reference Lerman, Solomon and Towsner16, Corollary 1.16]. On the other hand, the statement “for any 2-coloring of pairs which is transitive for some color, there exists an infinite homogeneous set” is equivalent to
$\mathsf {RCA}_0$
by Lerman, Solomon, and Towsner [Reference Lerman, Solomon and Towsner16, Corollary 1.16]. On the other hand, the statement “for any 2-coloring of pairs which is transitive for some color, there exists an infinite homogeneous set” is equivalent to
![]() $\mathsf {CAC}$
(see [Reference Hirschfeldt and Shore13, Theorem 5.2]), which is also known to be strictly weaker than
$\mathsf {CAC}$
(see [Reference Hirschfeldt and Shore13, Theorem 5.2]), which is also known to be strictly weaker than
![]() $\mathsf {RT}_2^2$
over
$\mathsf {RT}_2^2$
over
![]() $\mathsf {RCA}_0$
(see [Reference Hirschfeldt and Shore13, Corollary 3.12]).
$\mathsf {RCA}_0$
(see [Reference Hirschfeldt and Shore13, Corollary 3.12]).
1.2.2 Semi-ancestry
The statement “for any 2-coloring of pairs which has semi-ancestry for some color, there exists an infinite homogeneous set” is a consequence of the statement
![]() $\mathsf {STRIV}$
, defined by Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8, Statement 5.12]), because a 2-coloring is semi-trivial if and only if it has semi-ancestry. And
$\mathsf {STRIV}$
, defined by Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8, Statement 5.12]), because a 2-coloring is semi-trivial if and only if it has semi-ancestry. And
![]() $\mathsf {STRIV}$
itself is equivalent to
$\mathsf {STRIV}$
itself is equivalent to
![]() $\forall k, \mathsf {RT}_k^1$
(see the remark below its definition). The statement “for any 2-coloring of pairs, there exists an infinite set which has semi-ancestry for some color” is equivalent to
$\forall k, \mathsf {RT}_k^1$
(see the remark below its definition). The statement “for any 2-coloring of pairs, there exists an infinite set which has semi-ancestry for some color” is equivalent to
![]() $\mathsf {RT}_2^2$
(see Proposition 6.11).
$\mathsf {RT}_2^2$
(see Proposition 6.11).
1.2.3 Semi-heredity
The statement “for any 2-coloring of pairs which is semi-hereditary for some color, there exists an infinite homogeneous set” is the statement
![]() $\mathsf {SHER}$
, which was first introduced by Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8, Statement 5.11]. In Section 6, we will show that it is equivalent to
$\mathsf {SHER}$
, which was first introduced by Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8, Statement 5.11]. In Section 6, we will show that it is equivalent to
![]() ${\mathsf {CAC\ for\ trees}}$
. Finally, the statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color” is equivalent to
${\mathsf {CAC\ for\ trees}}$
. Finally, the statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color” is equivalent to
![]() $\mathsf {RT}_2^2$
(see Corollary 6.13).
$\mathsf {RT}_2^2$
(see Corollary 6.13).
1.3 Notation
Let the symbols
![]() $\exists ^{\infty } x$
and
$\exists ^{\infty } x$
and
![]() $\forall ^{\infty } x$
be abbreviations for
$\forall ^{\infty } x$
be abbreviations for
![]() $\forall y, \exists x>y$
and
$\forall y, \exists x>y$
and
![]() $\exists y, \forall x>y$
, respectively. In particular they are the dual of each other.
$\exists y, \forall x>y$
, respectively. In particular they are the dual of each other.
Given
![]() $x, y\in \mathbb {N}\cup \{\pm \infty \}$
, we define
$x, y\in \mathbb {N}\cup \{\pm \infty \}$
, we define
![]() , an inequality being strict when its respective bracket is flipped, e.g.,
, an inequality being strict when its respective bracket is flipped, e.g.,
![]() . As in set theory, an integer n can also represent the set of all integers strictly smaller to it, i.e.,
. As in set theory, an integer n can also represent the set of all integers strictly smaller to it, i.e.,
![]() . Moreover
. Moreover
![]() $\langle -, \ldots , - \rangle $
represents a bijection from
$\langle -, \ldots , - \rangle $
represents a bijection from
![]() $\mathbb {N}^n$
to
$\mathbb {N}^n$
to
![]() $\mathbb {N}$
(for some n), which verifies
$\mathbb {N}$
(for some n), which verifies
![]() $\forall x, y\in \mathbb {N}, \langle x_1,\ldots , x_k\rangle \geqslant \max \{x_1,\ldots , x_k\}$
and which is increasing on each variable. Given a set
$\forall x, y\in \mathbb {N}, \langle x_1,\ldots , x_k\rangle \geqslant \max \{x_1,\ldots , x_k\}$
and which is increasing on each variable. Given a set
![]() $A\subseteq \mathbb {N}$
, we denote by
$A\subseteq \mathbb {N}$
, we denote by
![]() $\chi _A$
its indicator function.
$\chi _A$
its indicator function.
A string is a finite sequence of integers, and the set of all strings is denoted
![]() $\mathbb {N}^{<\mathbb {N}}$
. In particular, a binary string is a finite sequence of 0 and 1, and the set of all binary strings is denoted
$\mathbb {N}^{<\mathbb {N}}$
. In particular, a binary string is a finite sequence of 0 and 1, and the set of all binary strings is denoted
![]() $2^{<\mathbb {N}}$
. The length of a given string
$2^{<\mathbb {N}}$
. The length of a given string
![]() $\sigma :n\to \mathbb {N}$
is the integer
$\sigma :n\to \mathbb {N}$
is the integer
![]() $|\sigma |\mathrel {\mathop :}= n$
. The empty string
$|\sigma |\mathrel {\mathop :}= n$
. The empty string
![]() $\varnothing \to \mathbb {N}$
is denoted
$\varnothing \to \mathbb {N}$
is denoted
![]() $\varepsilon $
. Given two strings
$\varepsilon $
. Given two strings
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
of respective length
$\tau $
of respective length
![]() $\ell $
and m, we define their concatenation as the finite sequence
$\ell $
and m, we define their concatenation as the finite sequence
![]() $\sigma \cdot \tau :\ell +m\to \mathbb {N}$
which, given
$\sigma \cdot \tau :\ell +m\to \mathbb {N}$
which, given
![]() $j<\ell +m$
, associates
$j<\ell +m$
, associates
![]() $\sigma (j)$
if
$\sigma (j)$
if
![]() $j<\ell $
, and
$j<\ell $
, and
![]() $\tau (j-\ell )$
otherwise. So we usually write a string
$\tau (j-\ell )$
otherwise. So we usually write a string
![]() $\sigma :n\to \mathbb {N}$
as
$\sigma :n\to \mathbb {N}$
as
![]() $\sigma _0\cdot \ldots \cdot \sigma _{n-1}$
, where
$\sigma _0\cdot \ldots \cdot \sigma _{n-1}$
, where
![]() $\forall j<n, \sigma _j\mathrel {\mathop :}= \sigma (j)$
. We define the partial order on strings “is prefix of,” denoted
$\forall j<n, \sigma _j\mathrel {\mathop :}= \sigma (j)$
. We define the partial order on strings “is prefix of,” denoted
![]() $\prec $
, by
$\prec $
, by
![]() $\sigma \prec \tau \iff |\sigma |<|\tau |\land \forall j<|\sigma |, \sigma (j)=\tau (j)$
, and denote by
$\sigma \prec \tau \iff |\sigma |<|\tau |\land \forall j<|\sigma |, \sigma (j)=\tau (j)$
, and denote by
![]() $\preccurlyeq $
its reflexive closure. When two strings
$\preccurlyeq $
its reflexive closure. When two strings
![]() $\sigma $
and
$\sigma $
and
![]() $\tau $
are incomparable for
$\tau $
are incomparable for
![]() $\prec $
, we write
$\prec $
, we write
![]() $\sigma \bot \tau $
.
$\sigma \bot \tau $
.
A tree T is a subset of
![]() $\mathbb {N}^{<\mathbb {N}}$
which is downward closed for
$\mathbb {N}^{<\mathbb {N}}$
which is downward closed for
![]() $\prec $
, i.e.,
$\prec $
, i.e.,
![]() $\forall \sigma \in T, \tau \prec \sigma \implies \tau \in T$
. A binary tree is a subset of
$\forall \sigma \in T, \tau \prec \sigma \implies \tau \in T$
. A binary tree is a subset of
![]() $2^{<\mathbb {N}}$
which is downward closed for
$2^{<\mathbb {N}}$
which is downward closed for
![]() $\prec $
. A subset
$\prec $
. A subset
![]() $S\subseteq T$
of a tree is a chain when it is linearly ordered for
$S\subseteq T$
of a tree is a chain when it is linearly ordered for
![]() $\prec $
, and it is an antichain when its elements are pairwise incomparable for
$\prec $
, and it is an antichain when its elements are pairwise incomparable for
![]() $\prec $
.
$\prec $
.
1.4 Organization of the paper
In Section 2, we prove the robustness of
![]() ${\mathsf {CAC\ for\ trees}}$
in reverse mathematics and over the computable reduction, by proving its equivalence with several variants of the statement. In Section 3, we provide a probabilistic proof of
${\mathsf {CAC\ for\ trees}}$
in reverse mathematics and over the computable reduction, by proving its equivalence with several variants of the statement. In Section 3, we provide a probabilistic proof of
![]() ${\mathsf {CAC\ for\ trees}}$
, and give a precise analysis of this proof in terms of
${\mathsf {CAC\ for\ trees}}$
, and give a precise analysis of this proof in terms of
![]() $\mathsf {DNC}$
functions. In Section 4 we show that both
$\mathsf {DNC}$
functions. In Section 4 we show that both
![]() $\mathsf {ADS}$
and
$\mathsf {ADS}$
and
![]() $\mathsf {EM}$
imply
$\mathsf {EM}$
imply
![]() ${\mathsf {CAC\ for\ trees}}$
. In Section 5 we prove there is a computable instance of
${\mathsf {CAC\ for\ trees}}$
. In Section 5 we prove there is a computable instance of
![]() $\mathsf {TAC}$
whose solutions are all of hyperimmune degree, with almost explicit witness. In particular we show a computable instance of
$\mathsf {TAC}$
whose solutions are all of hyperimmune degree, with almost explicit witness. In particular we show a computable instance of
![]() $\mathsf {TAC}$
can avoid a uniform sequence of
$\mathsf {TAC}$
can avoid a uniform sequence of
![]() $\Delta _2^0$
sets. In Section 6, we show the equivalence between
$\Delta _2^0$
sets. In Section 6, we show the equivalence between
![]() ${\mathsf {CAC\ for\ trees}}$
and
${\mathsf {CAC\ for\ trees}}$
and
![]() $\mathsf {SHER}$
. In Section 7, we explore the relations between stable versions of previously mentioned statements, namely
$\mathsf {SHER}$
. In Section 7, we explore the relations between stable versions of previously mentioned statements, namely
![]() ${\mathsf {CAC\ for\ trees}}$
,
${\mathsf {CAC\ for\ trees}}$
,
![]() $\mathsf {ADS}$
, and
$\mathsf {ADS}$
, and
![]() $\mathsf {SHER}$
, leading to the result that
$\mathsf {SHER}$
, leading to the result that
![]() ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
admits low solutions. Finally, in Section 8, we conclude the paper with remaining open questions and summary diagrams.
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
admits low solutions. Finally, in Section 8, we conclude the paper with remaining open questions and summary diagrams.
2 Equivalent definitions
In this section, we study some variations of
![]() ${\mathsf {CAC\ for\ trees}}$
, and prove they are all equivalent. We also study
${\mathsf {CAC\ for\ trees}}$
, and prove they are all equivalent. We also study
![]() $\mathsf {TAC}$
and show that
$\mathsf {TAC}$
and show that
![]() $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
is equivalent to
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
is equivalent to
![]() ${\mathsf {CAC\ for\ trees}}$
. We start by defining these statements.
${\mathsf {CAC\ for\ trees}}$
. We start by defining these statements.
Definition 2.1 (CAC for c.e. (binary) trees)
Every infinite c.e. (binary) subtree of
![]() $\mathbb {N}^{<\mathbb {N}}$
has an infinite path or an infinite antichain.
$\mathbb {N}^{<\mathbb {N}}$
has an infinite path or an infinite antichain.
Remark 2.2. In the context of reverse mathematics “being c.e.” is a notion that is relative to the model considered, i.e., an object is c.e. when it can be approximated in a c.e. manner by objects from the model.
Definition 2.3 (Completely branching tree)
A node
![]() $\sigma $
of a tree
$\sigma $
of a tree
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
is a split node when there is
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
is a split node when there is
![]() $n_0, n_1\in \mathbb {N}$
such that
$n_0, n_1\in \mathbb {N}$
such that
![]() $\forall i<2, \sigma \cdot n_i\in T$
. In particular, if T is a binary tree, then
$\forall i<2, \sigma \cdot n_i\in T$
. In particular, if T is a binary tree, then
![]() $\sigma $
is a split node when both
$\sigma $
is a split node when both
![]() $\sigma \cdot 0\in T$
and
$\sigma \cdot 0\in T$
and
![]() $\sigma \cdot 1\in T$
. A tree
$\sigma \cdot 1\in T$
. A tree
![]() $T\subseteq 2^{<\mathbb {N}}$
is completely branching when, for any of its node
$T\subseteq 2^{<\mathbb {N}}$
is completely branching when, for any of its node
![]() $\sigma $
, if
$\sigma $
, if
![]() $\sigma $
is not a leaf then it is a split node.
$\sigma $
is not a leaf then it is a split node.
The following statement was introduced by Conidis [Reference Conidis6] (personal communication), motivated by the reverse mathematics of commutative Noetherian rings.
Definition 2.4 (
 $\mathsf {TAC}$
[Reference Conidis6], tree antichain theorem)
$\mathsf {TAC}$
[Reference Conidis6], tree antichain theorem)
Any infinite c.e. subtree of
![]() $2^{<\mathbb {N}}$
which is completely branching, contains an infinite antichain.
$2^{<\mathbb {N}}$
which is completely branching, contains an infinite antichain.
Conidis proved that
![]() $\mathsf {TAC}$
follows from
$\mathsf {TAC}$
follows from
![]() $\mathsf {CAC}$
over
$\mathsf {CAC}$
over
![]() $\mathsf {RCA}_0$
, and constructed an instance of
$\mathsf {RCA}_0$
, and constructed an instance of
![]() $\mathsf {TAC}$
, all of whose solutions are of hyperimmune degree. In particular,
$\mathsf {TAC}$
, all of whose solutions are of hyperimmune degree. In particular,
![]() $\mathsf {RCA}_0 + \mathsf {WKL} \nvdash \mathsf {TAC}$
. Now we can proceed with the proof of the equivalence.
$\mathsf {RCA}_0 + \mathsf {WKL} \nvdash \mathsf {TAC}$
. Now we can proceed with the proof of the equivalence.
Theorem 2.5. The following statements are equivalent over
![]() $\mathsf {RCA}_0$
and computable reduction:
$\mathsf {RCA}_0$
and computable reduction:
-
(1)
 ${\mathsf {CAC\ for\ trees}}$
.
${\mathsf {CAC\ for\ trees}}$
. -
(2)
 ${\mathsf {CAC\ for\ c.e.\ trees}}$
.
${\mathsf {CAC\ for\ c.e.\ trees}}$
. -
(3)
 ${\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
.
${\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
. -
(4)
 $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
.
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
.
Proof
![]() $(2) \implies (1)$
and
$(2) \implies (1)$
and
![]() $(2) \implies (3)$
are immediate.
$(2) \implies (3)$
are immediate.
![]() $(3) \implies (4)$
is Propositions 2.6 and 2.7.
$(3) \implies (4)$
is Propositions 2.6 and 2.7.
![]() $(4) \implies (2)$
is Proposition 2.8.
$(4) \implies (2)$
is Proposition 2.8.
![]() $(1) \implies (2)$
is Proposition 2.9.
$(1) \implies (2)$
is Proposition 2.9.
We shall see in Section 3 that the use of
![]() $\mathsf {B}\Sigma ^0_2$
is necessary in the equivalence above, as
$\mathsf {B}\Sigma ^0_2$
is necessary in the equivalence above, as
![]() $\mathsf {TAC}$
does not imply
$\mathsf {TAC}$
does not imply
![]() $\mathsf {B}\Sigma ^0_2$
over
$\mathsf {B}\Sigma ^0_2$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proposition 2.6.
![]() $\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ c.e.\ binary\ trees}}\implies \mathsf {TAC}$
and
$\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ c.e.\ binary\ trees}}\implies \mathsf {TAC}$
and
![]() $\mathsf {TAC}\leqslant _c{\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
.
$\mathsf {TAC}\leqslant _c{\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
.
Proof Let
![]() $T\subseteq 2^{<\mathbb {N}}$
be an infinite completely branching c.e. tree. By the statement
$T\subseteq 2^{<\mathbb {N}}$
be an infinite completely branching c.e. tree. By the statement
![]() ${\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
, either there is an infinite antichain, or an infinite path P. In the former case, we are done. In the latter case, using the fact that T is completely branching, the set
${\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
, either there is an infinite antichain, or an infinite path P. In the former case, we are done. In the latter case, using the fact that T is completely branching, the set
![]() $\{\sigma \cdot (1-i)\mid \sigma \cdot i\prec P\}$
is an infinite antichain of T.
$\{\sigma \cdot (1-i)\mid \sigma \cdot i\prec P\}$
is an infinite antichain of T.
Proposition 2.7.
![]() $\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ c.e.\ binary\ trees}}\implies \forall k, \mathsf {RT}^1_k$
and
$\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ c.e.\ binary\ trees}}\implies \forall k, \mathsf {RT}^1_k$
and
![]() $\kern1pt\forall k, \mathsf {RT}^1_k\leqslant _c{\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
.
$\kern1pt\forall k, \mathsf {RT}^1_k\leqslant _c{\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
.
Proof Let
![]() $f:\mathbb {N}\to k$
be a coloring, there are two possibilities. Either
$f:\mathbb {N}\to k$
be a coloring, there are two possibilities. Either
![]() $\exists i<k, \exists ^{\infty } x, f(x)=i$
, in which case there is an infinite computable f-homogeneous set. Otherwise
$\exists i<k, \exists ^{\infty } x, f(x)=i$
, in which case there is an infinite computable f-homogeneous set. Otherwise
![]() $\forall i<k, \forall ^{\infty } x, f(x)\neq i$
, in which case we define an infinite binary
$\forall i<k, \forall ^{\infty } x, f(x)\neq i$
, in which case we define an infinite binary
![]() $c.e.$
tree T, via a strictly increasing sequence of computable trees
$c.e.$
tree T, via a strictly increasing sequence of computable trees
![]() $(T_j)_{j\in \mathbb {N}}$
defined by
$(T_j)_{j\in \mathbb {N}}$
defined by
![]() $T_0 \mathrel {\mathop :}= \{0^i\mid i<k\}$
and
$T_0 \mathrel {\mathop :}= \{0^i\mid i<k\}$
and
![]() $T_{s+1} \mathrel {\mathop :}= T_s\cup \{0^{f(s)}\cdot 1^{m+1}\}$
, where m is the number of
$T_{s+1} \mathrel {\mathop :}= T_s\cup \{0^{f(s)}\cdot 1^{m+1}\}$
, where m is the number of
![]() $x<s$
such that
$x<s$
such that
![]() $f(x)=f(s)$
.
$f(x)=f(s)$
.
Every antichain in T is of size at most k, thus, by
![]() ${\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
, T must contain an infinite path, and so
${\mathsf {CAC\ for\ c.e.\ binary\ trees}}$
, T must contain an infinite path, and so
![]() $\exists i<k, \exists ^{\infty } x, f(x)=i$
, which is a contradiction.
$\exists i<k, \exists ^{\infty } x, f(x)=i$
, which is a contradiction.
Proposition 2.8.
![]() $\mathsf {RCA}_0\vdash \mathsf {TAC}+\mathsf {B}\Sigma ^0_2\implies {\mathsf {CAC\ for\ c.e.\ trees}}$
and
$\mathsf {RCA}_0\vdash \mathsf {TAC}+\mathsf {B}\Sigma ^0_2\implies {\mathsf {CAC\ for\ c.e.\ trees}}$
and
![]() ${\mathsf {CAC\ for\ c.e.\ trees}} \leqslant _c \mathsf {TAC}$
${\mathsf {CAC\ for\ c.e.\ trees}} \leqslant _c \mathsf {TAC}$
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite c.e. tree. We can deal with two cases directly: when T has a node with infinitely many immediate children, as they contain a computable infinite antichain; and when T has finitely many split nodes, in which case it has finitely many paths
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite c.e. tree. We can deal with two cases directly: when T has a node with infinitely many immediate children, as they contain a computable infinite antichain; and when T has finitely many split nodes, in which case it has finitely many paths
![]() $P_0, \ldots , P_{k-1}$
, which are all computable. Moreover one of them is infinite, as otherwise they would all be finite, i.e.,
$P_0, \ldots , P_{k-1}$
, which are all computable. Moreover one of them is infinite, as otherwise they would all be finite, i.e.,
![]() $\forall i<k, \exists s, \forall n>s, n\notin P_i$
, and thus their union would be finite since
$\forall i<k, \exists s, \forall n>s, n\notin P_i$
, and thus their union would be finite since
![]() $\mathsf {B}\Pi ^0_1$
(which is equivalent to
$\mathsf {B}\Pi ^0_1$
(which is equivalent to
![]() $\mathsf {B}\Sigma ^0_2$
) yields
$\mathsf {B}\Sigma ^0_2$
) yields
![]() $\exists b, \forall i<k, \exists s<b, \forall n>s, n\notin P_i$
. But since
$\exists b, \forall i<k, \exists s<b, \forall n>s, n\notin P_i$
. But since
![]() $T=\bigcup _{i<k} P_i$
, this would lead to a contradiction.
$T=\bigcup _{i<k} P_i$
, this would lead to a contradiction.
A split triple of T is a triple
![]() $(\mu , n_0, n_1)\in T\times \mathbb {N}\times \mathbb {N}$
such that
$(\mu , n_0, n_1)\in T\times \mathbb {N}\times \mathbb {N}$
such that
![]() $\mu , \mu \cdot n_0, \mu \cdot n_1 \in T$
. In particular,
$\mu , \mu \cdot n_0, \mu \cdot n_1 \in T$
. In particular,
![]() $\mu $
is a split node in T.
$\mu $
is a split node in T.
Idea. The general idea is to build greedily a completely branching c.e. tree S by looking for split triples in T, and mapping them to split nodes in S. This correspondence is witnessed by an injective function
![]() $f : S \to T$
that will be constructed alongside S. The main difficulty is that, since T is c.e., a split node
$f : S \to T$
that will be constructed alongside S. The main difficulty is that, since T is c.e., a split node
![]() $\rho $
can be discovered after
$\rho $
can be discovered after
![]() $\mu $
even though
$\mu $
even though
![]() $\rho \prec \mu $
, which means that we will not be able to ensure that S can be embedded in T. In particular, f will not be a tree morphism. However, the only property that needs to be ensured is that for every infinite antichain A of S, the set
$\rho \prec \mu $
, which means that we will not be able to ensure that S can be embedded in T. In particular, f will not be a tree morphism. However, the only property that needs to be ensured is that for every infinite antichain A of S, the set
![]() $f(A)$
will be an infinite antichain of T. To guarantee this, the function f needs to verify
$f(A)$
will be an infinite antichain of T. To guarantee this, the function f needs to verify
During the construction, we are going to associate with each node
![]() $\sigma \in S$
a set
$\sigma \in S$
a set
![]() $N_{\sigma } \subseteq T$
, which might decrease in size over time (
$N_{\sigma } \subseteq T$
, which might decrease in size over time (
![]() $N^0_{\sigma } \supseteq N^1_{\sigma } \supseteq \dots $
), with the property that at every step s, the elements of
$N^0_{\sigma } \supseteq N^1_{\sigma } \supseteq \dots $
), with the property that at every step s, the elements of
![]() $\{ N^s_{\sigma } : \sigma \in S\}$
are pairwise disjoint, and their union contains cofinitely many elements of T. The role of
$\{ N^s_{\sigma } : \sigma \in S\}$
are pairwise disjoint, and their union contains cofinitely many elements of T. The role of
![]() $N_{\sigma }$
is to indicate that “if a split triple is found in
$N_{\sigma }$
is to indicate that “if a split triple is found in
![]() $N_{\sigma }$
, then the nodes in S, associated via f, must be above
$N_{\sigma }$
, then the nodes in S, associated via f, must be above
![]() $\sigma $
.”
$\sigma $
.”
Construction. Initially,
![]() $N^0_{\varepsilon } \mathrel {\mathop :}= T$
,
$N^0_{\varepsilon } \mathrel {\mathop :}= T$
,
![]() $S \mathrel {\mathop :}= \{\varepsilon \}$
and
$S \mathrel {\mathop :}= \{\varepsilon \}$
and
![]() $f(\varepsilon ) \mathrel {\mathop :}= \varepsilon $
.
$f(\varepsilon ) \mathrel {\mathop :}= \varepsilon $
.
At step s, suppose we have defined a finite, completely branching binary tree
![]() $S \subseteq 2^{<\mathbb {N}}$
, and for every
$S \subseteq 2^{<\mathbb {N}}$
, and for every
![]() $\sigma \in S$
, a set
$\sigma \in S$
, a set
![]() $N^s_{\sigma } \subseteq T$
such that
$N^s_{\sigma } \subseteq T$
such that
![]() $\{N^s_{\sigma } : \sigma \in S\}$
forms a partition of T minus finitely many elements. Moreover, assume we have defined a mapping
$\{N^s_{\sigma } : \sigma \in S\}$
forms a partition of T minus finitely many elements. Moreover, assume we have defined a mapping
![]() $f : S \to T$
.
$f : S \to T$
.
Search for a split triple
![]() $(\mu , n_0, n_1)$
in
$(\mu , n_0, n_1)$
in
![]() $\bigcup _{\sigma \in S} N^s_{\sigma }$
. Let
$\bigcup _{\sigma \in S} N^s_{\sigma }$
. Let
![]() $\sigma \in S$
be such that
$\sigma \in S$
be such that
![]() $\mu \in N^s_{\sigma }$
. Let
$\mu \in N^s_{\sigma }$
. Let
![]() $\tau $
be any leaf of S such that
$\tau $
be any leaf of S such that
![]() $\tau \succeq \sigma $
(for example, pick the left-most successor of
$\tau \succeq \sigma $
(for example, pick the left-most successor of
![]() $\sigma $
). Add
$\sigma $
). Add
![]() $\tau \cdot 0$
and
$\tau \cdot 0$
and
![]() $\tau \cdot 1$
to S, and set
$\tau \cdot 1$
to S, and set
![]() $f(\tau \cdot i) = \mu \cdot n_i$
for each
$f(\tau \cdot i) = \mu \cdot n_i$
for each
![]() $i<2$
. Note that S is still completely branching.
$i<2$
. Note that S is still completely branching.
Then, split
![]() $N^s_{\sigma }$
into three disjoint subsets
$N^s_{\sigma }$
into three disjoint subsets
![]() $N^{s+1}_{\sigma }$
,
$N^{s+1}_{\sigma }$
,
![]() $N^{s+1}_{\tau \cdot 0}$
,
$N^{s+1}_{\tau \cdot 0}$
,
![]() $N^{s+1}_{\tau \cdot 1}$
as follows: (for
$N^{s+1}_{\tau \cdot 1}$
as follows: (for
![]() $i<2$
)
$i<2$
)
![]() $N^{s+1}_{\tau \cdot i}\mathrel {\mathop :}= \{\rho \in N^s_{\sigma } \mid \rho \succcurlyeq \mu \cdot n_i\}$
and
$N^{s+1}_{\tau \cdot i}\mathrel {\mathop :}= \{\rho \in N^s_{\sigma } \mid \rho \succcurlyeq \mu \cdot n_i\}$
and
![]() $N^{s+1}_{\sigma }\mathrel {\mathop :}= \{\rho \in N^s_{\tau } \mid \forall i<2, \rho \bot \mu \cdot n_i\}$
. Note that these sets do not form a partition of
$N^{s+1}_{\sigma }\mathrel {\mathop :}= \{\rho \in N^s_{\tau } \mid \forall i<2, \rho \bot \mu \cdot n_i\}$
. Note that these sets do not form a partition of
![]() $N^s_{\sigma }$
as we missed the nodes in
$N^s_{\sigma }$
as we missed the nodes in
![]() $\{\rho \in N^s_{\sigma } \mid \rho \preccurlyeq \mu \}$
, fortunately there are only finitely many of them. Lastly, set
$\{\rho \in N^s_{\sigma } \mid \rho \preccurlyeq \mu \}$
, fortunately there are only finitely many of them. Lastly, set
![]() $N^{s+1}_{\nu }\mathrel {\mathop :}= N^s_{\nu }$
for every
$N^{s+1}_{\nu }\mathrel {\mathop :}= N^s_{\nu }$
for every
![]() $\nu \in S - \{\sigma , \tau \cdot 0, \tau \cdot 1 \}$
.
$\nu \in S - \{\sigma , \tau \cdot 0, \tau \cdot 1 \}$
.
Verification. First, let us prove that at any step s,
![]() $\bigcup _{\sigma \in S} N^s_{\sigma }$
contains infinitely many split triples, which ensures that the search always terminates. Note that
$\bigcup _{\sigma \in S} N^s_{\sigma }$
contains infinitely many split triples, which ensures that the search always terminates. Note that
![]() $T-\bigcup _{\sigma \in S} N^s_{\sigma }$
is a c.e. subset of
$T-\bigcup _{\sigma \in S} N^s_{\sigma }$
is a c.e. subset of
![]() $\bigcup _{\sigma \in S} \{\rho \mid \rho \preceq \sigma \}$
, hence exists by bounded
$\bigcup _{\sigma \in S} \{\rho \mid \rho \preceq \sigma \}$
, hence exists by bounded
![]() $\Sigma _1$
comprehension, which follows from
$\Sigma _1$
comprehension, which follows from
![]() $\mathsf {RCA}_0$
. Moreover, by assumption, T is a finitely branching c.e. tree, which means that every
$\mathsf {RCA}_0$
. Moreover, by assumption, T is a finitely branching c.e. tree, which means that every
![]() $\rho \in T-\bigcup _{\sigma \in S} N^s_{\sigma }$
belongs to a bounded number of split triples of T. By
$\rho \in T-\bigcup _{\sigma \in S} N^s_{\sigma }$
belongs to a bounded number of split triples of T. By
![]() $\mathsf {B}\Sigma ^0_1$
(which follows from
$\mathsf {B}\Sigma ^0_1$
(which follows from
![]() $\mathsf {RCA}_0$
), the number of split triples in T which involve a node from
$\mathsf {RCA}_0$
), the number of split triples in T which involve a node from
![]() $T-\bigcup _{\sigma \in S} N^s_{\sigma }$
is bounded. Since by assumption, T contains infinitely many split triples,
$T-\bigcup _{\sigma \in S} N^s_{\sigma }$
is bounded. Since by assumption, T contains infinitely many split triples,
![]() $T-\bigcup _{\sigma \in S} N^s_{\sigma }$
must contain infinitely many of them.
$T-\bigcup _{\sigma \in S} N^s_{\sigma }$
must contain infinitely many of them.
Second, we prove by induction on s that
![]() $\forall s\in \mathbb {N}, \forall \sigma \neq \nu \in S, N_{\sigma }^s\bot N_{\nu }^s$
, i.e.,
$\forall s\in \mathbb {N}, \forall \sigma \neq \nu \in S, N_{\sigma }^s\bot N_{\nu }^s$
, i.e.,
![]() $\forall \mu \in N_{\sigma }^s, \forall \rho \in N_{\nu }^s, \mu \bot \rho $
. At step 0, the assertion is trivially verified. At step s, suppose we found the split triple
$\forall \mu \in N_{\sigma }^s, \forall \rho \in N_{\nu }^s, \mu \bot \rho $
. At step 0, the assertion is trivially verified. At step s, suppose we found the split triple
![]() $(\mu , n_0, n_1)$
in the set
$(\mu , n_0, n_1)$
in the set
![]() $N_{\sigma }^s$
, and that
$N_{\sigma }^s$
, and that
![]() $\forall i<2, f(\tau \cdot i)=\mu \cdot n_i$
where
$\forall i<2, f(\tau \cdot i)=\mu \cdot n_i$
where
![]() $\tau \succcurlyeq \sigma $
. Since
$\tau \succcurlyeq \sigma $
. Since
![]() $\mu $
was found in
$\mu $
was found in
![]() $N_{\sigma }^s$
, the latter is split into
$N_{\sigma }^s$
, the latter is split into
![]() $N_{\tau \cdot 0}^{s+1}$
,
$N_{\tau \cdot 0}^{s+1}$
,
![]() $N_{\tau \cdot 1}^{s+1}$
and
$N_{\tau \cdot 1}^{s+1}$
and
![]() $N_{\sigma }^{s+1}$
, the other sets remain identical. By construction, and because they are all subsets of
$N_{\sigma }^{s+1}$
, the other sets remain identical. By construction, and because they are all subsets of
![]() $N_{\sigma }^s$
, the assertion holds.
$N_{\sigma }^s$
, the assertion holds.
We now prove (*), consider
![]() $\sigma , \nu \in S$
such that
$\sigma , \nu \in S$
such that
![]() $\sigma \bot \nu $
. WLOG suppose
$\sigma \bot \nu $
. WLOG suppose
![]() $\nu $
was added to S sooner than
$\nu $
was added to S sooner than
![]() $\sigma $
, more precisely
$\sigma $
, more precisely
![]() $f(\nu )$
appeared (as child in a split triple) at step s in some set
$f(\nu )$
appeared (as child in a split triple) at step s in some set
![]() $N_{-}^s$
, so
$N_{-}^s$
, so
![]() $N_{\nu }^{s+1}$
contains
$N_{\nu }^{s+1}$
contains
![]() $f(\nu )$
by construction. Since
$f(\nu )$
by construction. Since
![]() $\sigma $
was added to S after
$\sigma $
was added to S after
![]() $\nu $
, there exists
$\nu $
, there exists
![]() $\rho \in S$
such that
$\rho \in S$
such that
![]() $f(\sigma )\in N_{\rho }^{s+1}$
. By contradiction
$f(\sigma )\in N_{\rho }^{s+1}$
. By contradiction
![]() $\rho \neq \sigma $
holds, as otherwise
$\rho \neq \sigma $
holds, as otherwise
![]() $f(\sigma )\in N_{\tau }^{s+1}$
, and so
$f(\sigma )\in N_{\tau }^{s+1}$
, and so
![]() $\sigma $
would extend
$\sigma $
would extend
![]() $\tau $
by construction of S. Thus by using the previous assertion, we deduce
$\tau $
by construction of S. Thus by using the previous assertion, we deduce
![]() $f(\sigma )\bot f(\nu )$
.
$f(\sigma )\bot f(\nu )$
.
Proposition 2.9.
![]() $\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ trees}} \implies {\mathsf {CAC\ for\ c.e.\ trees}}$
and
$\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ trees}} \implies {\mathsf {CAC\ for\ c.e.\ trees}}$
and
![]() ${\mathsf {CAC\ for\ c.e.\ trees}}\leqslant _c{\mathsf {CAC\ for\ trees}}$
.
${\mathsf {CAC\ for\ c.e.\ trees}}\leqslant _c{\mathsf {CAC\ for\ trees}}$
.
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be a c.e. tree. We define the computable tree
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be a c.e. tree. We define the computable tree
![]() $S\subseteq \mathbb {N}^{<\mathbb {N}}$
by
$S\subseteq \mathbb {N}^{<\mathbb {N}}$
by
![]() $\langle n_0, s_0\rangle \cdot \ldots \cdot \langle n_{k-1}, s_{k-1}\rangle \in S$
if and only if for all
$\langle n_0, s_0\rangle \cdot \ldots \cdot \langle n_{k-1}, s_{k-1}\rangle \in S$
if and only if for all
![]() $j<k$
,
$j<k$
,
![]() $s_j$
is the smallest integer such that
$s_j$
is the smallest integer such that
![]() $n_0\cdot \ldots \cdot n_j\in T[s_j]$
, where
$n_0\cdot \ldots \cdot n_j\in T[s_j]$
, where
![]() $T[s_j]$
is the approximation of T at stage
$T[s_j]$
is the approximation of T at stage
![]() $s_j$
.
$s_j$
.
By
![]() ${\mathsf {CAC\ for\ trees}}$
, there is an infinite chain (resp. antichain) in S, and by forgetting the second component of each string, we obtain an infinite chain (resp. antichain) in T.
${\mathsf {CAC\ for\ trees}}$
, there is an infinite chain (resp. antichain) in S, and by forgetting the second component of each string, we obtain an infinite chain (resp. antichain) in T.
Before finishing this section, we introduce a set version of the principle
![]() $\mathsf {TAC}$
, which is more convenient to manipulate than
$\mathsf {TAC}$
, which is more convenient to manipulate than
![]() $\mathsf {TAC}$
. Indeed, when working with
$\mathsf {TAC}$
. Indeed, when working with
![]() $\mathsf {TAC}$
, the downward-closure of the tree is not relevant, and we naturally end up taking an infinite computable subset of the tree rather than working with the c.e. tree. This motivates the following definitions.
$\mathsf {TAC}$
, the downward-closure of the tree is not relevant, and we naturally end up taking an infinite computable subset of the tree rather than working with the c.e. tree. This motivates the following definitions.
Definition 2.10. A set
![]() $X \subseteq 2^{<\mathbb {N}}$
is completely branching if for every
$X \subseteq 2^{<\mathbb {N}}$
is completely branching if for every
![]() $\sigma \in 2^{<\mathbb {N}}$
,
$\sigma \in 2^{<\mathbb {N}}$
,
![]() $\sigma \cdot 0 \in X$
iff
$\sigma \cdot 0 \in X$
iff
![]() $\sigma \cdot 1 \in X$
.
$\sigma \cdot 1 \in X$
.
Note that the above definition is compatible with the notion of completely branching tree.
Definition 2.11 (
 $\mathsf {SAC}$
, set antichain theorem)
$\mathsf {SAC}$
, set antichain theorem)
Every infinite completely branching set
![]() $X \subseteq 2^{<\mathbb {N}}$
has an infinite antichain.
$X \subseteq 2^{<\mathbb {N}}$
has an infinite antichain.
The set antichain theorem is equivalent to the tree antichain theorem, as shows the following lemma.
Lemma 2.12.
![]() $\mathsf {RCA}_0 \vdash \mathsf {SAC} \iff \mathsf {TAC}$
.
$\mathsf {RCA}_0 \vdash \mathsf {SAC} \iff \mathsf {TAC}$
.
Proof
![]() $\mathsf {SAC} \implies \mathsf {TAC}$
. Let
$\mathsf {SAC} \implies \mathsf {TAC}$
. Let
![]() $T \subseteq 2^{<\mathbb {N}}$
be an infinite, completely branching c.e. tree. Let
$T \subseteq 2^{<\mathbb {N}}$
be an infinite, completely branching c.e. tree. Let
![]() $S \subseteq T$
be an infinite computable, completely branching set. By
$S \subseteq T$
be an infinite computable, completely branching set. By
![]() $\mathsf {SAC}$
, there is an infinite antichain
$\mathsf {SAC}$
, there is an infinite antichain
![]() $A \subseteq X$
. In particular, A is an antichain for T.
$A \subseteq X$
. In particular, A is an antichain for T.
![]() $\mathsf {SAC} \impliedby \mathsf {TAC}$
. Let
$\mathsf {SAC} \impliedby \mathsf {TAC}$
. Let
![]() $S \subseteq 2^{<\mathbb {N}}$
be an infinite computable, completely branching set. One can define an infinite computable tree
$S \subseteq 2^{<\mathbb {N}}$
be an infinite computable, completely branching set. One can define an infinite computable tree
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
by letting
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
by letting
![]() $\sigma \in T$
iff for every
$\sigma \in T$
iff for every
![]() $n < |\sigma |$
,
$n < |\sigma |$
,
![]() $\sigma (n)$
codes for a binary string
$\sigma (n)$
codes for a binary string
![]() $\tau _n \in S$
, such that for every
$\tau _n \in S$
, such that for every
![]() $n < |\sigma |-1$
,
$n < |\sigma |-1$
,
![]() $\tau _{n} \prec \tau _{n+1}$
, and there is no string in S strictly between
$\tau _{n} \prec \tau _{n+1}$
, and there is no string in S strictly between
![]() $\tau _n$
and
$\tau _n$
and
![]() $\tau _{n+1}$
. The tree T is such that every chain in T codes for a chain in S, and every antichain in T codes for an antichain in S. We can see T as an instance of
$\tau _{n+1}$
. The tree T is such that every chain in T codes for a chain in S, and every antichain in T codes for an antichain in S. We can see T as an instance of
![]() ${\mathsf {CAC\ for\ trees}}$
. Moreover, since S is completely branching, then T has infinitely many split triples, so the proof of Proposition 2.8 applied to this instance T of
${\mathsf {CAC\ for\ trees}}$
. Moreover, since S is completely branching, then T has infinitely many split triples, so the proof of Proposition 2.8 applied to this instance T of
![]() ${\mathsf {CAC\ for\ trees}}$
does not use
${\mathsf {CAC\ for\ trees}}$
does not use
![]() $\mathsf {B}\Sigma ^0_2$
. Thus there is either an infinite chain for T, or an infinite antichain for S. With the appropriate decoding, we obtain an infinite antichain for S.
$\mathsf {B}\Sigma ^0_2$
. Thus there is either an infinite chain for T, or an infinite antichain for S. With the appropriate decoding, we obtain an infinite antichain for S.
3 Probabilistic proofs of
 $\mathsf {SAC}$
$\mathsf {SAC}$
The restriction of
![]() $\mathsf {CAC}$
to trees yields a strictly weaker statement from the viewpoint the arithmetical bounds in the arithmetic hierarchy. Indeed, by Herrmann [Reference Herrmann11, Theorem 3.1], there is a computable partial order with no
$\mathsf {CAC}$
to trees yields a strictly weaker statement from the viewpoint the arithmetical bounds in the arithmetic hierarchy. Indeed, by Herrmann [Reference Herrmann11, Theorem 3.1], there is a computable partial order with no
![]() $\Delta ^0_2$
infinite chain or antichain, while by Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.2], every infinite computable tree must have either an infinite computable chain or an infinite
$\Delta ^0_2$
infinite chain or antichain, while by Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.2], every infinite computable tree must have either an infinite computable chain or an infinite
![]() $\Pi _1^0$
antichain. In this section, we go one step further in the study of the weakness of
$\Pi _1^0$
antichain. In this section, we go one step further in the study of the weakness of
![]() ${\mathsf {CAC\ for\ trees}}$
by proving that
${\mathsf {CAC\ for\ trees}}$
by proving that
![]() $\mathsf {SAC}$
admits probabilistic solutions. Before this, we prove two technical lemmas.
$\mathsf {SAC}$
admits probabilistic solutions. Before this, we prove two technical lemmas.
Lemma 3.1 (
 $\mathsf {RCA}_0$
)
$\mathsf {RCA}_0$
)
Let
![]() $S \subseteq 2^{<\mathbb {N}}$
be an infinite completely branching set. Then for every n, there exists an antichain of size n.
$S \subseteq 2^{<\mathbb {N}}$
be an infinite completely branching set. Then for every n, there exists an antichain of size n.
Proof By finite Ramsey’s theorem for pairs and two colors (which holds in
![]() $\mathsf {RCA}_0$
), there exists some
$\mathsf {RCA}_0$
), there exists some
![]() $p \in \mathbb {N}$
such that for every 2-coloring of
$p \in \mathbb {N}$
such that for every 2-coloring of
![]() $[p]^2$
, there exists a homogeneous set of size n. Since S is infinite, there exists a subset
$[p]^2$
, there exists a homogeneous set of size n. Since S is infinite, there exists a subset
![]() $P \subseteq S$
of size p. By choice of p, there exists a subset
$P \subseteq S$
of size p. By choice of p, there exists a subset
![]() $Q \subseteq P$
of size n such that either Q is a chain, or an antichain. In the latter case, we are done. In the former case, since S is completely branching, the set
$Q \subseteq P$
of size n such that either Q is a chain, or an antichain. In the latter case, we are done. In the former case, since S is completely branching, the set
![]() $\{\hat {\sigma }\mid \sigma \in Q \} \subseteq S$
is an antichain, where
$\{\hat {\sigma }\mid \sigma \in Q \} \subseteq S$
is an antichain, where
![]() $\hat {\sigma }$
is the string obtained from
$\hat {\sigma }$
is the string obtained from
![]() $\sigma $
by flipping its last bit.
$\sigma $
by flipping its last bit.
Lemma 3.2 (
 $\mathsf {RCA}_0$
)
$\mathsf {RCA}_0$
)
Let
![]() $S \subseteq 2^{<\mathbb {N}}$
be an infinite completely branching set. Then for every antichain
$S \subseteq 2^{<\mathbb {N}}$
be an infinite completely branching set. Then for every antichain
![]() $A \subseteq S$
, for all but at most one
$A \subseteq S$
, for all but at most one
![]() $\sigma \in A$
, the set
$\sigma \in A$
, the set
![]() $S_{\sigma } \mathrel {\mathop :}= \{ \tau \in S\mid \sigma \bot \tau \mbox { and } |\tau |> |\sigma | \}$
is infinite and completely branching.
$S_{\sigma } \mathrel {\mathop :}= \{ \tau \in S\mid \sigma \bot \tau \mbox { and } |\tau |> |\sigma | \}$
is infinite and completely branching.
Proof First, since
![]() $S \subseteq 2^{<\mathbb {N}}$
completely branching, then for every
$S \subseteq 2^{<\mathbb {N}}$
completely branching, then for every
![]() $\sigma \in 2^{<\mathbb {N}}$
, the set
$\sigma \in 2^{<\mathbb {N}}$
, the set
![]() $S_{\sigma }$
is completely branching. Suppose for the sake of contradiction that there exists two strings
$S_{\sigma }$
is completely branching. Suppose for the sake of contradiction that there exists two strings
![]() $\sigma , \rho \in A$
such that
$\sigma , \rho \in A$
such that
![]() $S_{\sigma }$
and
$S_{\sigma }$
and
![]() $S_{\rho }$
are both finite. Then pick any
$S_{\rho }$
are both finite. Then pick any
![]() $\tau \in S - (S_{\sigma } \cup S_{\rho })$
with
$\tau \in S - (S_{\sigma } \cup S_{\rho })$
with
![]() $|\tau |> \max (|\sigma |, |\rho |)$
. It follows that
$|\tau |> \max (|\sigma |, |\rho |)$
. It follows that
![]() $\sigma \prec \tau $
and
$\sigma \prec \tau $
and
![]() $\rho \prec \tau $
, and thus that
$\rho \prec \tau $
, and thus that
![]() $\sigma $
and
$\sigma $
and
![]() $\rho $
are comparable, contradicting the fact that A is an antichain.
$\rho $
are comparable, contradicting the fact that A is an antichain.
Proposition 3.3. The measure of the oracles computing a solution for a computable instance of
![]() $\mathsf {SAC}$
is 1.
$\mathsf {SAC}$
is 1.
Remark 3.4. The proof of the above proposition is carried out purely as a computability statement, hence we have access to as much induction as needed.
Proof Let
![]() $S \subseteq 2^{<\mathbb {N}}$
be an infinite computably branching set. We are going to build a decreasing sequence of infinite completely branching sets of strings
$S \subseteq 2^{<\mathbb {N}}$
be an infinite computably branching set. We are going to build a decreasing sequence of infinite completely branching sets of strings
![]() $S_0 \supseteq S_1 \supseteq \dots $
, with
$S_0 \supseteq S_1 \supseteq \dots $
, with
![]() $S_0\mathrel {\mathop :}= S$
, together with finite antichains
$S_0\mathrel {\mathop :}= S$
, together with finite antichains
![]() $A_i\subseteq S_i$
(for
$A_i\subseteq S_i$
(for
![]() $i\in \mathbb {N}$
), in order to have an infinite antichain
$i\in \mathbb {N}$
), in order to have an infinite antichain
![]() $A\mathrel {\mathop :}=\{\sigma _i\mid i\in \mathbb {N}\}$
where
$A\mathrel {\mathop :}=\{\sigma _i\mid i\in \mathbb {N}\}$
where
![]() $\sigma _i\in A_i$
.
$\sigma _i\in A_i$
.
This construction will work with positive probability, and since the class of oracles computing a solution to the instance S is invariant under Turing equivalence, this implies that this class has measure 1. Indeed, by Kolmogorov’s 0-1 law, every measurable Turing-invariant class has either measure 0 or 1.
First, let
![]() $S_0\mathrel {\mathop :}= S$
. At step k, assume the sets
$S_0\mathrel {\mathop :}= S$
. At step k, assume the sets
![]() $S_0 \supseteq S_1\supseteq \cdots \supseteq S_k$
and
$S_0 \supseteq S_1\supseteq \cdots \supseteq S_k$
and
![]() $A_0, \ldots , A_{k-1}$
have been defined, as well as the finite antichain
$A_0, \ldots , A_{k-1}$
have been defined, as well as the finite antichain
![]() $\{\sigma _0, \ldots , \sigma _{k-1}\}$
, such that
$\{\sigma _0, \ldots , \sigma _{k-1}\}$
, such that
![]() $\forall \tau \in S_k, \forall i<k, \sigma _i\bot \tau $
.
$\forall \tau \in S_k, \forall i<k, \sigma _i\bot \tau $
.
Search computably for a finite antichain
![]() $A_k\subseteq S_k$
of size
$A_k\subseteq S_k$
of size
![]() $2^{k+2}$
. If found, pick an element
$2^{k+2}$
. If found, pick an element
![]() $\sigma _k\in A_k$
at random. Then define
$\sigma _k\in A_k$
at random. Then define
![]() $S_{k+1}\mathrel {\mathop :}= \{\tau \in S_k\mid \sigma _k\bot \tau \mbox { and } |\tau |> |\sigma _k| \}$
for the next step.
$S_{k+1}\mathrel {\mathop :}= \{\tau \in S_k\mid \sigma _k\bot \tau \mbox { and } |\tau |> |\sigma _k| \}$
for the next step.
If the procedure never stops, it yields an infinite antichain
![]() $A\mathrel {\mathop :}= \{\sigma _i\mid i\in \mathbb {N}\}$
thanks to the definition of the sets
$A\mathrel {\mathop :}= \{\sigma _i\mid i\in \mathbb {N}\}$
thanks to the definition of the sets
![]() $(S_i)_{i<k}$
. Assuming that
$(S_i)_{i<k}$
. Assuming that
![]() $S_k$
is an infinite completely branching set, Lemma 3.1 ensures that
$S_k$
is an infinite completely branching set, Lemma 3.1 ensures that
![]() $A_k$
will be found.
$A_k$
will be found.
However, if at any point,
![]() $S_k$
is not an infinite completely branching set, then at some point t we will not be able to find a large enough
$S_k$
is not an infinite completely branching set, then at some point t we will not be able to find a large enough
![]() $A_t$
in it. If this happens, since
$A_t$
in it. If this happens, since
![]() $S_{k+1}$
is completely determined by
$S_{k+1}$
is completely determined by
![]() $S_k$
and
$S_k$
and
![]() $\sigma _k$
, it means that we have chosen some “bad”
$\sigma _k$
, it means that we have chosen some “bad”
![]() $\sigma _k \in A_k$
. Luckily, by Lemma 3.2, there is at most one element of this kind in
$\sigma _k \in A_k$
. Luckily, by Lemma 3.2, there is at most one element of this kind in
![]() $A_k$
. Thus, if we pick
$A_k$
. Thus, if we pick
![]() $\sigma _k$
at random in
$\sigma _k$
at random in
![]() $A_k$
, we have at most
$A_k$
, we have at most
![]() $\frac {1}{|A_k|}=\frac {1}{2^{k+2}}$
chances for this case to happen. So the overall probability that this procedure fails is less than
$\frac {1}{|A_k|}=\frac {1}{2^{k+2}}$
chances for this case to happen. So the overall probability that this procedure fails is less than
![]() $\sum _{k\geqslant 0} \frac {1}{2^{k+2}}=\frac {1}{2}$
. Hence we found an antichain with positive probability.
$\sum _{k\geqslant 0} \frac {1}{2^{k+2}}=\frac {1}{2}$
. Hence we found an antichain with positive probability.
Very few theorems studied in reverse mathematics admit a probabilistic proof. Proposition 3.3 provides a powerful method for separating the statement
![]() ${\mathsf {CAC\ for\ trees}}$
from many theorems in reverse mathematics. In what follows,
${\mathsf {CAC\ for\ trees}}$
from many theorems in reverse mathematics. In what follows,
![]() $\mathsf {AMT}$
stands for the Atomic Model Theorem, studied by Hirschfeldt, Shore, and Slaman [Reference Hirschfeldt, Shore and Slaman14],
$\mathsf {AMT}$
stands for the Atomic Model Theorem, studied by Hirschfeldt, Shore, and Slaman [Reference Hirschfeldt, Shore and Slaman14],
![]() $\mathsf {COH}$
is the cohesiveness principle, defined by Cholak, Jockusch, and Slaman [Reference Cholak, Jockusch and Slaman4, Statement 7.7], and
$\mathsf {COH}$
is the cohesiveness principle, defined by Cholak, Jockusch, and Slaman [Reference Cholak, Jockusch and Slaman4, Statement 7.7], and
![]() $\mathsf {RWKL}$
is the Ramsey-type Weak König’s lemma, defined by Flood [Reference Flood10, Statement 2] under the name
$\mathsf {RWKL}$
is the Ramsey-type Weak König’s lemma, defined by Flood [Reference Flood10, Statement 2] under the name
![]() $\mathsf {RKL}$
.
$\mathsf {RKL}$
.
Corollary 3.5. Over
![]() $\mathsf {RCA}_0$
,
$\mathsf {RCA}_0$
,
![]() ${\mathsf {CAC\ for\ trees}}$
implies none of
${\mathsf {CAC\ for\ trees}}$
implies none of
![]() $\kern1pt\mathsf {AMT}$
,
$\kern1pt\mathsf {AMT}$
,
![]() $\mathsf {COH}$
, and
$\mathsf {COH}$
, and
![]() $\mathsf {RWKL}$
.
$\mathsf {RWKL}$
.
Proof These three statements have a computable instance such that the measure of the oracles computing a solution is 0 (see [Reference Astor, Bienvenu, Dzhafarov, Patey, Shafer, Solomon and Westrick1]).
The argument of Proposition 3.3 can be formalized over
![]() $\mathsf {RCA}_0$
to yield the following result.
$\mathsf {RCA}_0$
to yield the following result.
Definition 3.6 (
 $2\mbox {-}\mathsf {RAN}$
)
$2\mbox {-}\mathsf {RAN}$
)
For every sequence of uniformly
![]() $\Pi ^0_2$
binary trees
$\Pi ^0_2$
binary trees
![]() $T_0, T_1,\ldots $
such that, for every n,
$T_0, T_1,\ldots $
such that, for every n,
![]() $\mu ([T_n])> 1-2^{-n}$
, there is some n and some set X such that
$\mu ([T_n])> 1-2^{-n}$
, there is some n and some set X such that
![]() $X \in [T_n]$
.
$X \in [T_n]$
.
Proposition 3.7.
![]() $\mathsf {RCA}_0 \vdash 2\mbox {-}\mathsf {RAN} \implies \mathsf {SAC}$
.
$\mathsf {RCA}_0 \vdash 2\mbox {-}\mathsf {RAN} \implies \mathsf {SAC}$
.
Proof For every n, consider the construction of Proposition 3.3, where the antichain
![]() $A_k$
is of size
$A_k$
is of size
![]() $2^{n+k+1}$
instead of
$2^{n+k+1}$
instead of
![]() $2^{k+2}$
. For each k, let
$2^{k+2}$
. For each k, let
![]() $\sigma _k \in A_k$
be the unique “bad” choice (if it exists), that is, which makes the set
$\sigma _k \in A_k$
be the unique “bad” choice (if it exists), that is, which makes the set
![]() $S_{k+1}$
finite, and let
$S_{k+1}$
finite, and let
![]() $\tau _k$
be the string of length
$\tau _k$
be the string of length
![]() $n+k+1$
corresponding to the binary representation of the rank of
$n+k+1$
corresponding to the binary representation of the rank of
![]() $\sigma _k$
in
$\sigma _k$
in
![]() $A_k$
for some fixed order on binary strings. Then one can compute
$A_k$
for some fixed order on binary strings. Then one can compute
![]() $\sigma _k$
from
$\sigma _k$
from
![]() $\tau _k$
and the finite set
$\tau _k$
and the finite set
![]() $A_k$
. Note that
$A_k$
. Note that
![]() $\tau _k$
is undefined when
$\tau _k$
is undefined when
![]() $\sigma _k$
does not exist.
$\sigma _k$
does not exist.
Consider the
![]() $\Sigma ^0_2$
class
$\Sigma ^0_2$
class
![]() $\mathcal {U}_n \mathrel {\mathop :}= \{ X \in 2^{\mathbb {N}}\mid \exists k, \tau _k \prec X \}=\bigcup _k [\tau _k]$
. It verifies
$\mathcal {U}_n \mathrel {\mathop :}= \{ X \in 2^{\mathbb {N}}\mid \exists k, \tau _k \prec X \}=\bigcup _k [\tau _k]$
. It verifies
 $$ \begin{align*}\mu(\mathcal{U}_n) \leqslant \sum_{{k \geqslant 0}\atop {\sigma_k \text{exists}}} \mu\big([\tau_k]\big) \leqslant \sum_{k \geqslant 0} \frac{1}{2^{n+k+1}} = 2^{-n}.\end{align*} $$
$$ \begin{align*}\mu(\mathcal{U}_n) \leqslant \sum_{{k \geqslant 0}\atop {\sigma_k \text{exists}}} \mu\big([\tau_k]\big) \leqslant \sum_{k \geqslant 0} \frac{1}{2^{n+k+1}} = 2^{-n}.\end{align*} $$
Let
![]() $T_n$
be a
$T_n$
be a
![]() $\Pi ^0_2$
tree such that
$\Pi ^0_2$
tree such that
![]() $[T_n] = 2^{\mathbb {N}} - \mathcal {U}_n$
. We can now consider the sequence of trees
$[T_n] = 2^{\mathbb {N}} - \mathcal {U}_n$
. We can now consider the sequence of trees
![]() $(T_n)_{n\in \mathbb {N}}$
. By
$(T_n)_{n\in \mathbb {N}}$
. By
![]() $2\mbox {-}\mathsf {RAN}$
, there is some n and some
$2\mbox {-}\mathsf {RAN}$
, there is some n and some
![]() $X \in [T_n]$
. For any instance of
$X \in [T_n]$
. For any instance of
![]() $\mathsf {SAC}$
, find a solution by running the construction given in Proposition 3.3 with the help of X to avoid the potential “bad” choice in each
$\mathsf {SAC}$
, find a solution by running the construction given in Proposition 3.3 with the help of X to avoid the potential “bad” choice in each
![]() $A_k$
.
$A_k$
.
Corollary 3.8. Over
![]() $\mathsf {RCA}_0$
,
$\mathsf {RCA}_0$
,
![]() $\mathsf {SAC}$
(and therefore
$\mathsf {SAC}$
(and therefore
![]() $\mathsf {TAC}$
) implies none of
$\mathsf {TAC}$
) implies none of
![]() $\mathsf {B}\Sigma ^0_2$
and
$\mathsf {B}\Sigma ^0_2$
and
![]() ${\mathsf {CAC\ for\ trees}}$
.
${\mathsf {CAC\ for\ trees}}$
.
Proof Slaman [unpublished] proved that
![]() $2\mbox {-}\mathsf {RAN}$
does not imply
$2\mbox {-}\mathsf {RAN}$
does not imply
![]() $\mathsf {B}\Sigma ^0_2$
over
$\mathsf {B}\Sigma ^0_2$
over
![]() $\mathsf {RCA}_0$
. The result can also be found in [Reference Belanger, Chong, Li, Wang and Yang2]. The corollary follows from
$\mathsf {RCA}_0$
. The result can also be found in [Reference Belanger, Chong, Li, Wang and Yang2]. The corollary follows from
![]() $\mathsf {RCA}_0 \vdash \mathsf {SAC} \implies \mathsf {TAC}$
(Lemma 2.12) and
$\mathsf {RCA}_0 \vdash \mathsf {SAC} \implies \mathsf {TAC}$
(Lemma 2.12) and
![]() $\mathsf {RCA}_0 \vdash \mathsf {TAC}+\mathsf {B}\Sigma ^0_2 \iff {\mathsf {CAC\ for\ trees}}$
(Theorem 2.5).
$\mathsf {RCA}_0 \vdash \mathsf {TAC}+\mathsf {B}\Sigma ^0_2 \iff {\mathsf {CAC\ for\ trees}}$
(Theorem 2.5).
We are now going to refine Proposition 3.3 by proving that some variant of
![]() $\mathsf {DNC}$
is sufficient to compute a solution of
$\mathsf {DNC}$
is sufficient to compute a solution of
![]() $\mathsf {SAC}$
.
$\mathsf {SAC}$
.
Definition 3.9 (Diagonally non-computable function)
A function
![]() $f : \mathbb {N} \to \mathbb {N}$
is diagonally non-computable relative to X (or
$f : \mathbb {N} \to \mathbb {N}$
is diagonally non-computable relative to X (or
![]() $\mathsf {DNC}(X)$
) if for every e,
$\mathsf {DNC}(X)$
) if for every e,
![]() $f(e) \neq \Phi ^X_e(e)$
. Whenever f is dominated by a function
$f(e) \neq \Phi ^X_e(e)$
. Whenever f is dominated by a function
![]() $h : \mathbb {N} \to \mathbb {N}$
, then we say that f is
$h : \mathbb {N} \to \mathbb {N}$
, then we say that f is
![]() $\mathsf {DNC}_h(X)$
. A Turing degree is
$\mathsf {DNC}_h(X)$
. A Turing degree is
![]() $\mathsf {DNC}_h(X)$
if it contains a
$\mathsf {DNC}_h(X)$
if it contains a
![]() $\mathsf {DNC}_h(X)$
function.
$\mathsf {DNC}_h(X)$
function.
The following lemma gives a much more convenient way to work with
![]() $\mathsf {DNC}_h(X)$
functions.
$\mathsf {DNC}_h(X)$
functions.
Lemma 3.10 (Folklore)
Let
![]() $A, X$
be subsets of
$A, X$
be subsets of
![]() $\mathbb {N}$
. The following are equivalent:
$\mathbb {N}$
. The following are equivalent:
-
(1) A is of degree
 $\mathsf {DNC}_h(X)$
for some computable (primitive recursive) function
$\mathsf {DNC}_h(X)$
for some computable (primitive recursive) function
 $h:\mathbb {N}\to \mathbb {N}$
.
$h:\mathbb {N}\to \mathbb {N}$
. -
(2) A computes a function
 $g:\mathbb {N}^2\to \mathbb {N}$
such that and which is dominated by a computable function
$g:\mathbb {N}^2\to \mathbb {N}$
such that and which is dominated by a computable function $$ \begin{align*}\forall e, n, |W_e^X|\leqslant n\implies g(e, n)\notin W_e^X\end{align*} $$
$$ \begin{align*}\forall e, n, |W_e^X|\leqslant n\implies g(e, n)\notin W_e^X\end{align*} $$
 $b:\mathbb {N}^2\to \mathbb {N}$
, i.e.,
$b:\mathbb {N}^2\to \mathbb {N}$
, i.e.,  $$ \begin{align*}\forall e, n, g(e, n)<b(e, n).\end{align*} $$
$$ \begin{align*}\forall e, n, g(e, n)<b(e, n).\end{align*} $$
Proof
![]() $(2)\implies (1)$
. Let
$(2)\implies (1)$
. Let
![]() $i:\mathbb {N}\to \mathbb {N}$
be a computable (primitive recursive) function such that for any
$i:\mathbb {N}\to \mathbb {N}$
be a computable (primitive recursive) function such that for any
![]() $e\in \mathbb {N}$
and
$e\in \mathbb {N}$
and
![]() $B\subseteq \mathbb {N}$
we have
$B\subseteq \mathbb {N}$
we have
![]() $\Phi ^B_{i(e)}(x)\downarrow \iff x=\Phi _e^B(e)$
. Thus,
$\Phi ^B_{i(e)}(x)\downarrow \iff x=\Phi _e^B(e)$
. Thus,
 $$\begin{align*}W_{i(e)}^B=\begin{cases} \{\Phi_e^B(e)\},&\text{if }e\in B',\\ \varnothing,&\text{otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}W_{i(e)}^B=\begin{cases} \{\Phi_e^B(e)\},&\text{if }e\in B',\\ \varnothing,&\text{otherwise.} \end{cases}\end{align*}$$
From there, define the A-computable function
![]() $f:\mathbb {N}\to \mathbb {N}$
by
$f:\mathbb {N}\to \mathbb {N}$
by
![]() $f:e\mapsto g(i(e), 1)$
. It is
$f:e\mapsto g(i(e), 1)$
. It is
![]() $\mathsf {DNC}(X)$
because
$\mathsf {DNC}(X)$
because
![]() $g(i(e), 1)\notin W_{i(e)}^X$
since
$g(i(e), 1)\notin W_{i(e)}^X$
since
![]() $|W_{i(e)}^X|\leqslant 1$
. Moreover, f is dominated by the computable function
$|W_{i(e)}^X|\leqslant 1$
. Moreover, f is dominated by the computable function
![]() $e\mapsto b(i(e), 1)$
, because b computably dominates g.
$e\mapsto b(i(e), 1)$
, because b computably dominates g.
![]() $(1)\implies (2)$
. Let f be a
$(1)\implies (2)$
. Let f be a
![]() $\mathsf {DNC}_h(X)$
function computed by A. Given the pair
$\mathsf {DNC}_h(X)$
function computed by A. Given the pair
![]() $e, n$
, we describe the process that defines
$e, n$
, we describe the process that defines
![]() $g(e, n)$
.
$g(e, n)$
.
Construction. For each
![]() $i<n$
, we compute the code
$i<n$
, we compute the code
![]() $u(e, i)$
of the X-computable function which, on any input, looks for the
$u(e, i)$
of the X-computable function which, on any input, looks for the
![]() $i{\text {th}}$
element of
$i{\text {th}}$
element of
![]() $W_e^{X}$
. If it finds such an element, then it interprets it as an n-tuple
$W_e^{X}$
. If it finds such an element, then it interprets it as an n-tuple
![]() $\langle k_0, \ldots , k_{n-1}\rangle $
and returns the value
$\langle k_0, \ldots , k_{n-1}\rangle $
and returns the value
![]() $k_i$
. If it never finds such an element, then the function diverges. Finally we define
$k_i$
. If it never finds such an element, then the function diverges. Finally we define
![]() $g:e, n\mapsto \langle f(u(e, 0)), \ldots , f(u(e, n-1))\rangle .$
$g:e, n\mapsto \langle f(u(e, 0)), \ldots , f(u(e, n-1))\rangle .$
Verification. First, since f is dominated by h, and since the function
![]() $\langle -,\ldots , -\rangle $
computing an n-tuple is increasing on each variable, we can dominate g with the computable function
$\langle -,\ldots , -\rangle $
computing an n-tuple is increasing on each variable, we can dominate g with the computable function
Now, by contradiction, suppose g does not satisfy (2), i.e., suppose there exists
![]() $e, n$
such that
$e, n$
such that
![]() $|W_e^X|\leqslant n$
but
$|W_e^X|\leqslant n$
but
![]() $g(e, n)\in W_e^X$
. Because
$g(e, n)\in W_e^X$
. Because
![]() $W_e^X$
has fewer than n elements, we can suppose
$W_e^X$
has fewer than n elements, we can suppose
![]() $g(e, n)$
is the
$g(e, n)$
is the
![]() $i{\text {th}}$
one for a some
$i{\text {th}}$
one for a some
![]() $i<n$
. Thus the function
$i<n$
. Thus the function
![]() $\Phi _{u(e, i)}^X$
is constantly equal to
$\Phi _{u(e, i)}^X$
is constantly equal to
![]() $k_i$
where
$k_i$
where
![]() $g(e, n)=\langle k_0, \ldots , k_{n-1}\rangle $
, in particular
$g(e, n)=\langle k_0, \ldots , k_{n-1}\rangle $
, in particular
![]() $\Phi _{u(e, i)}^X(u(e, i))=k_i$
. But we also have
$\Phi _{u(e, i)}^X(u(e, i))=k_i$
. But we also have
implying
![]() $f(u(e, i))=k_i=\Phi _{u(e, i)}^X(u(e, i))$
, which is impossible as f is supposed to be
$f(u(e, i))=k_i=\Phi _{u(e, i)}^X(u(e, i))$
, which is impossible as f is supposed to be
![]() $\mathsf {DNC}_h(X)$
.
$\mathsf {DNC}_h(X)$
.
We are now ready to prove the following proposition. Conidis [Reference Conidis6] independently proved the same statement for
![]() $\mathsf {TAC}$
with a similar construction. Note that by the equivalence of
$\mathsf {TAC}$
with a similar construction. Note that by the equivalence of
![]() $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
with
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
with
![]() ${\mathsf {CAC\ for\ trees}}$
, Conidis result implies Proposition 3.11.
${\mathsf {CAC\ for\ trees}}$
, Conidis result implies Proposition 3.11.
Proposition 3.11. Let
![]() $S \subseteq \mathbb {N}^{<\mathbb {N}}$
be an instance of
$S \subseteq \mathbb {N}^{<\mathbb {N}}$
be an instance of
![]() $\mathsf {SAC}$
. Every set X of degree
$\mathsf {SAC}$
. Every set X of degree
![]() $\mathsf {DNC}_h(\emptyset ')$
, with h a computable function, computes a solution of S.
$\mathsf {DNC}_h(\emptyset ')$
, with h a computable function, computes a solution of S.
Remark 3.12. Once again, as in the case of Proposition 3.3, the proof here is carried purely as a computability statement, we have access to as much induction as we need.
Proof First, since X is of degree
![]() $\mathsf {DNC}_h$
for a computable function h, by Lemma 3.10, it computes a function
$\mathsf {DNC}_h$
for a computable function h, by Lemma 3.10, it computes a function
![]() $g:\mathbb {N}^2\to \mathbb {N}$
such that
$g:\mathbb {N}^2\to \mathbb {N}$
such that
![]() $\forall e, n, |W_e^{\emptyset '}|\leqslant n\implies g(e, n)\notin W_e^{\emptyset '}$
and which is dominated by a computable function
$\forall e, n, |W_e^{\emptyset '}|\leqslant n\implies g(e, n)\notin W_e^{\emptyset '}$
and which is dominated by a computable function
![]() $b:\mathbb {N}^2\to \mathbb {N}$
.
$b:\mathbb {N}^2\to \mathbb {N}$
.
The idea of this proof is the same as in Proposition 3.3, but this time we are going to use g to avoid selecting the potential “bad” element in each finite antichain, i.e., the element which is incompatible with only finitely many strings. For any finite set
![]() $A\subseteq S$
, let
$A\subseteq S$
, let
![]() $\psi _A : \mathbb {N} \to S$
be a bijection such that
$\psi _A : \mathbb {N} \to S$
be a bijection such that
![]() .
.
The procedure is the following. Initially,
![]() $S_0\mathrel {\mathop :}= S$
. At step k, assume
$S_0\mathrel {\mathop :}= S$
. At step k, assume
![]() $S_k \subseteq S$
has been defined. To find the desired antichain
$S_k \subseteq S$
has been defined. To find the desired antichain
![]() $A_k$
we use the fixed point theorem to find an index
$A_k$
we use the fixed point theorem to find an index
![]() $e_k$
such that
$e_k$
such that
![]() $\Phi _{e_k}^{\emptyset '}(n)$
is the procedure that halts if it finds an antichain
$\Phi _{e_k}^{\emptyset '}(n)$
is the procedure that halts if it finds an antichain
![]() $A\subseteq S_k$
whose size is greater than
$A\subseteq S_k$
whose size is greater than
![]() $b(e_k, 1)$
and
$b(e_k, 1)$
and
![]() $\psi _A(n)\in A$
, and finds (using
$\psi _A(n)\in A$
, and finds (using
![]() $\emptyset '$
) an integer m such that
$\emptyset '$
) an integer m such that
![]() $\forall \ell>m, \psi _A(\ell )\succ \psi _A(n)$
.
$\forall \ell>m, \psi _A(\ell )\succ \psi _A(n)$
.
Define
![]() $A_k\mathrel {\mathop :}= A$
. By choice of A and
$A_k\mathrel {\mathop :}= A$
. By choice of A and
![]() $e_k$
,
$e_k$
,
 $$\begin{align*}W_{e_k}^{\emptyset'}=\begin{cases} \{\psi^{-1}_A(\rho)\},&\text{if } A_k \text{ has a bad element }\rho,\\ \varnothing,&\text{otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}W_{e_k}^{\emptyset'}=\begin{cases} \{\psi^{-1}_A(\rho)\},&\text{if } A_k \text{ has a bad element }\rho,\\ \varnothing,&\text{otherwise.} \end{cases}\end{align*}$$
Finally we can define
![]() $\sigma _k\mathrel {\mathop :}= \psi _A(g(e_k, 1))$
. Indeed since
$\sigma _k\mathrel {\mathop :}= \psi _A(g(e_k, 1))$
. Indeed since
![]() $|W_{e_k}^{\emptyset '}|\leqslant 1$
by construction,
$|W_{e_k}^{\emptyset '}|\leqslant 1$
by construction,
![]() $g(e_k, 1)\notin W_{e_k}^{\emptyset '}$
. Moreover
$g(e_k, 1)\notin W_{e_k}^{\emptyset '}$
. Moreover
![]() $\sigma _k\in A_k$
, because
$\sigma _k\in A_k$
, because
![]() $g(e_k, 1)<b(e_k, 1)<|A_k|$
. This implies that
$g(e_k, 1)<b(e_k, 1)<|A_k|$
. This implies that
![]() $\sigma _k$
is not a bad element of
$\sigma _k$
is not a bad element of
![]() $A_k$
, in other words the set
$A_k$
, in other words the set
![]() $S_{k+1}\mathrel {\mathop :}= \{\tau \in S_k\mid \tau \bot \sigma _k \mbox { and } |\tau |> |\sigma _k| \}$
is infinite.
$S_{k+1}\mathrel {\mathop :}= \{\tau \in S_k\mid \tau \bot \sigma _k \mbox { and } |\tau |> |\sigma _k| \}$
is infinite.
4
 $\mathsf {ADS}$
and
$\mathsf {ADS}$
and
 $\mathsf {EM}$
$\mathsf {EM}$
Ramsey’s theorem for pairs admits a famous decomposition into the Ascending Descending Sequence theorem (
![]() $\mathsf {ADS}$
) and the Erdős–Moser theorem (
$\mathsf {ADS}$
) and the Erdős–Moser theorem (
![]() $\mathsf {EM}$
) over
$\mathsf {EM}$
) over
![]() $\mathsf {RCA}_0$
. As mentioned in the introduction, both statements are strictly weaker than
$\mathsf {RCA}_0$
. As mentioned in the introduction, both statements are strictly weaker than
![]() $\mathsf {RT}^2_2$
. Actually, these statements are generally thought of as decomposing Ramsey’s theorem for pairs into its disjunctiveness part with
$\mathsf {RT}^2_2$
. Actually, these statements are generally thought of as decomposing Ramsey’s theorem for pairs into its disjunctiveness part with
![]() $\mathsf {ADS}$
, and its compactness part with
$\mathsf {ADS}$
, and its compactness part with
![]() $\mathsf {EM}$
. Indeed, the standard proof of
$\mathsf {EM}$
. Indeed, the standard proof of
![]() $\mathsf {ADS}$
is disjunctive, and does not involve any notion of compactness, while the proof of
$\mathsf {ADS}$
is disjunctive, and does not involve any notion of compactness, while the proof of
![]() $\mathsf {EM}$
is non-disjunctive and implies
$\mathsf {EM}$
is non-disjunctive and implies
![]() $\mathsf {RWKL}$
, which is the compactness part of
$\mathsf {RWKL}$
, which is the compactness part of
![]() $\mathsf {RT}^2_2$
.
$\mathsf {RT}^2_2$
.
![]() $\mathsf {ADS}$
and
$\mathsf {ADS}$
and
![]() $\mathsf {EM}$
are relatively disjoint, in that they are only known to have the hyperimmunity principle as common consequence, which is a particularly weak principle. In this section, however, we show that
$\mathsf {EM}$
are relatively disjoint, in that they are only known to have the hyperimmunity principle as common consequence, which is a particularly weak principle. In this section, however, we show that
![]() ${\mathsf {CAC\ for\ trees}}$
follows from both
${\mathsf {CAC\ for\ trees}}$
follows from both
![]() $\mathsf {ADS}$
and
$\mathsf {ADS}$
and
![]() $\mathsf {EM}$
over
$\mathsf {EM}$
over
![]() $\mathsf {RCA}_0$
. We shall see in Section 5 that
$\mathsf {RCA}_0$
. We shall see in Section 5 that
![]() ${\mathsf {CAC\ for\ trees}}$
implies the hyperimmunity principle.
${\mathsf {CAC\ for\ trees}}$
implies the hyperimmunity principle.
The following proposition was proved by Dorais (personal communication) for
![]() $\mathsf {SHER}$
and independently by Conidis [Reference Conidis6] for
$\mathsf {SHER}$
and independently by Conidis [Reference Conidis6] for
![]() $\mathsf {TAC}$
. We adapted the proof of Dorais to obtain the following proposition.
$\mathsf {TAC}$
. We adapted the proof of Dorais to obtain the following proposition.
Proposition 4.1.
![]() $\mathsf {RCA}_0\vdash \mathsf {ADS}\implies {\mathsf {CAC\ for\ trees}}$
and
$\mathsf {RCA}_0\vdash \mathsf {ADS}\implies {\mathsf {CAC\ for\ trees}}$
and
![]() ${\mathsf {CAC\ for\ trees}} \leqslant _c\mathsf {ADS.}$
${\mathsf {CAC\ for\ trees}} \leqslant _c\mathsf {ADS.}$
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite tree. Define the total order
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite tree. Define the total order
![]() $<_0$
over T by
$<_0$
over T by
![]() $\sigma <_0\tau \iff \sigma \prec \tau \lor (\sigma \bot \tau \land \sigma (d)<_{\mathbb {N}}\tau (d))$
where
$\sigma <_0\tau \iff \sigma \prec \tau \lor (\sigma \bot \tau \land \sigma (d)<_{\mathbb {N}}\tau (d))$
where
![]() $d\mathrel {\mathop :}= \min \{k\in \mathbb {N}\mid \sigma (k)\neq \tau (k)\}$
. By
$d\mathrel {\mathop :}= \min \{k\in \mathbb {N}\mid \sigma (k)\neq \tau (k)\}$
. By
![]() $\mathsf {ADS}$
, there is an infinite ascending or descending sequence
$\mathsf {ADS}$
, there is an infinite ascending or descending sequence
![]() $(\sigma _i)$
for
$(\sigma _i)$
for
![]() $(T, <_0)$
.
$(T, <_0)$
.
If it is descending, there are two possibilities. Either
![]() , which means we eventually have an infinite
, which means we eventually have an infinite
![]() $\prec $
-decreasing sequence of strings, which is impossible. Or
$\prec $
-decreasing sequence of strings, which is impossible. Or
![]() $\exists ^{\infty } i, \sigma _i\bot \sigma _{i+1}$
, in which case we designate by
$\exists ^{\infty } i, \sigma _i\bot \sigma _{i+1}$
, in which case we designate by
![]() $(h_k)$
the sequence
$(h_k)$
the sequence
![]() $(\sigma _{\ell _k+1})_{k\in \mathbb {N}}$
of all such
$(\sigma _{\ell _k+1})_{k\in \mathbb {N}}$
of all such
![]() $\sigma _{i+1}$
, and we show that it is an antichain of T.
$\sigma _{i+1}$
, and we show that it is an antichain of T.
To do so, it suffices to prove by induction on m that
![]() . When
. When
![]() $m=1$
, due to how
$m=1$
, due to how
![]() $(\sigma _i)$
is structured, we have
$(\sigma _i)$
is structured, we have
![]() $\forall k, h_k\succcurlyeq \sigma _{\ell _k}\bot h_{k+1}$
. We now consider
$\forall k, h_k\succcurlyeq \sigma _{\ell _k}\bot h_{k+1}$
. We now consider
![]() $h_k$
and
$h_k$
and
![]() $h_{k+(m+1)}$
. By induction hypothesis,
$h_{k+(m+1)}$
. By induction hypothesis,
![]() and
and
![]() . Moreover since
. Moreover since
![]() $h_k>_0 h_{k+m}>_0h_{k+(m+1)}$
, we know there are minima d and e such that
$h_k>_0 h_{k+m}>_0h_{k+(m+1)}$
, we know there are minima d and e such that
![]() $h_k(d)>h_{k+m}(d)$
and
$h_k(d)>h_{k+m}(d)$
and
![]() $h_{k+m}(e)>h_{k+(m+1)}(e)$
. Now
$h_{k+m}(e)>h_{k+(m+1)}(e)$
. Now
![]() $e\leqslant d$
implies
$e\leqslant d$
implies
![]() $h_{k+(m+1)}(e)<h_{k+m}(e)=h_k(e)$
, and
$h_{k+(m+1)}(e)<h_{k+m}(e)=h_k(e)$
, and
![]() $e> d$
implies
$e> d$
implies
![]() $h_{k+(m+1)}(d)=h_{k+m}(d)<h_k(d)$
; in any case
$h_{k+(m+1)}(d)=h_{k+m}(d)<h_k(d)$
; in any case
![]() .
.
Now if the sequence
![]() $(\sigma _i)$
is ascending, we again distinguish two possibilities. Either
$(\sigma _i)$
is ascending, we again distinguish two possibilities. Either
![]() , which means we eventually obtain an infinite path of the tree. Or
, which means we eventually obtain an infinite path of the tree. Or
![]() $\exists ^{\infty } i, \sigma _i\bot \sigma _{i+1}$
, in which case we work in the same fashion as in the descending case (designate by
$\exists ^{\infty } i, \sigma _i\bot \sigma _{i+1}$
, in which case we work in the same fashion as in the descending case (designate by
![]() $(h_k)$
the sequence
$(h_k)$
the sequence
![]() $(\sigma _{\ell _k})_{k\in \mathbb {N}}$
of all such
$(\sigma _{\ell _k})_{k\in \mathbb {N}}$
of all such
![]() $\sigma _i$
, and show by induction on m that
$\sigma _i$
, and show by induction on m that
![]() ).
).
Proposition 4.2.
![]() $\mathsf {RCA}_0\vdash \mathsf {EM}\implies {\mathsf {CAC\ for\ trees}}$
and
$\mathsf {RCA}_0\vdash \mathsf {EM}\implies {\mathsf {CAC\ for\ trees}}$
and
![]() ${\mathsf {CAC\ for\ trees}} \leqslant _c\mathsf {EM.}$
${\mathsf {CAC\ for\ trees}} \leqslant _c\mathsf {EM.}$
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite tree. We first define a computable bijection
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite tree. We first define a computable bijection
![]() $\psi :\mathbb {N}\to T$
. To do so, let
$\psi :\mathbb {N}\to T$
. To do so, let
![]() $\varphi :\mathbb {N}^{<\mathbb {N}}\to \mathbb {N}$
be the bijection
$\varphi :\mathbb {N}^{<\mathbb {N}}\to \mathbb {N}$
be the bijection
![]() $ x_0\cdot \ldots \cdot x_{n-1}\mapsto p_0^{x_0}\times \cdots \times p_{n-1}^{x_{n-1}}-1 $
where
$ x_0\cdot \ldots \cdot x_{n-1}\mapsto p_0^{x_0}\times \cdots \times p_{n-1}^{x_{n-1}}-1 $
where
![]() $p_k$
is the
$p_k$
is the
![]() $k{\text {th}}$
prime number. The elements of the sequence
$k{\text {th}}$
prime number. The elements of the sequence
![]() $(\varphi ^{-1}(n))_{n\in \mathbb {N}}$
that are in T form a subsequence denoted
$(\varphi ^{-1}(n))_{n\in \mathbb {N}}$
that are in T form a subsequence denoted
![]() $(s_n)_{n\in \mathbb {N}}$
, and the function
$(s_n)_{n\in \mathbb {N}}$
, and the function
![]() $\psi :\mathbb {N}\to T$
is defined by
$\psi :\mathbb {N}\to T$
is defined by
![]() $n\mapsto s_n$
.
$n\mapsto s_n$
.
Note that, by construction, the range of
![]() $\psi $
is infinite and computable. Moreover, if
$\psi $
is infinite and computable. Moreover, if
![]() $\sigma \prec \tau \in T$
, then
$\sigma \prec \tau \in T$
, then
![]() $\varphi (\sigma ) < \varphi (\tau )$
, hence,
$\varphi (\sigma ) < \varphi (\tau )$
, hence,
![]() $\psi ^{-1}(\sigma ) < \psi ^{-1}(\tau )$
. Also note that the range of
$\psi ^{-1}(\sigma ) < \psi ^{-1}(\tau )$
. Also note that the range of
![]() $\psi $
is not necessarily a tree.
$\psi $
is not necessarily a tree.
Let
![]() $f: [\mathbb {N}]^2 \to 2$
be the coloring defined by
$f: [\mathbb {N}]^2 \to 2$
be the coloring defined by
![]() $f(\{x, y\}) = 1$
iff
$f(\{x, y\}) = 1$
iff
![]() $x <_{\mathbb {N}} y$
and
$x <_{\mathbb {N}} y$
and
![]() $\psi (x)\prec \psi (y)$
coincide. By
$\psi (x)\prec \psi (y)$
coincide. By
![]() $\mathsf {EM}$
, there is an infinite transitive set
$\mathsf {EM}$
, there is an infinite transitive set
![]() $S\subseteq \mathbb {N}$
, i.e.,
$S\subseteq \mathbb {N}$
, i.e.,
![]() $\forall i<2, \forall x{<} y{<} z\in S, f(x, y)=f(y, z)=i\implies f(x, z)=i$
$\forall i<2, \forall x{<} y{<} z\in S, f(x, y)=f(y, z)=i\implies f(x, z)=i$
Note that if there are
![]() $x<y\in S$
such that
$x<y\in S$
such that
![]() $f(x, y)=0$
, then
$f(x, y)=0$
, then
![]() $\forall z>y\in S, f(x, z)=0$
. Indeed given
$\forall z>y\in S, f(x, z)=0$
. Indeed given
![]() $x<y<z\in S$
such that
$x<y<z\in S$
such that
![]() $f(x, y)=0$
, either
$f(x, y)=0$
, either
![]() $f(y, z)=0$
, and so by transitivity we have
$f(y, z)=0$
, and so by transitivity we have
![]() $f(x, z)=0$
; or
$f(x, z)=0$
; or
![]() $f(y, z)=1$
, but in that case
$f(y, z)=1$
, but in that case
![]() $f(x, z)\neq 1$
because it is impossible to simultaneously have
$f(x, z)\neq 1$
because it is impossible to simultaneously have
![]() $\psi (y)\prec \psi (z)$
,
$\psi (y)\prec \psi (z)$
,
![]() $\psi (x)\prec \psi (z)$
and
$\psi (x)\prec \psi (z)$
and
![]() $\psi (x)\bot \psi (y)$
.
$\psi (x)\bot \psi (y)$
.
Now two cases are possible. Either
![]() $\exists ^{\infty } j\in \mathbb {N}, f(s_j, s_{j+1})=0$
, so consider the infinite set A made of all such
$\exists ^{\infty } j\in \mathbb {N}, f(s_j, s_{j+1})=0$
, so consider the infinite set A made of all such
![]() $s_j$
. Thanks to the previous property, A is f-homogeneous for the color
$s_j$
. Thanks to the previous property, A is f-homogeneous for the color
![]() $0$
, and so
$0$
, and so
![]() $\psi (A)$
is an infinite antichain. Or
$\psi (A)$
is an infinite antichain. Or
![]() $\forall ^{\infty } j\in \mathbb {N}, f(s_j, s_{j+1})=1$
, so there is a large enough
$\forall ^{\infty } j\in \mathbb {N}, f(s_j, s_{j+1})=1$
, so there is a large enough
![]() $k\in \mathbb {N}$
such that
$k\in \mathbb {N}$
such that
![]() $\psi (s_k)\prec \psi (s_{k+1})\prec \ldots $
, i.e., we found an infinite path.
$\psi (s_k)\prec \psi (s_{k+1})\prec \ldots $
, i.e., we found an infinite path.
5
 $\mathsf {TAC}$
, lowness, and hyperimmunity
$\mathsf {TAC}$
, lowness, and hyperimmunity
Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3] and Conidis [Reference Conidis6] respectively studied the reverse mathematics of
![]() ${\mathsf {CAC\ for\ trees}}$
and
${\mathsf {CAC\ for\ trees}}$
and
![]() $\mathsf {TAC}$
. Since
$\mathsf {TAC}$
. Since
![]() ${\mathsf {CAC\ for\ trees}}$
is computably equivalent to
${\mathsf {CAC\ for\ trees}}$
is computably equivalent to
![]() $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
and this equivalence also holds in reverse mathematics, the analysis of
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
and this equivalence also holds in reverse mathematics, the analysis of
![]() ${\mathsf {CAC\ for\ trees}}$
and
${\mathsf {CAC\ for\ trees}}$
and
![]() $\mathsf {TAC}$
is very similar. For example, Binns et al. [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.4] proved that for any fixed low set L, there is a computable instance of
$\mathsf {TAC}$
is very similar. For example, Binns et al. [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.4] proved that for any fixed low set L, there is a computable instance of
![]() ${\mathsf {CAC\ for\ trees}}$
with no L-computable solution, while Conidis [Reference Conidis6] proved the existence of a computable instance of
${\mathsf {CAC\ for\ trees}}$
with no L-computable solution, while Conidis [Reference Conidis6] proved the existence of a computable instance of
![]() $\mathsf {TAC}$
whose solutions are all of hyperimmune degree. In this section, we prove a general statement regarding
$\mathsf {TAC}$
whose solutions are all of hyperimmune degree. In this section, we prove a general statement regarding
![]() $\mathsf {TAC}$
(Theorem 5.1) and show that it encompasses both results.
$\mathsf {TAC}$
(Theorem 5.1) and show that it encompasses both results.
Theorem 5.1. Let
![]() $(A_n)$
be an uniform sequence of infinite
$(A_n)$
be an uniform sequence of infinite
![]() $\Delta _2^0$
sets. There is a computable instance of
$\Delta _2^0$
sets. There is a computable instance of
![]() $\mathsf {TAC}$
such that no
$\mathsf {TAC}$
such that no
![]() $A_n$
is a solution.
$A_n$
is a solution.
Proof First, for any n, let
![]() $e_n$
be the index of
$e_n$
be the index of
![]() $A_n$
, i.e.,
$A_n$
, i.e.,
![]() $\Phi _{e_n}^{\emptyset '}=A_n$
. We also write
$\Phi _{e_n}^{\emptyset '}=A_n$
. We also write
![]() $A_n[s]\mathrel {\mathop :}= \Phi _{e_n}^{\emptyset '[s]}[s]$
.
$A_n[s]\mathrel {\mathop :}= \Phi _{e_n}^{\emptyset '[s]}[s]$
.
Idea. We are going to construct a tree
![]() $T\subseteq 2^{<\mathbb {N}}$
, such that for each
$T\subseteq 2^{<\mathbb {N}}$
, such that for each
![]() $n\in \mathbb {N}$
, there is
$n\in \mathbb {N}$
, there is
![]() $\sigma _n\in A_n$
verifying
$\sigma _n\in A_n$
verifying
![]() $\sigma _n\notin T$
or
$\sigma _n\notin T$
or
![]() $\sigma _n\in T\land \forall ^{\infty }\tau \in T, \sigma _n\prec \tau $
. These requirements are respectively denoted
$\sigma _n\in T\land \forall ^{\infty }\tau \in T, \sigma _n\prec \tau $
. These requirements are respectively denoted
![]() $\mathcal {R}_n$
and
$\mathcal {R}_n$
and
![]() $\mathcal {S}_n$
, and
$\mathcal {S}_n$
, and
![]() $A_n$
cannot be an infinite antichain of T if one of them is met.
$A_n$
cannot be an infinite antichain of T if one of them is met.
The sequence
![]() $(\sigma _n)$
is constructed via a movable marker procedure, with steps s and sub-steps
$(\sigma _n)$
is constructed via a movable marker procedure, with steps s and sub-steps
![]() $e<s$
. At each step s we are going to manipulate an approximation
$e<s$
. At each step s we are going to manipulate an approximation
![]() $\sigma _n^s$
of
$\sigma _n^s$
of
![]() $\sigma _n$
, and variables
$\sigma _n$
, and variables
![]() $\widehat {\sigma }_n^s$
that will help us keep track of which requirement is satisfied by
$\widehat {\sigma }_n^s$
that will help us keep track of which requirement is satisfied by
![]() $\sigma _n^s$
.
$\sigma _n^s$
.
Construction. At the beginning of each step s, let
![]() $T_s$
be the approximation of the tree T defined by
$T_s$
be the approximation of the tree T defined by
![]() $T_s\mathrel {\mathop :}= T_{s-1}\cup \{\tau _s\cdot 0, \tau _s\cdot 1\}$
, where
$T_s\mathrel {\mathop :}= T_{s-1}\cup \{\tau _s\cdot 0, \tau _s\cdot 1\}$
, where
![]() $\tau _s$
is the leftmost (for example) leaf of
$\tau _s$
is the leftmost (for example) leaf of
![]() $T_{s-1}$
such that
$T_{s-1}$
such that
![]() $\tau _s\succcurlyeq \widehat {\sigma }_{s-1}^s$
. For
$\tau _s\succcurlyeq \widehat {\sigma }_{s-1}^s$
. For
![]() $s=0$
, we let
$s=0$
, we let
![]() $T_0\mathrel {\mathop :}= \{\varepsilon \}$
.
$T_0\mathrel {\mathop :}= \{\varepsilon \}$
.
At step s, sub-step e, let
![]() $\sigma _e^s$
be the string whose code is the smallest in the uniformly computable set
$\sigma _e^s$
be the string whose code is the smallest in the uniformly computable set
![]() $\{\tau \in A_e[s]{\upharpoonright }_{s}\mid (\tau \in T_s \land \tau \succcurlyeq \widehat {\sigma }_{e-1}^s) \lor \tau \notin T_s\}$
with
$\{\tau \in A_e[s]{\upharpoonright }_{s}\mid (\tau \in T_s \land \tau \succcurlyeq \widehat {\sigma }_{e-1}^s) \lor \tau \notin T_s\}$
with
![]() $\widehat {\sigma }_{-1}^s \mathrel {\mathop :}= \varepsilon $
and
$\widehat {\sigma }_{-1}^s \mathrel {\mathop :}= \varepsilon $
and
![]() $\sigma _e^s$
is undefined when the set is empty.
$\sigma _e^s$
is undefined when the set is empty.
Besides, define
 $\widehat {\sigma }_e^s \mathrel {\mathop :}= \begin {cases} \sigma _e^s,& \text {if }\sigma _e^s\in T_s\text { (and therefore }\sigma _e^s\succcurlyeq \widehat {\sigma }_{e-1}^s),\\ \widehat {\sigma }_{e-1}^s,& \text {otherwise.} \end {cases}$
$\widehat {\sigma }_e^s \mathrel {\mathop :}= \begin {cases} \sigma _e^s,& \text {if }\sigma _e^s\in T_s\text { (and therefore }\sigma _e^s\succcurlyeq \widehat {\sigma }_{e-1}^s),\\ \widehat {\sigma }_{e-1}^s,& \text {otherwise.} \end {cases}$
Verification. By induction on e, we prove that
![]() $\sigma _e\mathrel {\mathop :}= \lim _s\sigma _e^s$
exists and is an element of
$\sigma _e\mathrel {\mathop :}= \lim _s\sigma _e^s$
exists and is an element of
![]() $A_e$
, also we prove
$A_e$
, also we prove
![]() $\widehat {\sigma }_e\mathrel {\mathop :}= \lim _s\widehat {\sigma }_e^s$
exists, and
$\widehat {\sigma }_e\mathrel {\mathop :}= \lim _s\widehat {\sigma }_e^s$
exists, and
![]() $\sigma _e$
satisfies
$\sigma _e$
satisfies
![]() $\mathcal {R}_e$
or
$\mathcal {R}_e$
or
![]() $\mathcal {S}_e$
.
$\mathcal {S}_e$
.
Suppose we reached a step r such that for all
![]() $e'<e$
the values of
$e'<e$
the values of
![]() $\sigma _{e'}^r$
and
$\sigma _{e'}^r$
and
![]() $\widehat {\sigma }_{e'}^r$
have stabilized. And thus, for any step
$\widehat {\sigma }_{e'}^r$
have stabilized. And thus, for any step
![]() $s>r$
, as
$s>r$
, as
![]() $\tau _s\succcurlyeq \widehat {\sigma }_{s-1}^s\succcurlyeq \widehat {\sigma }_{e-1}^s = \widehat {\sigma }_{e-1}$
, the tree will always be extended with nodes above
$\tau _s\succcurlyeq \widehat {\sigma }_{s-1}^s\succcurlyeq \widehat {\sigma }_{e-1}^s = \widehat {\sigma }_{e-1}$
, the tree will always be extended with nodes above
![]() $\widehat {\sigma }_{e-1}$
, implying only a finite part of the tree is not above
$\widehat {\sigma }_{e-1}$
, implying only a finite part of the tree is not above
![]() $\widehat {\sigma }_{e-1}$
.
$\widehat {\sigma }_{e-1}$
.
Now suppose k is the smallest code of a string
![]() $\tau $
such that
$\tau $
such that
![]() $(\tau \in T\land \tau \succcurlyeq \widehat {\sigma }_{e-1})\lor \tau \notin T$
. Such a string exists because
$(\tau \in T\land \tau \succcurlyeq \widehat {\sigma }_{e-1})\lor \tau \notin T$
. Such a string exists because
![]() $A_e$
is infinite, whereas the set of strings in T that are below
$A_e$
is infinite, whereas the set of strings in T that are below
![]() $\widehat {\sigma }_{e-1}$
is not. If
$\widehat {\sigma }_{e-1}$
is not. If
![]() $\tau \in T$
, then
$\tau \in T$
, then
![]() $\exists x, \forall y\geqslant x, \tau \in T_y$
, otherwise define
$\exists x, \forall y\geqslant x, \tau \in T_y$
, otherwise define
![]() $x\mathrel {\mathop :}= 0$
. Since
$x\mathrel {\mathop :}= 0$
. Since
![]() $A_e$
is
$A_e$
is
![]() $\Delta _2^0$
, there exists
$\Delta _2^0$
, there exists
![]() $s\geqslant \max \{k+1, r, x\}$
such that
$s\geqslant \max \{k+1, r, x\}$
such that
![]() $A_e[s]{\upharpoonright }_{k+1}$
has stabilized, i.e.,
$A_e[s]{\upharpoonright }_{k+1}$
has stabilized, i.e.,
![]() $\forall t>s, A_e[t]{\upharpoonright }_{k+1}=A_e[s]{\upharpoonright }_{k+1}$
. Thus
$\forall t>s, A_e[t]{\upharpoonright }_{k+1}=A_e[s]{\upharpoonright }_{k+1}$
. Thus
![]() $\sigma _e^s=\tau $
because
$\sigma _e^s=\tau $
because
![]() $\tau \in A_e{\upharpoonright }_{k+1}= A_e[s]{\upharpoonright }_{k+1}\subseteq A_e[s]{\upharpoonright }_s$
. This ensures that for any
$\tau \in A_e{\upharpoonright }_{k+1}= A_e[s]{\upharpoonright }_{k+1}\subseteq A_e[s]{\upharpoonright }_s$
. This ensures that for any
![]() $t>s$
,
$t>s$
,
![]() $\sigma _e^t=\tau $
, i.e.,
$\sigma _e^t=\tau $
, i.e.,
![]() $\sigma _e=\tau $
.
$\sigma _e=\tau $
.
Finally, we distinguish two cases. Either
![]() $\sigma _e\in T$
and so
$\sigma _e\in T$
and so
![]() $\exists t, \sigma _e^t\in T_t$
, thus
$\exists t, \sigma _e^t\in T_t$
, thus
![]() $\forall u>t, \widehat {\sigma }_e^u=\sigma _e^u$
. So
$\forall u>t, \widehat {\sigma }_e^u=\sigma _e^u$
. So
![]() $\mathcal {S}_e$
is satisfied, as cofinitely many nodes of T will be above
$\mathcal {S}_e$
is satisfied, as cofinitely many nodes of T will be above
![]() $\widehat {\sigma }_e=\sigma _e$
. Or
$\widehat {\sigma }_e=\sigma _e$
. Or
![]() $\sigma _e\notin T$
, in which case, either
$\sigma _e\notin T$
, in which case, either
![]() $\forall t, \sigma _e^t\notin T_t$
, implying
$\forall t, \sigma _e^t\notin T_t$
, implying
![]() $\forall t, \widehat {\sigma }_e^{\kern1pt t}\mathrel {\mathop :}= \widehat {\sigma }_{e-1}^{\kern1pt t}$
and thus
$\forall t, \widehat {\sigma }_e^{\kern1pt t}\mathrel {\mathop :}= \widehat {\sigma }_{e-1}^{\kern1pt t}$
and thus
![]() $\mathcal {R}_e$
is satisfied.
$\mathcal {R}_e$
is satisfied.
We now show how Theorem 5.1 relates to the result of Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.4], that is, the existence, for any fixed low set L, of a computable instance of
![]() ${\mathsf {CAC\ for\ trees}}$
with no L-computable solution.
${\mathsf {CAC\ for\ trees}}$
with no L-computable solution.
Lemma 5.2. For any low set P, the sequence of infinite P-computable sets is uniformly
![]() $\Delta _2^0$
.
$\Delta _2^0$
.
Proof Since
![]() $P'\leqslant _T\emptyset '$
we can
$P'\leqslant _T\emptyset '$
we can
![]() $\emptyset '$
-compute the function
$\emptyset '$
-compute the function
 $$\begin{align*}f(e, x)=\begin{cases} \Phi_e^P(x), &\text{ when }\forall y\leqslant x, \Phi_e^P(y)\downarrow\text{ and }\exists y>x, \Phi_e^P(y)\downarrow=1,\\ 1, &\text{ otherwise.} \end{cases}\end{align*}$$
$$\begin{align*}f(e, x)=\begin{cases} \Phi_e^P(x), &\text{ when }\forall y\leqslant x, \Phi_e^P(y)\downarrow\text{ and }\exists y>x, \Phi_e^P(y)\downarrow=1,\\ 1, &\text{ otherwise.} \end{cases}\end{align*}$$
Now let
![]() $A_e\mathrel {\mathop :}= \{f(e, x)\mid x\in \mathbb {N}\}$
. If
$A_e\mathrel {\mathop :}= \{f(e, x)\mid x\in \mathbb {N}\}$
. If
![]() $\Phi _e^P$
is total and infinite then
$\Phi _e^P$
is total and infinite then
![]() $A_e$
is equal to it, so it is P-computable. Otherwise
$A_e$
is equal to it, so it is P-computable. Otherwise
![]() $A_e$
is cofinite, and in particular it is infinite and P-computable.
$A_e$
is cofinite, and in particular it is infinite and P-computable.
We are now ready to state the result of Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.4], but for
![]() $\mathsf {TAC}$
.
$\mathsf {TAC}$
.
Corollary 5.3. For any low set P, there exists a computable instance of
![]() $\kern1pt\mathsf {TAC}$
with no P-computable solution.
$\kern1pt\mathsf {TAC}$
with no P-computable solution.
The previous corollary is very useful to show that
![]() $\mathsf {RCA}_0 + \mathsf {WKL} \nvdash \mathsf {TAC}$
, since there exists a model of
$\mathsf {RCA}_0 + \mathsf {WKL} \nvdash \mathsf {TAC}$
, since there exists a model of
![]() $\mathsf {RCA}_0 + \mathsf {WKL}$
below a low set. The following corollary will be useful to prove that the result of Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.4] implies the result of Conidis.
$\mathsf {RCA}_0 + \mathsf {WKL}$
below a low set. The following corollary will be useful to prove that the result of Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Theorem 6.4] implies the result of Conidis.
Corollary 5.4. There exist a
![]() $\mathsf {PA}$
degree P and an instance of
$\mathsf {PA}$
degree P and an instance of
![]() $\mathsf {TAC}$
with no P-computable solution.
$\mathsf {TAC}$
with no P-computable solution.
Proof It follows from the existence of a low
![]() $\mathsf {PA}$
degree by the low basis theorem (see [Reference Jockusch and Soare15, Corollary 2.2.]).
$\mathsf {PA}$
degree by the low basis theorem (see [Reference Jockusch and Soare15, Corollary 2.2.]).
The next proposition has two purposes. First, it will be used to show the existence of a computable instance of
![]() $\mathsf {TAC}$
whose solutions are all of hyperimmune degree (see Theorem 5.6). Second, it shows that, for any such instance, one can choose two specific functionals to witness this hyperimmunity, without loss of generality (see Corollary 5.8).
$\mathsf {TAC}$
whose solutions are all of hyperimmune degree (see Theorem 5.6). Second, it shows that, for any such instance, one can choose two specific functionals to witness this hyperimmunity, without loss of generality (see Corollary 5.8).
Proposition 5.5. Let T be an instance of
![]() $\mathsf {TAC}$
. For any set P of
$\mathsf {TAC}$
. For any set P of
![]() $\mathsf {PA}$
degree, if T has no P-computable solution, then for any solution
$\mathsf {PA}$
degree, if T has no P-computable solution, then for any solution
![]() $(\sigma _n)_{n \in \mathbb {N}}$
, the function
$(\sigma _n)_{n \in \mathbb {N}}$
, the function
![]() $t_{T,(\sigma _n)_{n \in \mathbb {N}}} : n\mapsto \min \{t\mid \sigma _n\in T[t]\}$
or
$t_{T,(\sigma _n)_{n \in \mathbb {N}}} : n\mapsto \min \{t\mid \sigma _n\in T[t]\}$
or
![]() $\ell _{(\sigma _n)_{n \in \mathbb {N}}}:n\mapsto |\sigma _n|$
is hyperimmune.
$\ell _{(\sigma _n)_{n \in \mathbb {N}}}:n\mapsto |\sigma _n|$
is hyperimmune.
Proof By contraposition, suppose there exists a solution
![]() $(\sigma _n)_{n \in \mathbb {N}}$
such that
$(\sigma _n)_{n \in \mathbb {N}}$
such that
![]() $t_{T, (\sigma _n)_{n \in \mathbb {N}}}$
and
$t_{T, (\sigma _n)_{n \in \mathbb {N}}}$
and
![]() $\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
are computably dominated by t and
$\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
are computably dominated by t and
![]() $\ell $
respectively. Then the set
$\ell $
respectively. Then the set
 $$\begin{align*}\left\{(\tau_n)_{n \in \mathbb{N}} \;\middle| \begin{array}{l} (\tau_n)_{n \in \mathbb{N}}\text{ is an infinite antichain of }T\\ t_{T, (\tau_n)_{n \in \mathbb{N}}}\leqslant t\text{ and }\ell_{(\tau_n)_{n \in \mathbb{N}}}\leqslant\ell \end{array}\right\} \end{align*}$$
$$\begin{align*}\left\{(\tau_n)_{n \in \mathbb{N}} \;\middle| \begin{array}{l} (\tau_n)_{n \in \mathbb{N}}\text{ is an infinite antichain of }T\\ t_{T, (\tau_n)_{n \in \mathbb{N}}}\leqslant t\text{ and }\ell_{(\tau_n)_{n \in \mathbb{N}}}\leqslant\ell \end{array}\right\} \end{align*}$$
is a non-empty
![]() $\Pi _1^0$
class. It is non-empty because
$\Pi _1^0$
class. It is non-empty because
![]() $(\sigma _n)_{n \in \mathbb {N}}$
belongs to it, and to show it is a
$(\sigma _n)_{n \in \mathbb {N}}$
belongs to it, and to show it is a
![]() $\Pi _1^0$
class, it can be written as
$\Pi _1^0$
class, it can be written as
 $$\begin{align*}\left\{(\tau_n)_{n \in \mathbb{N}}\;\middle|\ \forall n, \begin{array}{l} \forall m<n, \tau_n\bot\tau_m\\ \tau_n\in T[t(n)]\\ |\tau_n|\leqslant\ell(n) \end{array}\right\}.\end{align*}$$
$$\begin{align*}\left\{(\tau_n)_{n \in \mathbb{N}}\;\middle|\ \forall n, \begin{array}{l} \forall m<n, \tau_n\bot\tau_m\\ \tau_n\in T[t(n)]\\ |\tau_n|\leqslant\ell(n) \end{array}\right\}.\end{align*}$$
Thanks to
![]() $\ell $
, the number of elements at each level n of the tree associated with this class is computably bounded by
$\ell $
, the number of elements at each level n of the tree associated with this class is computably bounded by
![]() $2^{\ell (n)}$
, thus it can be coded by a
$2^{\ell (n)}$
, thus it can be coded by a
![]() $\Pi _1^0$
class of
$\Pi _1^0$
class of
![]() $2^{\mathbb {N}}$
. Finally since P is of
$2^{\mathbb {N}}$
. Finally since P is of
![]() $\mathsf {PA}$
degree, it computes an element of any
$\mathsf {PA}$
degree, it computes an element of any
![]() $\Pi _1^0$
class of the Cantor space, hence the result.
$\Pi _1^0$
class of the Cantor space, hence the result.
Combining Corollary 5.4 and Proposition 5.5, we obtain the following theorem from Conidis [Reference Conidis6].
Theorem 5.6 [Reference Conidis6]
There is a computable instance of
![]() $\mathsf {TAC}$
such that each solution is of hyperimmune degree.
$\mathsf {TAC}$
such that each solution is of hyperimmune degree.
Proof Let P be of low PA degree. By using Corollary 5.3 we get a computable instance T of
![]() $\mathsf {TAC}$
with no P-computable solution. Thus, by using Proposition 5.5 we deduce that, for any solution
$\mathsf {TAC}$
with no P-computable solution. Thus, by using Proposition 5.5 we deduce that, for any solution
![]() $(\sigma _n)$
, its function
$(\sigma _n)$
, its function
![]() $t_{T, (\sigma _n)_{n \in \mathbb {N}}}$
or
$t_{T, (\sigma _n)_{n \in \mathbb {N}}}$
or
![]() $\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
is hyperimmune. And
$\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
is hyperimmune. And
![]() $(\sigma _n)_{n \in \mathbb {N}}$
computes both, since T is computable; meaning it is of hyperimmune degree.
$(\sigma _n)_{n \in \mathbb {N}}$
computes both, since T is computable; meaning it is of hyperimmune degree.
Corollary 5.7.
![]() $\mathsf {RCA}_0\vdash \mathsf {TAC}\implies \mathsf {HYP}$
.
$\mathsf {RCA}_0\vdash \mathsf {TAC}\implies \mathsf {HYP}$
.
In his direct proof of Theorem 5.6, Conidis [Reference Conidis6] constructed computable instance of
![]() $\mathsf {TAC}$
and two functionals
$\mathsf {TAC}$
and two functionals
![]() $\Phi , \Psi $
such that for every solution H, either
$\Phi , \Psi $
such that for every solution H, either
![]() $\Phi ^H$
or
$\Phi ^H$
or
![]() $\Psi ^H$
is hyperimmune. Interestingly, Proportion 5.5 can be used to show that
$\Psi ^H$
is hyperimmune. Interestingly, Proportion 5.5 can be used to show that
![]() $\Phi $
and
$\Phi $
and
![]() $\Psi $
can be chosen to be
$\Psi $
can be chosen to be
![]() $t_{T, -}$
and
$t_{T, -}$
and
![]() $\ell _-$
, without loss of generality.
$\ell _-$
, without loss of generality.
Corollary 5.8. For any instance T of
![]() $\kern1pt\mathsf {TAC}$
whose solutions are all of hyperimmune degree, at least one of the function
$\kern1pt\mathsf {TAC}$
whose solutions are all of hyperimmune degree, at least one of the function
![]() $t_{T, -}$
or
$t_{T, -}$
or
![]() $\ell _-$
is a witness.
$\ell _-$
is a witness.
Proof Let T be an instance of
![]() $\mathsf {TAC}$
whose solutions are all of hyperimmune degree, and let
$\mathsf {TAC}$
whose solutions are all of hyperimmune degree, and let
![]() $(\sigma _n)_{n \in \mathbb {N}}$
be such a solution. By contradiction, if we suppose
$(\sigma _n)_{n \in \mathbb {N}}$
be such a solution. By contradiction, if we suppose
![]() $t_{T, (\sigma _n)_{n \in \mathbb {N}}}$
and
$t_{T, (\sigma _n)_{n \in \mathbb {N}}}$
and
![]() $\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
are both computably dominated, then by Proposition 5.5, T has a P-computable solution. If we choose P to be computably dominated, then it cannot compute a solution of hyperimmune degree, hence a contradiction.
$\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
are both computably dominated, then by Proposition 5.5, T has a P-computable solution. If we choose P to be computably dominated, then it cannot compute a solution of hyperimmune degree, hence a contradiction.
Note that for every (computable or not) instance of
![]() $\mathsf {TAC}$
, there is a solution
$\mathsf {TAC}$
, there is a solution
![]() $(\sigma _n)_{n \in \mathbb {N}}$
such that
$(\sigma _n)_{n \in \mathbb {N}}$
such that
![]() $\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
is dominated by the identity function, by picking any path, and building an antichain along it.
$\ell _{(\sigma _n)_{n \in \mathbb {N}}}$
is dominated by the identity function, by picking any path, and building an antichain along it.
6
 $\mathsf {SHER}$
$\mathsf {SHER}$
We have seen in Section 4 that
![]() ${\mathsf {CAC\ for\ trees}}$
follows from both
${\mathsf {CAC\ for\ trees}}$
follows from both
![]() $\mathsf {ADS}$
and
$\mathsf {ADS}$
and
![]() $\mathsf {EM}$
over
$\mathsf {EM}$
over
![]() $\mathsf {RCA}_0$
. The proof of
$\mathsf {RCA}_0$
. The proof of
![]() ${\mathsf {CAC\ for\ trees}}$
from
${\mathsf {CAC\ for\ trees}}$
from
![]() $\mathsf {ADS}$
used only one specific property of the partial order
$\mathsf {ADS}$
used only one specific property of the partial order
![]() $(T, \prec )$
, that we shall refer to as semi-heredity. Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8] introduced the principle
$(T, \prec )$
, that we shall refer to as semi-heredity. Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8] introduced the principle
![]() $\mathsf {SHER}$
, which is the restriction of Ramsey’s theorem for pairs to semi-hereditary colorings. In this section, we show that the seemingly artificial principle
$\mathsf {SHER}$
, which is the restriction of Ramsey’s theorem for pairs to semi-hereditary colorings. In this section, we show that the seemingly artificial principle
![]() $\mathsf {SHER}$
turns out to be equivalent to the rather natural principle
$\mathsf {SHER}$
turns out to be equivalent to the rather natural principle
![]() ${\mathsf {CAC\ for\ trees}}$
. This equivalence can be seen as more step towards the robustness of
${\mathsf {CAC\ for\ trees}}$
. This equivalence can be seen as more step towards the robustness of
![]() ${\mathsf {CAC\ for\ trees}}$
.
${\mathsf {CAC\ for\ trees}}$
.
Definition 6.1 (Semi-heredity)
A coloring
![]() $f:[\mathbb {N}]^2\to 2$
is semi-here ditary for the color
$f:[\mathbb {N}]^2\to 2$
is semi-here ditary for the color
![]() $i<2$
if
$i<2$
if
The name “semi-heredity” comes from the contraposition of the previous definition
![]() $\forall x{<} y{<} z, f(x, y)=1-i\implies f(x, z)=1-i\lor f(y, z)=1-i.$
$\forall x{<} y{<} z, f(x, y)=1-i\implies f(x, z)=1-i\lor f(y, z)=1-i.$
Definition 6.2 (
 $\mathsf {SHER}$
, [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8])
$\mathsf {SHER}$
, [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8])
For any semi-hereditary coloring f, there exists an infinite f-homogeneous set.
The first proposition consists essentially of noticing that, given a set of strings
![]() $T \subseteq \mathbb {N}^{<\mathbb {N}}$
, the partial order
$T \subseteq \mathbb {N}^{<\mathbb {N}}$
, the partial order
![]() $(T, \prec )$
behaves like a semi-hereditary coloring. The whole technicality of the proposition comes from the definition of an injection
$(T, \prec )$
behaves like a semi-hereditary coloring. The whole technicality of the proposition comes from the definition of an injection
![]() $\psi : \mathbb {N} \to T$
with some desired properties.
$\psi : \mathbb {N} \to T$
with some desired properties.
Proposition 6.3.
![]() $\mathsf {RCA}_0\vdash \mathsf {SHER}\implies {\mathsf {CAC\ for\ c.e.\ trees}}$
and
$\mathsf {RCA}_0\vdash \mathsf {SHER}\implies {\mathsf {CAC\ for\ c.e.\ trees}}$
and
![]() ${\mathsf {CAC\ for\ c.e.\ trees}}\leqslant _c\mathsf {SHER.}$
${\mathsf {CAC\ for\ c.e.\ trees}}\leqslant _c\mathsf {SHER.}$
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite c.e. tree. First, let
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite c.e. tree. First, let
![]() $\varphi :\mathbb {N}^{<\mathbb {N}}\to \mathbb {N}$
the bijection
$\varphi :\mathbb {N}^{<\mathbb {N}}\to \mathbb {N}$
the bijection
![]() $ x_0\cdot \ldots \cdot x_{n-1}\mapsto p_0^{x_0}\times \cdots \times p_{n-1}^{x_{n-1}}-1 $
where
$ x_0\cdot \ldots \cdot x_{n-1}\mapsto p_0^{x_0}\times \cdots \times p_{n-1}^{x_{n-1}}-1 $
where
![]() $p_k$
is the
$p_k$
is the
![]() $k{\text {th}}$
prime number. Define
$k{\text {th}}$
prime number. Define
![]() $\psi : \mathbb {N} \to T$
by letting
$\psi : \mathbb {N} \to T$
by letting
![]() $\psi (n)$
be the least
$\psi (n)$
be the least
![]() $\sigma \in T$
(in order of apparition) such that
$\sigma \in T$
(in order of apparition) such that
![]() $\phi (\sigma )$
is bigger than
$\phi (\sigma )$
is bigger than
![]() $\phi (\psi (0)), \phi (\psi (1)), \dots , \phi (\psi (n-1))$
. Note that, by construction, the range of
$\phi (\psi (0)), \phi (\psi (1)), \dots , \phi (\psi (n-1))$
. Note that, by construction, the range of
![]() $\psi $
is infinite and computable. Moreover, if
$\psi $
is infinite and computable. Moreover, if
![]() $\sigma \prec \tau $
, then
$\sigma \prec \tau $
, then
![]() $\varphi (\sigma ) < \varphi (\tau )$
, hence
$\varphi (\sigma ) < \varphi (\tau )$
, hence
![]() $\psi ^{-1}(\sigma ) < \psi ^{-1}(\tau )$
. Also note that the range of
$\psi ^{-1}(\sigma ) < \psi ^{-1}(\tau )$
. Also note that the range of
![]() $\psi $
is not necessarily a tree.
$\psi $
is not necessarily a tree.
Let
![]() $f: [\mathbb {N}]^2 \to 2$
be the coloring defined by
$f: [\mathbb {N}]^2 \to 2$
be the coloring defined by
![]() $f(\{x, y\}) = 1$
iff
$f(\{x, y\}) = 1$
iff
![]() $x <_{\mathbb {N}} y$
and
$x <_{\mathbb {N}} y$
and
![]() $\psi (x)\prec \psi (y)$
coincide. Let us show that f is semi-hereditary for the color 1. Suppose we have
$\psi (x)\prec \psi (y)$
coincide. Let us show that f is semi-hereditary for the color 1. Suppose we have
![]() $x<y<z$
and that
$x<y<z$
and that
![]() $f(x, z)=f(y, z)=1$
, i.e., letting
$f(x, z)=f(y, z)=1$
, i.e., letting
![]() $\sigma \mathrel {\mathop :}= \psi (x), \tau \mathrel {\mathop :}= \psi (y), \rho \mathrel {\mathop :}= \psi (z)$
then we have
$\sigma \mathrel {\mathop :}= \psi (x), \tau \mathrel {\mathop :}= \psi (y), \rho \mathrel {\mathop :}= \psi (z)$
then we have
![]() $\sigma \prec \rho $
and
$\sigma \prec \rho $
and
![]() $\tau \prec \rho $
, thus either
$\tau \prec \rho $
, thus either
![]() $\sigma \prec \tau $
or
$\sigma \prec \tau $
or
![]() $\tau \prec \sigma $
. But since
$\tau \prec \sigma $
. But since
![]() $x<y$
, i.e.,
$x<y$
, i.e.,
![]() $\psi ^{-1}(\sigma )<\psi ^{-1}(\tau )$
, only
$\psi ^{-1}(\sigma )<\psi ^{-1}(\tau )$
, only
![]() $\sigma \prec \tau $
can hold due to the above note, meaning
$\sigma \prec \tau $
can hold due to the above note, meaning
![]() $f(x, y)=1$
.
$f(x, y)=1$
.
By
![]() $\mathsf {SHER}$
applied to f, there is an infinite f-homogeneous set H. If it is homogeneous for the color 0, then the set
$\mathsf {SHER}$
applied to f, there is an infinite f-homogeneous set H. If it is homogeneous for the color 0, then the set
![]() $\psi (H)$
corresponds to an infinite antichain of T. Likewise, if it is homogeneous for the color 1, then the set
$\psi (H)$
corresponds to an infinite antichain of T. Likewise, if it is homogeneous for the color 1, then the set
![]() $\psi (H)$
is an infinite path of T.
$\psi (H)$
is an infinite path of T.
We now prove the converse of the previous proposition.
Definition 6.4 (Weak homogeneity)
Given a coloring
![]() $f:[\mathbb {N}]^2\to k$
, a set
$f:[\mathbb {N}]^2\to k$
, a set
![]() $A\mathrel {\mathop :}= \{a_0 < a_1 < \ldots \}\subseteq \mathbb {N}$
is weakly-homogeneous for the color
$A\mathrel {\mathop :}= \{a_0 < a_1 < \ldots \}\subseteq \mathbb {N}$
is weakly-homogeneous for the color
![]() $i<k$
if
$i<k$
if
![]() $\forall j, f(a_j, a_{j+1})=i.$
$\forall j, f(a_j, a_{j+1})=i.$
Before proving Proposition 6.6, we need a technical lemma.
Lemma 6.5 (
 $\mathsf {RCA}_0$
)
$\mathsf {RCA}_0$
)
Let
![]() $f:[\mathbb {N}]^2\to 2$
be a semi-hereditary coloring for the color
$f:[\mathbb {N}]^2\to 2$
be a semi-hereditary coloring for the color
![]() $i<2$
. For every infinite set
$i<2$
. For every infinite set
![]() $A\mathrel {\mathop :}= \{a_0 < a_1 <\ldots \}$
which is weakly-homogeneous for the color i, there is an infinite f-homogeneous subset
$A\mathrel {\mathop :}= \{a_0 < a_1 <\ldots \}$
which is weakly-homogeneous for the color i, there is an infinite f-homogeneous subset
![]() $B \subseteq A$
.
$B \subseteq A$
.
Proof (Dorais)
We first show that any
![]() $a_j$
falls in one of these two categories:
$a_j$
falls in one of these two categories:
-
1.
 $\forall k>j, f(a_j, a_k)=i.$
$\forall k>j, f(a_j, a_k)=i.$
-
2.

Indeed, for any
![]() $\ell>j$
such that
$\ell>j$
such that
![]() $f(a_j, a_{\ell })=i$
, by semi-heredity,
$f(a_j, a_{\ell })=i$
, by semi-heredity,
![]() $f(a_j, a_{\ell -1})=i$
. So with a finite induction we get
$f(a_j, a_{\ell -1})=i$
. So with a finite induction we get
![]() .
.
There are now two possibilities. Either there are finitely many
![]() $a_j$
of type 2, and so by removing these elements, the resulting set is f-homogeneous for the color i. Otherwise there are infinitely many
$a_j$
of type 2, and so by removing these elements, the resulting set is f-homogeneous for the color i. Otherwise there are infinitely many
![]() $a_j$
of type 2, in which case one can define an infinite f-homogeneous subset for color
$a_j$
of type 2, in which case one can define an infinite f-homogeneous subset for color
![]() $1-i$
using
$1-i$
using
![]() $\mathsf {B}\Sigma _1^0(A)$
as follows: due to the observation above, “
$\mathsf {B}\Sigma _1^0(A)$
as follows: due to the observation above, “
![]() $a_j$
is of type 2” is equivalent to the
$a_j$
is of type 2” is equivalent to the
![]() $\Sigma ^0_1(A)$
formula
$\Sigma ^0_1(A)$
formula
![]() $\exists \ell>j, f(a_j, a_{\ell })=1-i$
. Thus, given a finite set of type 2 elements
$\exists \ell>j, f(a_j, a_{\ell })=1-i$
. Thus, given a finite set of type 2 elements
![]() $\{a_{j_0}, \ldots , a_{j_{k-1}}\}$
, by
$\{a_{j_0}, \ldots , a_{j_{k-1}}\}$
, by
![]() $\mathsf {B}\Sigma _1^0(A)$
there is
$\mathsf {B}\Sigma _1^0(A)$
there is
![]() $b>\max \{j_0, \ldots , j_{k-1}\}$
, and so
$b>\max \{j_0, \ldots , j_{k-1}\}$
, and so
![]() $j_k$
is defined as the smallest integer
$j_k$
is defined as the smallest integer
![]() $j_k$
such that
$j_k$
such that
![]() $j_k\geqslant b$
and
$j_k\geqslant b$
and
![]() $f(a_{j_{k-1}}, a_{j_k})=1-i$
.
$f(a_{j_{k-1}}, a_{j_k})=1-i$
.
Proposition 6.6.
![]() $\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ trees}} \implies \mathsf {SHER}$
and
$\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ trees}} \implies \mathsf {SHER}$
and
![]() $\mathsf {SHER}\leqslant _c{\mathsf {CAC\ for\ trees}}.$
$\mathsf {SHER}\leqslant _c{\mathsf {CAC\ for\ trees}}.$
Proof Let
![]() $f:[\mathbb {N}]^2\to 2$
be a semi-hereditary coloring for the color
$f:[\mathbb {N}]^2\to 2$
be a semi-hereditary coloring for the color
![]() $i<2$
. We begin by constructing a tree
$i<2$
. We begin by constructing a tree
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
defined as
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
defined as
![]() $T\mathrel {\mathop :}= \{\sigma _n\mid n\in \mathbb {N}\}$
, where
$T\mathrel {\mathop :}= \{\sigma _n\mid n\in \mathbb {N}\}$
, where
![]() $\sigma _n$
is the unique string which is:
$\sigma _n$
is the unique string which is:
-
1. strictly increasing (as a function), with last element
 $n;$
$n;$
-
2. weak-homogeneous for the color i, i.e.,
 $\forall k<|\sigma _n|-1, f(\sigma _n(k), \sigma _n(k+1))=i;$
$\forall k<|\sigma _n|-1, f(\sigma _n(k), \sigma _n(k+1))=i;$
-
3. maximal as a weak-homogeneous set, i.e.,
 $\forall y < \sigma _n(0), f(y, \sigma _n(0))=1-i$
and
$\forall y < \sigma _n(0), f(y, \sigma _n(0))=1-i$
and

To ensure existence, unicity and that T is a tree, we prove
![]() $\sigma _n$
is obtained via the following effective procedure. Start with the string n. If the string
$\sigma _n$
is obtained via the following effective procedure. Start with the string n. If the string
![]() $s_0\cdot \ldots \cdot s_m$
has been constructed, then look for the biggest integer
$s_0\cdot \ldots \cdot s_m$
has been constructed, then look for the biggest integer
![]() $j<s_0$
such that
$j<s_0$
such that
![]() $f\,(j, s_0)=i$
. If there is none, the process ends. Else, the process is repeated with the string
$f\,(j, s_0)=i$
. If there is none, the process ends. Else, the process is repeated with the string
![]() $j\cdot s_0\cdot \ldots \cdot s_m$
.
$j\cdot s_0\cdot \ldots \cdot s_m$
.
The string obtained is maximal by construction. It is unique, because at each step, if there are two (or more) integers
![]() $j_0<j_1$
smaller than
$j_0<j_1$
smaller than
![]() $s_0$
and such that
$s_0$
and such that
![]() $f\,(j_0, s_0)=f\,(j_1, s_0)=i$
, then by semi-heredity we have
$f\,(j_0, s_0)=f\,(j_1, s_0)=i$
, then by semi-heredity we have
![]() $f\,(j_0, j_1)=1$
. This means we will eventually add
$f\,(j_0, j_1)=1$
. This means we will eventually add
![]() $j_0$
after
$j_0$
after
![]() $j_1$
. In particular, the string contains all the
$j_1$
. In particular, the string contains all the
![]() $j<n$
such that
$j<n$
such that
![]() $f\,(j, n)=i$
. Moreover this shows that T is a tree, since the procedure is the same at any point during construction.
$f\,(j, n)=i$
. Moreover this shows that T is a tree, since the procedure is the same at any point during construction.
Now we can apply
![]() ${\mathsf {CAC\ for\ trees}}$
to T, leading to two possibilities. Either there is an infinite path, which is a weakly-homogeneous set for the color i thanks to condition 2. And so apply Lemma 6.5 to obtain a f-homogeneous set for the color i.
${\mathsf {CAC\ for\ trees}}$
to T, leading to two possibilities. Either there is an infinite path, which is a weakly-homogeneous set for the color i thanks to condition 2. And so apply Lemma 6.5 to obtain a f-homogeneous set for the color i.
Or there is an infinite antichain, which is of the form
![]() $(\sigma _{n_j})_{j\in \mathbb {N}}$
. Let us show the set
$(\sigma _{n_j})_{j\in \mathbb {N}}$
. Let us show the set
![]() $H\mathrel {\mathop :}= \{n_j\mid j\in \mathbb {N}\}$
is f-homogeneous for the color
$H\mathrel {\mathop :}= \{n_j\mid j\in \mathbb {N}\}$
is f-homogeneous for the color
![]() $1-i$
. Indeed, if
$1-i$
. Indeed, if
![]() $f(n_s, n_t) = i$
for some
$f(n_s, n_t) = i$
for some
![]() $s < t$
, then
$s < t$
, then
![]() $n_s \in \sigma _{n_t}$
, since
$n_s \in \sigma _{n_t}$
, since
![]() $\sigma _{n_t}$
contains all the elements
$\sigma _{n_t}$
contains all the elements
![]() $y < n_t$
such that
$y < n_t$
such that
![]() $f(y, n_t) = i$
. But then
$f(y, n_t) = i$
. But then
![]() $\sigma _{n_s} \prec \sigma _{n_t}$
, contradicting the fact that
$\sigma _{n_s} \prec \sigma _{n_t}$
, contradicting the fact that
![]() $(\sigma _{n_j})_{j\in \mathbb {N}}$
is an antichain.
$(\sigma _{n_j})_{j\in \mathbb {N}}$
is an antichain.
We end this section by studying
![]() $\mathsf {RT}_2^2$
with respect to 3-variables forbidden patterns. As explained in the introduction, there are three basic 3-variables forbidden patterns, yielding the notions of semi-heredity, semi-ancestry, and semi-transitivity, respectively. These forbidden patterns induce Ramsey-like statements of the form “for any 2-coloring of pairs, there exists an infinite set which avoids some kind of forbidden patterns.” This statement applied to semi-transitivity yields a consequence of the Erdős–Moser theorem, known to be strictly weaker than Ramsey’s theorem for pairs over
$\mathsf {RT}_2^2$
with respect to 3-variables forbidden patterns. As explained in the introduction, there are three basic 3-variables forbidden patterns, yielding the notions of semi-heredity, semi-ancestry, and semi-transitivity, respectively. These forbidden patterns induce Ramsey-like statements of the form “for any 2-coloring of pairs, there exists an infinite set which avoids some kind of forbidden patterns.” This statement applied to semi-transitivity yields a consequence of the Erdős–Moser theorem, known to be strictly weaker than Ramsey’s theorem for pairs over
![]() $\mathsf {RCA}_0$
. We now show that the two remaining forbidden patterns yield statements equivalent to
$\mathsf {RCA}_0$
. We now show that the two remaining forbidden patterns yield statements equivalent to
![]() $\mathsf {RT}_2^2$
. This completes the picture of the reverse mathematics of Ramsey-like theorems for 3-variable forbidden patterns.
$\mathsf {RT}_2^2$
. This completes the picture of the reverse mathematics of Ramsey-like theorems for 3-variable forbidden patterns.
Definition 6.7 (Semi-ancestry)
A coloring
![]() $f:[\mathbb {N}]^2\to 2$
has semi-ancestry for the color
$f:[\mathbb {N}]^2\to 2$
has semi-ancestry for the color
![]() $i<2$
if
$i<2$
if
Before proving
![]() $\mathsf {RT}^2_2$
from the Ramsey-like statement about semi-ancestry over
$\mathsf {RT}^2_2$
from the Ramsey-like statement about semi-ancestry over
![]() $\mathsf {RCA}_0$
, we need to prove that this statement implies
$\mathsf {RCA}_0$
, we need to prove that this statement implies
![]() $\mathsf {B}\Sigma ^0_2$
. This is done by proving the following principle.
$\mathsf {B}\Sigma ^0_2$
. This is done by proving the following principle.
Definition 6.8 (
 $\mathsf {D}_2^2$
)
$\mathsf {D}_2^2$
)
Every
![]() $\Delta _2^0$
set admits an infinite subset in it or its complement.
$\Delta _2^0$
set admits an infinite subset in it or its complement.
Proposition 6.9. The statement “for any 2-coloring of pairs, there exists an infinite set which has semi-ancestry for some color” implies
![]() $\mathsf {D}_2^2$
over
$\mathsf {D}_2^2$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proof Let A be a
![]() $\Delta _2^0$
set whose approximations are
$\Delta _2^0$
set whose approximations are
![]() $(A_t)_{t\in \mathbb {N}}$
. We define the coloring
$(A_t)_{t\in \mathbb {N}}$
. We define the coloring
![]() $f(x, y)\mathrel {\mathop :}= \chi _{A_y}(x)$
, and use the statement of the proposition to obtain an infinite set B that has semi-ancestry for some color.
$f(x, y)\mathrel {\mathop :}= \chi _{A_y}(x)$
, and use the statement of the proposition to obtain an infinite set B that has semi-ancestry for some color.
If B has semi-ancestry for the color 1, then
![]() $\forall x{<} y{<} z\in B, x\in A_y\land x\in A_z\implies y\in A_z$
. Now either
$\forall x{<} y{<} z\in B, x\in A_y\land x\in A_z\implies y\in A_z$
. Now either
![]() $B\subseteq \overline {A}$
and we are done. Or
$B\subseteq \overline {A}$
and we are done. Or
![]() $\exists x\in A\cap B$
, which means
$\exists x\in A\cap B$
, which means
![]() $\forall ^{\infty } y\in B, x\in A_y$
, implying that
$\forall ^{\infty } y\in B, x\in A_y$
, implying that
![]() $\forall ^{\infty } y>x\in B, \forall z>y\in B, y\in A_z$
by semi-ancestry, i.e.,
$\forall ^{\infty } y>x\in B, \forall z>y\in B, y\in A_z$
by semi-ancestry, i.e.,
![]() $\forall ^{\infty } y>x\in B, y\in A$
. So we can compute a subset H of B which is infinite and such that
$\forall ^{\infty } y>x\in B, y\in A$
. So we can compute a subset H of B which is infinite and such that
![]() $H\subseteq A$
.
$H\subseteq A$
.
This argument also works when B has semi-ancestry for the color 0, we just need to switch A and
![]() $\overline {A}$
, as well as
$\overline {A}$
, as well as
![]() $\in $
and
$\in $
and
![]() $\notin $
, when needed.
$\notin $
, when needed.
Corollary 6.10. The statement “for any 2-coloring of pairs, there exists an infinite set which has semi-ancestry for some color” implies
![]() $\mathsf {B}\Sigma ^0_2$
over
$\mathsf {B}\Sigma ^0_2$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proof Immediate, since
![]() $\mathsf {RCA}_0\vdash \mathsf {D}_2^2\implies \mathsf {B}\Sigma ^0_2$
(see [Reference Chong, Lempp and Yang5, Theorem 1.4]).
$\mathsf {RCA}_0\vdash \mathsf {D}_2^2\implies \mathsf {B}\Sigma ^0_2$
(see [Reference Chong, Lempp and Yang5, Theorem 1.4]).
Proposition 6.11. The statement “for any 2-coloring of pairs, there exists an infinite set which has semi-ancestry for some color” implies
![]() $\mathsf {RT}_2^2$
over
$\mathsf {RT}_2^2$
over
![]() $\mathsf {RCA}_0$
and over the computable reduction.
$\mathsf {RCA}_0$
and over the computable reduction.
Proof Let
![]() $f:[\mathbb {N}]^2\to 2$
be a coloring. We can apply the statement to obtain an infinite set A which has semi-ancestry for the color i, i.e.,
$f:[\mathbb {N}]^2\to 2$
be a coloring. We can apply the statement to obtain an infinite set A which has semi-ancestry for the color i, i.e.,
![]() $\forall x{<} y{<} z\in A, f(x, y)=i\land f(x, z)=i\implies f(y, z)=i$
. There are two possibilities. Either there exists
$\forall x{<} y{<} z\in A, f(x, y)=i\land f(x, z)=i\implies f(y, z)=i$
. There are two possibilities. Either there exists
![]() $a\in A$
such that
$a\in A$
such that
![]() $\exists ^{\infty } b>a\in A, f(a, b)=i$
, in which case all such elements b form an infinite f-homogeneous set due to the property of A. Otherwise any
$\exists ^{\infty } b>a\in A, f(a, b)=i$
, in which case all such elements b form an infinite f-homogeneous set due to the property of A. Otherwise any
![]() $a\in A$
verifies
$a\in A$
verifies
![]() $\forall ^{\infty } b>a, f(a, b)=1-i$
, i.e., all the elements of A have a limit color equal to
$\forall ^{\infty } b>a, f(a, b)=1-i$
, i.e., all the elements of A have a limit color equal to
![]() $1-i$
for the coloring
$1-i$
for the coloring
![]() $f{\upharpoonright }_{[A]^2}$
. Thus we can use
$f{\upharpoonright }_{[A]^2}$
. Thus we can use
![]() $\mathsf {B}\Sigma ^0_2$
(Corollary 6.10) to compute an infinite homogeneous set (see [Reference Dzhafarov, Hirschfeldt and Reitzes9, Proposition 6.2]).
$\mathsf {B}\Sigma ^0_2$
(Corollary 6.10) to compute an infinite homogeneous set (see [Reference Dzhafarov, Hirschfeldt and Reitzes9, Proposition 6.2]).
The proof that the Ramsey-like statement about semi-heredity implies Ramsey’s theorem for pairs is indirect, and uses the Ascending Descending Sequence principle.
Proposition 6.12. The statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color” implies
![]() $\mathsf {ADS}$
over
$\mathsf {ADS}$
over
![]() $\mathsf {RCA}_0$
and over the computable reduction.
$\mathsf {RCA}_0$
and over the computable reduction.
Proof Let
![]() $\mathcal {L} = (\mathbb {N}, <_{\mathcal {L}})$
be a linear order. Let
$\mathcal {L} = (\mathbb {N}, <_{\mathcal {L}})$
be a linear order. Let
![]() $f: [\mathbb {N}]^2 \to 2$
be the coloring defined by
$f: [\mathbb {N}]^2 \to 2$
be the coloring defined by
![]() $f(\{x, y\}) = 1$
iff
$f(\{x, y\}) = 1$
iff
![]() $<_{\mathcal {L}}$
and
$<_{\mathcal {L}}$
and
![]() $<_{\mathbb {N}}$
coincide on
$<_{\mathbb {N}}$
coincide on
![]() $\{x, y\}$
. By the statement of the proposition, there is an infinite set H on which the coloring is semi-hereditary for some color i.
$\{x, y\}$
. By the statement of the proposition, there is an infinite set H on which the coloring is semi-hereditary for some color i.
Before continuing, note that if there is a pair
![]() $x<y\in H$
such that
$x<y\in H$
such that
![]() $f(x, y)=1-i$
then
$f(x, y)=1-i$
then
![]() $\forall z>y\in H, f(x, z)=1-i$
. Indeed, either
$\forall z>y\in H, f(x, z)=1-i$
. Indeed, either
![]() $f(y, z)=1-i$
, in which case by transitivity of
$f(y, z)=1-i$
, in which case by transitivity of
![]() $<_{\mathcal {L}}$
we have
$<_{\mathcal {L}}$
we have
![]() $f(x, z)=1-i$
. Or
$f(x, z)=1-i$
. Or
![]() $f(y, z)=i$
, in which case by semi-heredity
$f(y, z)=i$
, in which case by semi-heredity
![]() $f(x, z)=1-i$
, because otherwise it would imply that
$f(x, z)=1-i$
, because otherwise it would imply that
![]() $f(x, y)=i$
.
$f(x, y)=i$
.
Now if
![]() $\exists ^{\infty } x\in H, \exists y>x\in H, f(x, y)=1-i$
, then we construct an infinite decreasing sequence by induction. Suppose the sequence
$\exists ^{\infty } x\in H, \exists y>x\in H, f(x, y)=1-i$
, then we construct an infinite decreasing sequence by induction. Suppose the sequence
![]() $x_0>_{\mathcal {L}} \ldots >_{\mathcal {L}} x_{n-1}$
has already be constructed, and we have
$x_0>_{\mathcal {L}} \ldots >_{\mathcal {L}} x_{n-1}$
has already be constructed, and we have
![]() $m\in H$
such that
$m\in H$
such that
![]() $f(x_{n-1}, m)=1-i$
, then we look for a
$f(x_{n-1}, m)=1-i$
, then we look for a
![]() $\{x<y\}$
such that
$\{x<y\}$
such that
![]() $x>m$
and
$x>m$
and
![]() $f(x, y)=1-i$
. By the previous remark we have that
$f(x, y)=1-i$
. By the previous remark we have that
![]() $f(x_{n-1}, x)=1-i$
, i.e.,
$f(x_{n-1}, x)=1-i$
, i.e.,
![]() $x_{n+1}>_{\mathcal {L}} x$
, so we extend the sequence with x and redefine
$x_{n+1}>_{\mathcal {L}} x$
, so we extend the sequence with x and redefine
![]() $m\mathrel {\mathop :}= y$
.
$m\mathrel {\mathop :}= y$
.
Else
![]() $\forall ^{\infty } x\in H, \forall y>x\in H, f(x, y)=i$
, and so getting rid of finitely many elements yields an infinite increasing sequence.
$\forall ^{\infty } x\in H, \forall y>x\in H, f(x, y)=i$
, and so getting rid of finitely many elements yields an infinite increasing sequence.
Corollary 6.13. The statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color” implies
![]() $\mathsf {RT}_2^2$
over
$\mathsf {RT}_2^2$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Proof This comes from the fact that
![]() $\mathsf {RT}_2^2\iff S+\mathsf {SHER}$
by definition (with S denoting the statement in question). And we have
$\mathsf {RT}_2^2\iff S+\mathsf {SHER}$
by definition (with S denoting the statement in question). And we have
![]() $\mathsf {RCA}_0\vdash S\implies \mathsf {SHER}$
by using Propositions 4.1, 6.6, and 6.12.
$\mathsf {RCA}_0\vdash S\implies \mathsf {SHER}$
by using Propositions 4.1, 6.6, and 6.12.
Remark 6.14. Let S denote the statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color.” The proof that S implies
![]() $\mathsf {RT}^2_2$
over
$\mathsf {RT}^2_2$
over
![]() $\mathsf {RCA}_0$
involves two applications of S. The first one to obtain an infinite set over which the coloring is semi-hereditary, and a second one to solve
$\mathsf {RCA}_0$
involves two applications of S. The first one to obtain an infinite set over which the coloring is semi-hereditary, and a second one to solve
![]() $\mathsf {SHER}$
using the fact that S implies
$\mathsf {SHER}$
using the fact that S implies
![]() $\mathsf {ADS}$
, which itself implies
$\mathsf {ADS}$
, which itself implies
![]() $\mathsf {SHER}$
. It is unknown whether
$\mathsf {SHER}$
. It is unknown whether
![]() $\mathsf {RT}^2_2$
is computably reducible to S.
$\mathsf {RT}^2_2$
is computably reducible to S.
7 Stable counterparts:
 $\mathsf {SADS}$
and
$\mathsf {SADS}$
and
 ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
Cholak, Jockusch, and Slaman [Reference Cholak, Jockusch and Slaman4] made significant progress in the understanding of Ramsey’s theorem for pairs by dividing the statement into a stable and a cohesive part.
Definition 7.1. A coloring
![]() $f : [\mathbb {N}]^2 \to k$
is stable if for every
$f : [\mathbb {N}]^2 \to k$
is stable if for every
![]() $x \in \mathbb {N}$
,
$x \in \mathbb {N}$
,
![]() $\lim _y f(x, y)$
exists. A linear order
$\lim _y f(x, y)$
exists. A linear order
![]() $\mathcal {L} = (\mathbb {N}, <_{\mathcal {L}})$
is stable if it is of order type
$\mathcal {L} = (\mathbb {N}, <_{\mathcal {L}})$
is stable if it is of order type
![]() $\omega + \omega ^{*}$
.
$\omega + \omega ^{*}$
.
We call
![]() $\mathsf {SRT}^2_k$
and
$\mathsf {SRT}^2_k$
and
![]() $\mathsf {SADS}$
the restriction of
$\mathsf {SADS}$
the restriction of
![]() $\mathsf {RT}^2_k$
and
$\mathsf {RT}^2_k$
and
![]() $\mathsf {ADS}$
to stable colorings and stable linear orders, respectively. Given a linear order
$\mathsf {ADS}$
to stable colorings and stable linear orders, respectively. Given a linear order
![]() $\mathcal {L} = (\mathbb {N}, <_{\mathcal {L}})$
, the coloring corresponding to the order is stable iff the linear order is of order type
$\mathcal {L} = (\mathbb {N}, <_{\mathcal {L}})$
, the coloring corresponding to the order is stable iff the linear order is of order type
![]() $\omega +\omega ^{*}$
, or
$\omega +\omega ^{*}$
, or
![]() $\omega +k$
or
$\omega +k$
or
![]() $k+\omega ^*$
. In particular,
$k+\omega ^*$
. In particular,
![]() $\mathsf {SRT}^2_2$
implies
$\mathsf {SRT}^2_2$
implies
![]() $\mathsf {SADS}$
over
$\mathsf {SADS}$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
In this section, we study the stable counterparts of
![]() ${\mathsf {CAC\ for\ trees}}$
and
${\mathsf {CAC\ for\ trees}}$
and
![]() $\mathsf {SHER}$
, and prove that they are equivalent over
$\mathsf {SHER}$
, and prove that they are equivalent over
![]() $\mathsf {RCA}_0$
. We show
$\mathsf {RCA}_0$
. We show
![]() $\mathsf {SADS}$
implies
$\mathsf {SADS}$
implies
![]() ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
over
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
over
![]() $\mathsf {RCA}_0$
. It follows in particular that every computable instance of
$\mathsf {RCA}_0$
. It follows in particular that every computable instance of
![]() ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
admits a low solution.
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
admits a low solution.
Definition 7.2 (Stable tree, Dorais [Reference Dorais7])
A tree
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
is stable when for every
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
is stable when for every
![]() $\sigma \in T$
either
$\sigma \in T$
either
![]() $\forall ^{\infty }\tau \in T, \sigma \bot \tau $
or
$\forall ^{\infty }\tau \in T, \sigma \bot \tau $
or
![]()
Note that any stable finitely branching tree admits a unique path.
Proposition 7.3.
![]() $\mathsf {RCA}_0\vdash \mathsf {SADS}\implies {\mathsf {CAC\ for\ stable\ c.e.\ trees}}.$
$\mathsf {RCA}_0\vdash \mathsf {SADS}\implies {\mathsf {CAC\ for\ stable\ c.e.\ trees}}.$
Remark 7.4. In the proof below, we use the statement that
![]() $\mathsf {RCA}_0\vdash \mathsf {SADS}\implies \mathsf {B}\Sigma _2^0$
. This is because
$\mathsf {RCA}_0\vdash \mathsf {SADS}\implies \mathsf {B}\Sigma _2^0$
. This is because
![]() $\mathsf {RCA}_0\vdash \mathsf {SADS}\implies \mathsf {PART}$
[Reference Hirschfeldt and Shore13, Proposition 4.6] and
$\mathsf {RCA}_0\vdash \mathsf {SADS}\implies \mathsf {PART}$
[Reference Hirschfeldt and Shore13, Proposition 4.6] and
![]() $\mathsf {RCA}_0\vdash \mathsf {PART}\iff \mathsf {B}\Sigma _2^0$
[Reference Chong, Lempp and Yang5, Theorem 1.2].
$\mathsf {RCA}_0\vdash \mathsf {PART}\iff \mathsf {B}\Sigma _2^0$
[Reference Chong, Lempp and Yang5, Theorem 1.2].
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite c.e. tree which is stable.
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite c.e. tree which is stable.
Consider the total order
![]() $<_0$
, defined by
$<_0$
, defined by
![]() $\sigma <_0\tau \iff \sigma \prec \tau \lor (\sigma \bot \tau \land \sigma (d)<\tau (d))$
where
$\sigma <_0\tau \iff \sigma \prec \tau \lor (\sigma \bot \tau \land \sigma (d)<\tau (d))$
where
![]() $d\mathrel {\mathop :}= \min \{y\mid \sigma (y)\neq \tau (y)\}$
. We show that it is of type
$d\mathrel {\mathop :}= \min \{y\mid \sigma (y)\neq \tau (y)\}$
. We show that it is of type
![]() $\omega +\omega ^*$
, i.e.,
$\omega +\omega ^*$
, i.e.,
So let
![]() $\sigma \in T$
, there are two possibilities. Either
$\sigma \in T$
, there are two possibilities. Either
![]() , meaning we even have
, meaning we even have
![]() $\forall ^{\infty }\tau \in T, \sigma \prec \tau $
, which directly implies
$\forall ^{\infty }\tau \in T, \sigma \prec \tau $
, which directly implies
![]() $\forall ^{\infty }\tau \in T, \sigma <_0\tau $
.
$\forall ^{\infty }\tau \in T, \sigma <_0\tau $
.
Or
![]() $\forall ^{\infty }\tau \in T, \sigma \bot \tau $
. In this case, we consider all the nodes
$\forall ^{\infty }\tau \in T, \sigma \bot \tau $
. In this case, we consider all the nodes
![]() $\tau $
successors of a prefix of
$\tau $
successors of a prefix of
![]() $\sigma $
but not prefix of
$\sigma $
but not prefix of
![]() $\sigma $
, there are finitely many of them, because there are finitely many prefixes of
$\sigma $
, there are finitely many of them, because there are finitely many prefixes of
![]() $\sigma $
and no infinitely-branching node (WLOG, as otherwise there would be a computable infinite antichain). So we can apply the pigeon-hole principle, by using
$\sigma $
and no infinitely-branching node (WLOG, as otherwise there would be a computable infinite antichain). So we can apply the pigeon-hole principle, by using
![]() $\mathsf {B}\Sigma _2^0$
, to deduce that there is a certain
$\mathsf {B}\Sigma _2^0$
, to deduce that there is a certain
![]() $\tau $
which has infinitely many successors.
$\tau $
which has infinitely many successors.
Moreover, by stability of T there cannot be another such node. Indeed, by contradiction, if there were two such nodes
![]() $\tau $
and
$\tau $
and
![]() $\tau '$
, then we would have that
$\tau '$
, then we would have that
![]() $\exists ^{\infty } \eta \in T, \eta \bot \tau $
, because the successors of
$\exists ^{\infty } \eta \in T, \eta \bot \tau $
, because the successors of
![]() $\tau '$
are incomparable to
$\tau '$
are incomparable to
![]() $\tau $
. And since
$\tau $
. And since
![]() $\tau $
already verifies
$\tau $
already verifies
![]() $\exists ^{\infty } \eta \in T, \eta \succ \tau $
, contradicting the stability of T.
$\exists ^{\infty } \eta \in T, \eta \succ \tau $
, contradicting the stability of T.
Therefore we have that
![]() $\forall ^{\infty } \eta \in T, \eta \succ \tau $
, and so depending on whether
$\forall ^{\infty } \eta \in T, \eta \succ \tau $
, and so depending on whether
![]() $\tau <_0\sigma $
or
$\tau <_0\sigma $
or
![]() $\sigma <_0\tau $
, we obtain that
$\sigma <_0\tau $
, we obtain that
![]() $\forall ^{\infty }\eta \in T, \eta <_0\sigma $
or
$\forall ^{\infty }\eta \in T, \eta <_0\sigma $
or
![]() $\forall \eta \in T, \sigma <_0\eta $
, respectively. From there we can apply
$\forall \eta \in T, \sigma <_0\eta $
, respectively. From there we can apply
![]() $\mathsf {SADS}$
and the proof is exactly like in Proposition 4.1.
$\mathsf {SADS}$
and the proof is exactly like in Proposition 4.1.
Corollary 7.5.
![]() ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
admits low solutions.
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}$
admits low solutions.
Proof This comes from the fact that any instance of
![]() $\mathsf {SADS}$
has a low solution, as proven in [Reference Hirschfeldt and Shore13, Theorem 2.11].
$\mathsf {SADS}$
has a low solution, as proven in [Reference Hirschfeldt and Shore13, Theorem 2.11].
The proof that
![]() $\mathsf {SHER}$
follows from
$\mathsf {SHER}$
follows from
![]() ${\mathsf {CAC\ for\ stable\ trees}}$
will use
${\mathsf {CAC\ for\ stable\ trees}}$
will use
![]() $\mathsf {B}\Sigma ^0_2$
. We therefore first prove that
$\mathsf {B}\Sigma ^0_2$
. We therefore first prove that
![]() ${\mathsf {CAC\ for\ stable\ trees}}$
implies
${\mathsf {CAC\ for\ stable\ trees}}$
implies
![]() $\mathsf {B}\Sigma ^0_2$
over
$\mathsf {B}\Sigma ^0_2$
over
![]() $\mathsf {RCA}_0$
.
$\mathsf {RCA}_0$
.
Lemma 7.6.
![]() $\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ stable\ trees}}\implies \forall k, \mathsf {RT}^1_k$
.
$\mathsf {RCA}_0\vdash {\mathsf {CAC\ for\ stable\ trees}}\implies \forall k, \mathsf {RT}^1_k$
.
Proof Let
![]() $f:\mathbb {N}\to k$
be a coloring. There are two possibilities: Either
$f:\mathbb {N}\to k$
be a coloring. There are two possibilities: Either
![]() $\exists i<k, \exists ^{\infty } x, f(x)=i$
, in which case there is an infinite computable f-homogeneous set. Otherwise
$\exists i<k, \exists ^{\infty } x, f(x)=i$
, in which case there is an infinite computable f-homogeneous set. Otherwise
![]() $\forall i<k, \forall ^{\infty } x, f(x)\neq i$
, in which case we consider the infinite tree
$\forall i<k, \forall ^{\infty } x, f(x)\neq i$
, in which case we consider the infinite tree
where
![]() $\mathsf {Inc}$
is the set of strictly increasing strings of
$\mathsf {Inc}$
is the set of strictly increasing strings of
![]() $\mathbb {N}^{<\mathbb {N}}$
.
$\mathbb {N}^{<\mathbb {N}}$
.
By hypothesis, for every node
![]() $\sigma \in T$
,
$\sigma \in T$
,
![]() $\forall ^{\infty } \tau \in T, \sigma \bot \tau $
, otherwise T would have an infinite T-computable path. Thus, T is stable. Moreover, every antichain is of size at most k, thus T is a stable tree with no infinite path and no infinite antichain, contradicting
$\forall ^{\infty } \tau \in T, \sigma \bot \tau $
, otherwise T would have an infinite T-computable path. Thus, T is stable. Moreover, every antichain is of size at most k, thus T is a stable tree with no infinite path and no infinite antichain, contradicting
![]() ${\mathsf {CAC\ for\ stable\ trees}}$
.
${\mathsf {CAC\ for\ stable\ trees}}$
.
Proposition 7.7. Under
![]() $\mathsf {RCA}_0$
the statement
$\mathsf {RCA}_0$
the statement
![]() ${\mathsf {CAC\ for\ stable\ trees}}$
implies
${\mathsf {CAC\ for\ stable\ trees}}$
implies
![]() $\mathsf {SHER}\mathsf {\ for\ stable\ colorings.}$
$\mathsf {SHER}\mathsf {\ for\ stable\ colorings.}$
Proof Let
![]() $f:[\mathbb {N}]^2\to 2$
be a stable coloring, semi-hereditary for the color i. We distinguish two cases. Either there are finitely many integers with limit color i, meaning we can ignore them and use
$f:[\mathbb {N}]^2\to 2$
be a stable coloring, semi-hereditary for the color i. We distinguish two cases. Either there are finitely many integers with limit color i, meaning we can ignore them and use
![]() $\mathsf {B}\Sigma _2^0$
(Lemma 7.6) to compute an infinite homogeneous set (see [Reference Dzhafarov, Hirschfeldt and Reitzes9, Proposition 6.2]). Otherwise there are infinitely many integers whose limit color is i, in which case we use the same proof as in Proposition 6.6, but we must prove the tree T we construct is stable. So let
$\mathsf {B}\Sigma _2^0$
(Lemma 7.6) to compute an infinite homogeneous set (see [Reference Dzhafarov, Hirschfeldt and Reitzes9, Proposition 6.2]). Otherwise there are infinitely many integers whose limit color is i, in which case we use the same proof as in Proposition 6.6, but we must prove the tree T we construct is stable. So let
![]() $\sigma _n$
be a node of this tree.
$\sigma _n$
be a node of this tree.
Suppose first n has limit color i. Let p be sufficiently large so that
![]() $f(n, p) = i$
. As explained in Proposition 6.6,
$f(n, p) = i$
. As explained in Proposition 6.6,
![]() $\sigma _p$
contains all the integers
$\sigma _p$
contains all the integers
![]() $m < p$
such that
$m < p$
such that
![]() $f(m, p) = i$
. It follows that
$f(m, p) = i$
. It follows that
![]() $n \in \sigma _p$
. Moreover, if
$n \in \sigma _p$
. Moreover, if
![]() $n \in \sigma _p$
, then
$n \in \sigma _p$
, then
![]() $\sigma _n \preceq \sigma _p$
. Thus,
$\sigma _n \preceq \sigma _p$
. Thus,
![]() $\forall ^{\infty } p, \sigma _n\prec \sigma _p$
.
$\forall ^{\infty } p, \sigma _n\prec \sigma _p$
.
Suppose now n has limit color
![]() $1-i$
, then since there are infinitely many integers with limit color i, there is one such that
$1-i$
, then since there are infinitely many integers with limit color i, there is one such that
![]() $p>n$
. In particular,
$p>n$
. In particular,
![]() $\sigma _p$
verifies
$\sigma _p$
verifies
![]() $\forall ^{\infty } \tau \in T, \sigma _p\prec \tau $
. Thus, if
$\forall ^{\infty } \tau \in T, \sigma _p\prec \tau $
. Thus, if
![]() $\sigma _n\prec \sigma _p$
then
$\sigma _n\prec \sigma _p$
then
![]() $\forall ^{\infty } \tau \in T, \sigma _n\prec \tau $
, and if
$\forall ^{\infty } \tau \in T, \sigma _n\prec \tau $
, and if
![]() $\sigma _n\bot \sigma _p$
then
$\sigma _n\bot \sigma _p$
then
![]() $\forall ^{\infty } \tau \in T, \sigma _n\bot \tau $
.
$\forall ^{\infty } \tau \in T, \sigma _n\bot \tau $
.
Proposition 7.8. Under
![]() $\mathsf {RCA}_0$
the statement
$\mathsf {RCA}_0$
the statement
![]() $\mathsf {SHER}\mathsf {\ for\ stable\ colorings}$
implies
$\mathsf {SHER}\mathsf {\ for\ stable\ colorings}$
implies
![]() ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}.$
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}.$
Proof Let
![]() $T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite stable c.e. tree. The proof is the same as in Proposition 6.3, but we must verify that the coloring
$T\subseteq \mathbb {N}^{<\mathbb {N}}$
be an infinite stable c.e. tree. The proof is the same as in Proposition 6.3, but we must verify that the coloring
![]() $f:[\mathbb {N}]^2\to 2$
defined is stable. Given
$f:[\mathbb {N}]^2\to 2$
defined is stable. Given
![]() $x\in \mathbb {N}$
, we claim that
$x\in \mathbb {N}$
, we claim that
![]() $\exists i<2, \forall ^{\infty } y f(x, y)=i$
. Since T is stable, either
$\exists i<2, \forall ^{\infty } y f(x, y)=i$
. Since T is stable, either
![]() or
or
![]() $\forall ^{\infty } y, \psi (x)\bot \psi (y)$
holds. In the first case
$\forall ^{\infty } y, \psi (x)\bot \psi (y)$
holds. In the first case
![]() $\forall ^{\infty } y, f(x, y)=1$
, and in the second one
$\forall ^{\infty } y, f(x, y)=1$
, and in the second one
![]() $\forall ^{\infty } y, f(x, y)=0$
. Thus the coloring is stable, and the proof can be carried on.
$\forall ^{\infty } y, f(x, y)=0$
. Thus the coloring is stable, and the proof can be carried on.
Corollary 7.9. The following are equivalent over
![]() $\mathsf {RCA}_0$
:
$\mathsf {RCA}_0$
:
-
(1)
 ${\mathsf {CAC\ for\ stable\ trees}}.$
${\mathsf {CAC\ for\ stable\ trees}}.$
-
(2)
 ${\mathsf {CAC\ for\ stable\ c.e.\ trees}}.$
${\mathsf {CAC\ for\ stable\ c.e.\ trees}}.$
-
(3)
 $\mathsf {SHER}\mathsf {\ for\ stable\ colorings.}$
$\mathsf {SHER}\mathsf {\ for\ stable\ colorings.}$
8 Conclusion
The following figure sums up the implications proved in this paper. All implications hold both in
![]() $\mathsf {RCA}_0$
and over the computable reduction.
$\mathsf {RCA}_0$
and over the computable reduction.

We have established in Theorem 2.5 the equivalence between
![]() $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
and other statements.
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
and other statements.
Question 8.1. What is the first-order part of
![]() $\mathsf {TAC}$
?
$\mathsf {TAC}$
?
Recall that, by Corollary 5.3, for every fixed low set X, there is a computable instance of
![]() $\mathsf {TAC}$
with no X-computable solution. By computable equivalence, this property also holds for
$\mathsf {TAC}$
with no X-computable solution. By computable equivalence, this property also holds for
![]() ${\mathsf {CAC\ for\ trees}}$
. It is however unknown whether Corollary 5.3 can be improved to defeat all low sets simultaneously.
${\mathsf {CAC\ for\ trees}}$
. It is however unknown whether Corollary 5.3 can be improved to defeat all low sets simultaneously.
Question 8.2. Does every computable instance of
![]() ${\mathsf {CAC\ for\ trees}}$
admit a low solution?
${\mathsf {CAC\ for\ trees}}$
admit a low solution?
Note that by Corollary 7.5, any negative witness to the previous question would yield a non-stable tree.
We have also seen by Proposition 3.11 that for every computable instance T of
![]() ${\mathsf {CAC\ for\ trees}}$
, every computably bounded
${\mathsf {CAC\ for\ trees}}$
, every computably bounded
![]() $\mathsf {DNC}$
function relative to
$\mathsf {DNC}$
function relative to
![]() $\emptyset '$
computes a solution to T. The natural question would be whether we can improve this result to any
$\emptyset '$
computes a solution to T. The natural question would be whether we can improve this result to any
![]() $\mathsf {DNC}$
function relative to
$\mathsf {DNC}$
function relative to
![]() $\emptyset '$
.
$\emptyset '$
.
Question 8.3. Is there some X such that for every computable instance T of
![]() ${\mathsf {CAC\ for\ trees}}$
, every
${\mathsf {CAC\ for\ trees}}$
, every
![]() $\mathsf {DNC}$
function relative to X computes a solution to T?
$\mathsf {DNC}$
function relative to X computes a solution to T?
Note that in the case of a computable set X, the answer is negative, as there exist
![]() $\mathsf {DNC}$
functions of low degree.
$\mathsf {DNC}$
functions of low degree.
Finally, recall from Remark 6.14 the following question:
Question 8.4. Is
![]() $\mathsf {RT}_2^2$
computably reducible to the statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color”?
$\mathsf {RT}_2^2$
computably reducible to the statement “for any 2-coloring of pairs, there exists an infinite set which is semi-hereditary for some color”?
Acknowledgments
This project started as the study of Ramsey-like theorems for 3-variable forbidden patterns. The attempt to prove Corollary 6.13 naturally led to the study of the
![]() $\mathsf {SHER}$
principle, already defined by Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8]. Thanks to multiple personal communications with François Dorais, we realized that the
$\mathsf {SHER}$
principle, already defined by Dorais et al. [Reference Dorais, Dzhafarov, Hirst, Mileti and Shafer8]. Thanks to multiple personal communications with François Dorais, we realized that the
![]() $\mathsf {SHER}$
principle is closely related to trees, and more precisely, equivalent to the chain–antichain principle for trees, a principle studied by Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3]. We later realized that
$\mathsf {SHER}$
principle is closely related to trees, and more precisely, equivalent to the chain–antichain principle for trees, a principle studied by Binns et al. in [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3]. We later realized that
![]() $\mathsf {SHER}$
is also equivalent to
$\mathsf {SHER}$
is also equivalent to
![]() $\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
, where
$\mathsf {TAC}+\mathsf {B}\Sigma ^0_2$
, where
![]() $\mathsf {TAC}$
is an antichain principle for completely branching c.e. trees, defined by Conidis [Reference Conidis6]. Some of the results are therefore independent rediscoveries of some theorems from [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Reference Conidis6], but in a more unified setting. The authors are thankful to Chris Conidis, François Dorais, and Alberto Marcone for interesting comments and discussions. The authors are also thankful to the anonymous referee for his careful reading and his numerous improvement suggestions.
$\mathsf {TAC}$
is an antichain principle for completely branching c.e. trees, defined by Conidis [Reference Conidis6]. Some of the results are therefore independent rediscoveries of some theorems from [Reference Binns, Kjos-Hanssen, Lerman, Schmerl and Solomon3, Reference Conidis6], but in a more unified setting. The authors are thankful to Chris Conidis, François Dorais, and Alberto Marcone for interesting comments and discussions. The authors are also thankful to the anonymous referee for his careful reading and his numerous improvement suggestions.
Funding
The authors were partially supported by grant ANR “ACTC” #ANR-19-CE48-0012-01.