Published online by Cambridge University Press: 04 April 2023
We refine results of Gannon [6, Theorem 4.7] and Simon [22, Lemma 2.8] on convergence of Morley sequences. We then introduce the notion of eventual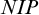 $NIP$, as a property of a model, and prove a variant of [15, Corollary 2.2]. Finally, we give new characterizations of generically stable types (for countable theories) and reinforce the main result of Pillay [17] on the model-theoretic meaning of Grothendieck’s double limit theorem.
$NIP$, as a property of a model, and prove a variant of [15, Corollary 2.2]. Finally, we give new characterizations of generically stable types (for countable theories) and reinforce the main result of Pillay [17] on the model-theoretic meaning of Grothendieck’s double limit theorem.
Dedicated to the memory of my first teacher Fatemeh Mardani