Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-17T23:19:28.422Z Has data issue: false hasContentIssue false
  • English
  • Français

Remark on Nicod's reduction of Principia mathematica

Published online by Cambridge University Press:  12 March 2014

B. A. Bernstein
B. A. Bernstein*
Affiliation:
The University of California, Berkeley, California
Get access Rights & Permissions [Opens in a new window]

Extract

The object of this note is to close a slight gap, hitherto seemingly over-looked, in Nicod's derivation from his postulates of the primitives of Principia mathematica. The gap consists in this: Nicod's propositions corresponding to *1·1−*1·6 of the Principia, though they bear the same names and have the same symbol-forms as the Principia propositions, are not precisely *1·1−1·6. Indeed, if we denote Nicod's “p ⊃ q” and “p · q” by “p < q” and “pq” respectively, and if we write p′ for p∣p and p″ for (p′)′ then in terms of the “stroke,” we have

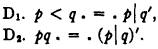
But p ⊃ q and p · q of the Principia are

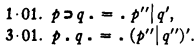
Accordingly, the Nicod-Principia propositions are not *1·1−*1·6. They are *1·1−*1·6 in which < takes the place of ⊃, and Nicod has not shown us explicitly how to pass from < to ⊃.

It is true that Nicod also proves the following:

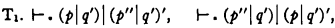
i.e.,

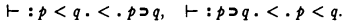
This yields: If ⊢· p < q then ⊢· p ⊃ q, and conversely. This would seem to allow passing from < to ⊃ throughout a proposition. But, it is clear, T1 permits this change only in the case of the principal <. The change in the case of a minor < still has to be justified.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 2 , Issue 4 , December 1937 , pp. 165 - 166
Copyright
Copyright © Association for Symbolic Logic 1937

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1 Nicod, J. G. P., Proceedings of the Cambridge Philosophical Society, vol. 19 (1917), pp. 32–41 Google Scholar.

2 The proposition corresponding to * 1 · 1 is not given explicitly by Nicod.

3 There is no essential difference between a “rule” and a “postulate” in the Principia propositions * 1 · 1− * 1 · 71. The theory of deduction of the Principia seems to contain no “rule” except * 1 · 1. But * 3·03 is a “rule,” and the authors might have obtained other “rules” ad libitum. For other “rules” derived from the primitives of the Principia see Proceedings of the Cambridge Philosophical Society, vol. 28 (1932), pp. 427–432 CrossRefGoogle Scholar.

4 Jørgensen, J., A treatise of formal logic, Copenhagen and London 1931, Vol. II, Chap. VIIGoogle Scholar.