Article contents
Relativised quantification: Some canonical varieties of sequence-set algebras
Published online by Cambridge University Press: 12 March 2014
Extract
This paper explores algebraic aspects of two modifications of the usual account of first-order quantifiers.
Standard first-order quantificational logic is modelled algebraically by cylindric algebras. Prime examples of these are algebras whose members are sets of sequences: given a first-order model U for a language that is based on the set {υκ: κ < α} of variables, each formula φ is represented by the set
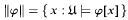
of all those α-length sequences x = 〈xκ: κ < α〉 that satisfy φ in U. Such a sequence provides a value-assignment to the variables (υκ is assigned value xκ), but it may also be viewed geometrically as a point in the α-dimensional Cartesian spaceαU of all α-length sequences whose terms come from the underlying set U of U. Then existential quantification is represented by the operation of cylindrification. To explain this, define a binary relation Tκ on sequences by putting xTκy if and only if x and y differ at most at their κth coordinate, i.e.,
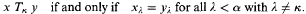
Then for any set X ⊆ αU, the set
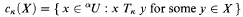
is the “cylinder” generated by translation of X parallel to the κth coordinate axis in αU. Given the standard semantics for the existential quantifier ∃υκ as
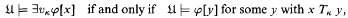
it is evident that
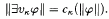
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 4
- Cited by


