Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T18:15:25.810Z Has data issue: false hasContentIssue false
  • English
  • Français

RELATIVELY EXCHANGEABLE STRUCTURES

Published online by Cambridge University Press:  01 August 2018

HARRY CRANE  and
HENRY TOWSNER
HARRY CRANE
Affiliation:
DEPARTMENT OF STATISTICS & BIOSTATISTICS RUTGERS UNIVERSITY 110 FRELINGHUYSEN AVENUE, PISCATAWAY NJ 08854, USAE-mail:[email protected]: http://stat.rutgers.edu/home/hcrane
HENRY TOWSNER
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF PENNSYLVANIA 209 SOUTH 33RD STREET, PHILADELPHIA PA 19104-6395, USAE-mail:[email protected]: http://www.math.upenn.edu/∼htowsner
Get access Rights & Permissions [Opens in a new window]

Abstract

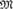We study random relational structures that are relatively exchangeable—that is, whose distributions are invariant under the automorphisms of a reference structure ${M}$. When 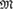${M}$ is ultrahomogeneous and has trivial definable closure, all random structures relatively exchangeable with respect to 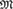$m$ satisfy a general Aldous–Hoover-type representation. If 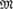${M}$ also satisfies the n-disjoint amalgamation property (n-DAP) for all 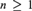$n \ge 1$, then relatively exchangeable structures have a more precise description whereby each component depends locally on 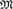${M}$.

Keywords

03C0703C9860G09exchangeabilityAldous–Hoover theoremrelational structureFraïsse limitamalgamation
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 416 - 442
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ackerman, N., Representations of ${\rm{Aut(m)}}$-invariant measures: Part 1, 2015, arXiv:1509.06170.Google Scholar
Ackerman, N., Freer, C., Kwiatkowska, A., and Patel, R., A classification of orbits admitting a unique invariant measure. Annals of Pure and Applied Logic, vol. 168 (2017), no. 1, pp. 19–36.CrossRefGoogle Scholar
Ackerman, N., Freer, C., Nešetřil, J., and Patel, R., Invariant measures via inverse limits of finite structures. European Journal of Combinatorics, vol. 52 (2016), no. part B, pp. 248–289.CrossRefGoogle Scholar
Ackerman, N., Freer, C., and Patel, R., Invariant measures concentrated on countable structures. Forum of Mathematics, Sigma, vol. 4 (2016), pp. e17–e59.CrossRefGoogle Scholar
Aldous, D. J., Representations for partially exchangeable arrays of random variables. Journal of Multivariate Analysis, vol. 11 (1981), no. 4, pp. 581–598.CrossRefGoogle Scholar
Aldous, D. J., Exchangeability and related topics, École d’été de probabilités de Saint-Flour, XIII—1983 (Hennequin, P. L., editor), Lecture Notes in Mathematics, vol. 1117, Springer, Berlin, 1985, pp. 1–198.CrossRefGoogle Scholar
Aroskar, A. and Cummings, J., Limits, regularity and removal for finite structures, 2014, arXiv:1412.8084v1.Google Scholar
Austin, T. and Panchenko, D., A hierarchical version of the de Finetti and Aldous–Hoover representations. Probability Theory and Related Fields, vol. 159 (2014), no. 3–4, pp. 809–823.CrossRefGoogle Scholar
Bertoin, J., Random Fragmentation and Coagulation Processes, Cambridge Studies in Advanced Mathematics, vol. 102, Cambridge University Press, Cambridge, 2006.CrossRefGoogle Scholar
Brooke-Taylor, A. and Testa, D., The infinite random simplicial complex, 2013, arXiv:1308.5517.Google Scholar
Crane, H., The cut-and-paste process. Annals of Probability, vol. 42 (2014), no. 5, pp. 1952–1979.CrossRefGoogle Scholar
Crane, H., Dynamic random networks and their graph limits. Annals of Applied Probability, vol. 26 (2016), no. 2, pp. 691–721.CrossRefGoogle Scholar
Crane, H., Exchangeable graph-valued Feller processes. Probability Theory and Related Fields, vol. 168 (2016), pp. 849–899.CrossRefGoogle Scholar
Crane, H. and Towsner, H., The structure of combinatorial Markov processes, 2015, arXiv:1603.05954.Google Scholar
de Finetti, B, La prévision: ses lois logiques, ses sources subjectives. Annales de l’Institut Henri Poincaré, vol. 7 (1937), pp. 1–68Google Scholar
Diaconis, P. and Janson, S., Graph limits and exchangeable random graphs. Rendiconti di Matematica e delle sue Applicazioni. Serie VII, vol. 28 (2008), no. 1, pp. 33–61.Google Scholar
Hoover, D. N., Relations on Probability Spaces and Arrays of Random Variables, Institute for Advanced Studies, preprint, 1979. Available online at https://www.stat.berkeley.edu/∼aldous/Research/hoover.pdf.Google Scholar
Kallenberg, O., Probabilistic Symmetries and Invariance Principles, Probability and its Applications, Springer, New York, 2005.Google Scholar
Kingman, J. F. C., Random partitions in population genetics. Proceedings of the Royal Society of London, Series A: Mathematical, Physical and Engineering Sciences, vol. 361 (1978), no. 1704, pp. 1–20.CrossRefGoogle Scholar
Kruckman, A., Disjoint n-amalgamation and pseudofinite countably categorical theories, 2015, arXiv:1510.03539.Google Scholar
Lovász, L. and Szegedy, B., Limits of dense graph sequences. Journal of Combinatorial Theory, Series B, vol. 96 (2006), pp. 933–957.CrossRefGoogle Scholar
Macpherson, D., A survey of homogeneous structures. Discrete Mathematics, vol. 311 (2011), pp. 1599–1634.CrossRefGoogle Scholar
Petrov, F. and Vershik, A., Uncountable graphs and invariant measures on the set of universal countable graphs. Random Structures & Algorithms, vol. 37 (2010), no. 3, pp. 389–406.CrossRefGoogle Scholar
Pitman, J., Combinatorial Stochastic Processes, Lecture Notes in Mathematics, vol. 1875, Springer-Verlag, Berlin, 2006, Lectures from the 32nd Summer School on Probability Theory held in Saint-Flour, July 7–24, 2002.Google Scholar