Published online by Cambridge University Press: 22 June 2020
We study large cardinal properties associated with Ramseyness in which homogeneous sets are demanded to satisfy various transfinite degrees of indescribability. Sharpe and Welch [25], and independently Bagaria [1], extended the notion of 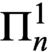 $\Pi ^1_n$
-indescribability where
$\Pi ^1_n$
-indescribability where 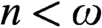 $n<\omega $
to that of
$n<\omega $
to that of 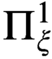 $\Pi ^1_\xi $
-indescribability where
$\Pi ^1_\xi $
-indescribability where 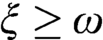 $\xi \geq \omega $
. By iterating Feng’s Ramsey operator [12] on the various
$\xi \geq \omega $
. By iterating Feng’s Ramsey operator [12] on the various 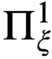 $\Pi ^1_\xi $
-indescribability ideals, we obtain new large cardinal hierarchies and corresponding nonlinear increasing hierarchies of normal ideals. We provide a complete account of the containment relationships between the resulting ideals and show that the corresponding large cardinal properties yield a strict linear refinement of Feng’s original Ramsey hierarchy. We isolate Ramsey properties which provide strictly increasing hierarchies between Feng’s
$\Pi ^1_\xi $
-indescribability ideals, we obtain new large cardinal hierarchies and corresponding nonlinear increasing hierarchies of normal ideals. We provide a complete account of the containment relationships between the resulting ideals and show that the corresponding large cardinal properties yield a strict linear refinement of Feng’s original Ramsey hierarchy. We isolate Ramsey properties which provide strictly increasing hierarchies between Feng’s 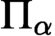 $\Pi _\alpha $
-Ramsey and
$\Pi _\alpha $
-Ramsey and 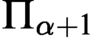 $\Pi _{\alpha +1}$
-Ramsey cardinals for all odd
$\Pi _{\alpha +1}$
-Ramsey cardinals for all odd 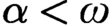 $\alpha <\omega $
and for all
$\alpha <\omega $
and for all 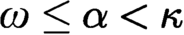 $\omega \leq \alpha <\kappa $
. We also show that, given any ordinals
$\omega \leq \alpha <\kappa $
. We also show that, given any ordinals 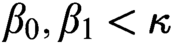 $\beta _0,\beta _1<\kappa $
the increasing chains of ideals obtained by iterating the Ramsey operator on the
$\beta _0,\beta _1<\kappa $
the increasing chains of ideals obtained by iterating the Ramsey operator on the 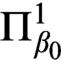 $\Pi ^1_{\beta _0}$
-indescribability ideal and the
$\Pi ^1_{\beta _0}$
-indescribability ideal and the 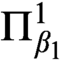 $\Pi ^1_{\beta _1}$
-indescribability ideal respectively, are eventually equal; moreover, we identify the least degree of Ramseyness at which this equality occurs. As an application of our results we show that one can characterize our new large cardinal notions and the corresponding ideals in terms of generic elementary embeddings; as a special case this yields generic embedding characterizations of
$\Pi ^1_{\beta _1}$
-indescribability ideal respectively, are eventually equal; moreover, we identify the least degree of Ramseyness at which this equality occurs. As an application of our results we show that one can characterize our new large cardinal notions and the corresponding ideals in terms of generic elementary embeddings; as a special case this yields generic embedding characterizations of 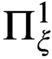 $\Pi ^1_\xi $
-indescribability and Ramseyness.
$\Pi ^1_\xi $
-indescribability and Ramseyness.