Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T20:33:53.744Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduced products and nonstandard logics1

Published online by Cambridge University Press:  12 March 2014

M. Benda
M. Benda*
Affiliation:
University of Wisconsin, Madison
Get access Rights & Permissions [Opens in a new window]

Extract

The results of the present paper were announced in [1]. The work is divided into our parts. In the first part we define relations 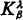(relations between relational struc tures) and we show their connection with the equivalence of the languages LΚ,λ (Theorem 1). The relations 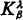generalize the games Gn (n < ω) of Ehrenfeucht (see [2]) and the conditions (i)–(ii) which were used by Karp in [5].

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 34 , Issue 3 , 17 November 1969 , pp. 424 - 436
Copyright
Copyright © Association for Symbolic Logic 1969

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

I wish to express my gratitude to Prof. A. Mostowski who greatly encouraged me during the preparation of this paper.

References

[1]Benda, M., Ultraproducts and non-standard logics, Bulletin de l'Académie Polonaise des Sciences, vol. XVI (1968), No. 6.Google Scholar
[2]Ehrenfeucht, A., An application of games to the completeness problem for formalized theories, Fundamenta Mathematicae, vol. 49 (1960), p. 129.CrossRefGoogle Scholar
[3]Feferman, S. and Vaught, R. L., The first order properties of products of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), p. 57.CrossRefGoogle Scholar
[4]Frayne, T., Morel, A. C. and Scott, S. C., Reduced direct products, Fundamenta Mathematicae, vol. 51 (1962), p. 195.CrossRefGoogle Scholar
[5]Karp, C. R., Finite quantifier equivalence, The theory of models, North-Holland, Amsterdam, 1965, p. 407.Google Scholar
[6]Karp, C. R., Languages with expressions of infinite length, North-Holland, Amsterdam, 1964.Google Scholar
[7]Keisler, H. J., Ultraproducts and elementary classes, Indagationes Mathematicae, vol. 23 (1962), p. 447.Google Scholar
[8]Keisler, H. J., Ultraproducts and saturated models, Indagationes Mathematicae, vol. 26 (1964), p. 178.CrossRefGoogle Scholar
[9]Kochen, S., Ultraproducts in the theory of models, Annals of Mathematics, vol. 74 (1961), p. 221.CrossRefGoogle Scholar