Published online by Cambridge University Press: 12 March 2014
A primitive-recursive sequence of rational numbers sn is said to be primitive-recursively irrational, if there are primitive recursive functions n(k), i(p, q) > 0 and N(p, q) such that:
1. (k)(n ≥ n(k) → ∣sn – sn(k)∣ < 2−k).
2. (p)(q)(q > 0 & n ≥ N(p, q) → ∣sn ± p/q∣ > 1/i(p, q)).
The object of the present note is to establish the primitive-recursive irrationality of a sequence which converges to π. In a previous paper we proved the primitive-recursive irrationality of the exponential series Σxn/n!, for all rational values of x, and showed that a primitive-(general-) recursively irrational sequence sn is strongly primitive-(general-)recursive convergent in any scale, where a recursive sequence sn is said to be strongly primitive-(general-)recursive convergent in the scale r (r ≥ 2), if there is a non-decreasing primitive-(general-) recursive function r(k) such that
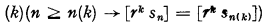 ,
,
where [x] is the greatest integer contained in x, i.e. [x] = i if i ≤ x < i + 1, [x] = —i if i ≤ —x < i+1, where i is a non-negative integer.
A rational recursive sequence sn is said to be recursive convergent, if there is a recursive function n(k) such that
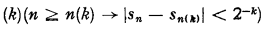 .
.
If a sequence sn is strongly recursive convergent in a scale r, then it is recursive convergent and its limit is the recursive real number 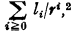 where, for any k ≥ 0,
where, for any k ≥ 0,
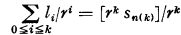 .
.
1 The strong convergence of the exponential function, Journal of the London Mathematical Society, vol. 22 (1947), pp. 200–205Google Scholar.
2 Loc. cit., p. 204.
3 Grundlagen der Mathematik, vol. 2 (1939), Berlin (Springer), p. 279Google Scholar.