Article contents
Recursive functions in basic logic
Published online by Cambridge University Press: 12 March 2014
Extract
1.1 The system K* of basic logic, as presented in a previous paper, will be shown to be formalizable in an alternative way according to which the rule [E],
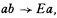
is replaced by the rule [F],
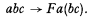
1.2. General recursive functions will be shown to be definable in K* in a way that retains functional notation, so that the equation,
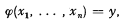
will be formalized in K* by the formula,
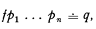
where ‘f’, ‘p1’, … ‘pn’ respectively denote φ, x1, …, xn, and where ‘≐’ plays the role of numerical equality. Partial recursive functions may be handled in a similar way. The rule [E] is not required for dealing with primitive recursive functions by this method.
1.3. An operator ‘G’ will be defined such that ‘[Ga ≐ p]’ is a theorem of K* if and only if ‘p’ denotes the Gödel number of ‘a’.
1.4. In reformulating K* we assume ‘o0’, ‘o1,’ ‘o2’, …, have been so chosen that we can determine effectively whether or not a given U-expression is the mth member of the above series. The revised rules for K* are then as follows. (Double-arrow forms of these rules are derivable, except in the case of rule [V].)
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1956
References
1 Fitch, F. B., A simplification of basic logic, this Journal, vol. 18 (1953), pp. 317–325Google Scholar. This paper will be referred to as SBL. Closely related to it are my two papers, A definition of negation in extended basic logic, ibid. vol. 19 (1954), pp. 29–36, referred to as DN, and Self-referential relations, Actes du XIème Congrès International de Philosophie, vol. 14, pp. 121–127, Amsterdam, 1953Google Scholar. The above papers are based on my following three earlier papers: A basic logic, this Journal, vol. 7 (1942), pp. 105–114Google Scholar, referred to as BL; Representations of calculi, this Journal, vol. 9 (1944), pp. 57–62Google Scholar, referred to as RC; An extension of basic logic, this Journal, vol. 13 (1948), pp. 95–106Google Scholar.
2 A method not retaining functional notation was given in RC. Some well-known properties of general recursive functions are presupposed in what follows. In connection with the theory of general recursive functions see Kleene, S. C., Introduction to metamathematics, Amsterdam, 1952Google Scholar.
- 4
- Cited by


