Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-22T20:55:27.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursion theory on orderings. I. A model theoretic setting1

Published online by Cambridge University Press:  12 March 2014

G. Metakides  and
J.B. Remmel
G. Metakides
Affiliation:
University of Rochester, Rochester, New York 14627
J.B. Remmel
Affiliation:
University of California at San Diego, La Jolla, California 92037
Get access Rights & Permissions [Opens in a new window]

Extract

In [6], Metakides and Nerode introduced the study of the lattice of recursively enumerable substructures of a recursively presented model as a means to understand the recursive content of certain algebraic constructions. For example, the lattice of recursively enumerable subspaces, 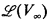, of a recursively presented vector space V∞ has been studied by Kalantari, Metakides and Nerode, Retzlaff, Remmel and Shore. Similar studies have been done by Remmel [12], [13] for Boolean algebras and by Metakides and Nerode [9] for algebraically closed fields. In all of these models, the algebraic closure of a set is nontrivial. (The formal definition of the algebraic closure of a set S, denoted cl(S), is given in §1, however in vector spaces, cl(S) is just the subspace generated by S, in Boolean algebras, cl(S) is just the subalgebra generated by S, and in algebraically closed fields, cl(S) is just the algebraically closed subfield generated by S.)

In this paper, we give a general model theoretic setting (whose precise definition will be given in §1) in which we are able to give constructions which generalize many of the constructions of classical recursion theory. One of the main features of the models 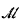which we study is that the algebraic closure of set 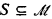is just itself, i.e., cl(S) = S. Examples of such models include the natural numbers under equality 〈N, = 〉, the rational numbers under the usual ordering 〈Q, ≤〉, and a large class of n-dimensional partial orderings.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 3 , September 1979 , pp. 383 - 402
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

We wish to acknowledge many helpful conversations with A. Nerode.

2

Supported under NSF Grant MCS77–0421.

References

REFERENCES

[1]Dekker, J. C. E.. A theorem on hypersimple sets, Proceedings of the American Mathematical Society, vol. 5 (1954), pp. 791–796.CrossRefGoogle Scholar
[2]Friedberg, R. M., Three theorems on recursive enumeration, I, Decomposition, II, Maximal sets, III, Enumeration without duplication, this Journal, vol. 23 (1958), pp. 309–316.Google Scholar
[3]Lachlan, A. H., On the lattice of recursively enumerable sets, Transactions of the American Mathematical Society, vol. 130 (1968), pp. 1–27.CrossRefGoogle Scholar
[4]Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
[5]Manaster, A. B. and Remmel, J. B., ℵ0-categorical dense n-dimensional partial orderings (in preparation).Google Scholar
[6]Metakides, G. and Nerode, A., Recursion theory and algebra, Algebra and Logic, Lecture Notes in Mathematics, vol. 450 (1975), Springer-Verlag, Berlin and New York, pp. 209–219.CrossRefGoogle Scholar
[7]Metakides, G., Recursively enumerable vector spaces, Annals of Mathematical Logic, vol. 11 (1977), pp. 147–172.CrossRefGoogle Scholar
[8]Metakides, G., Creative presentations, Notices of the American Mathematica Society, vol. 21 (1947), p. A–551.Google Scholar
[9]Metakides, G., Recursion theory on fields (in preparation).Google Scholar
[10]Morley, M. D. and Soare, R., Boolean algebras, splitting theorems, and Δ20 sets, Fundamenta Mathematicae, vol. 90 (1975), pp. 45–51.CrossRefGoogle Scholar
[11]Myhill, J., Creative sets, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 1 (1955), pp. 97–108.CrossRefGoogle Scholar
[12]Remmel, J. B., Recursively enumerable Boolean algebras, Annals of Mathematical Logic, vol. 15 (1978), pp. 75–106.CrossRefGoogle Scholar
[13]Remmel, J. B., R-maximal Boolean algebras, this Journal (to appear).Google Scholar
[14]Remmel, J. B., Recursion theory on orderings. II, this Journal (to appear).Google Scholar
[15]Robinson, R. W., Simplicity of recursively enumerable sets, this Journal, vol. 32 (1967), pp. 162–172.Google Scholar
[16]Rogers, H. J. Jr.Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[17]Yates, C. E. M., Three theorems on the degrees of recursively enumerable sets, Duke Mathematical Journal, vol. 32 (1965), pp. 461–468.CrossRefGoogle Scholar