Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-25T01:47:06.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursion in Kolmogorov's R-operator and the ordinal σ3

Published online by Cambridge University Press:  12 March 2014

Thomas John
Thomas John*
Affiliation:
Department of Mathematics, Ohio State University, Columbus, Ohio 43210
*
Deparment of Mathematical Sciences, South Dakota School of Mines and Technology, Rapid City, South Dakota 57701-3995
Get access Rights & Permissions [Opens in a new window]

Extract

The theory of objects recursive in functions of higher types was developed originally by Kleene [Kl 1,2]. The sets of objects of finite types are defined by Kleene as follows:

T0 = ω = the set of nonnegative integers,

and, for all i ∈ ω,

Ti+1 = Tiω = the set of total functions from Ti to ω.

In order to study and classify the functions recursive in Kolmogorov's R-operator, it is necessary to discuss recursion in partial functions of higher types. Accordingly, we define the partial objects of higher finite types by

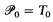
and, for all i ∈ ω,

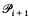= the set of partial functions from Ti to ω.

In addition to considering the partial functions from Ti to ω, the “hereditary partial” functions also have to be considered. For example, Hinman has studied objects of type 2 which act on partial functions from ω to ω. In case of dealing with a function F which has partial functions in its domain, we usually require that F be consistent, i.e. if F(f) is defined and g is an object of the same type as f, defined at least at all points where f is defined (in short, g extends f—notation: g ⊇ f), then F(g) is defined and is equal to F(f). Now we can define the higher type partial objects which are consistent by

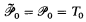
and, for all i ∈ ω,

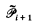= the set of consistent partial functions from 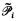to ω.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 1 , March 1986 , pp. 1 - 11
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCE

[Ac 1]Aczel, P., Representability in some systems of second order arithmetic, Israel Journal of Mathematics, vol. 8 (1970), pp. 309–328.Google Scholar
[Ac 2]Aczel, P., Quantifiers, games and inductive definitions, Proceedings of the third Scandinavian logic symposium (Kanger, S., editor), North-Holland, Amsterdam, 1975, pp. 1–14.Google Scholar
[Ce 1]Cenzer, D., Ordinal recursion and inductive definitions, Generalized recursion theory (Fenstad, J. E. and Hinman, P. G., editors), North-Holland, Amsterdam, 1974, pp. 221–264.Google Scholar
[Ha 1]Harrington, L., Kolmogorov's R-operator and the first nonprojectible ordinal, handwritten notes, 07, 1975(13 pp.)Google Scholar
[Ha 2]Harrington, L., Contributions to recursion theory on higher types, Ph.D. thesis, Massachusetts Institute of Technology, Cambridge, Massachusetts, 1973.Google Scholar
[Hi 1]Hinman, P. G., Hierarchies of effective descriptive set theory, Transactions of the American Mathematical Society, vol. 142 (1969), pp. 111–140.CrossRefGoogle Scholar
[Kl 1]Kleene, S. C., Recursive functional and quantifiers of finite types. I, Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
[Kl 2]Kleene, S. C., Recursive functionals and quantifiers of finite types. II, Transactions of the American Mathematical Society, vol. 108 (1963), pp. 106–142.Google Scholar
[KM 1]Kechris, A. and Moschovakis, Y., Recursion in higher types, Handbook of mathematical logic (Barwise, J., editor), North-Holland, Amsterdam, 1977, pp. 681–737.Google Scholar
[Mo 1]Moschovakis, Y., Descriptive set theory, North-Holland, Amsterdam, 1980.Google Scholar
[Mo 2]Moschovakis, Y., Hyperanalytic predicates, Transactions of the American Mathematical Society, vol. 129 (1967), pp. 249–282.CrossRefGoogle Scholar
[Pl 1]Platek, R., A countable hierarchy for the superjump, Logic Colloquium '69 (Gandy, R. O. and Yates, C. E. M., editors), North-Holland, Amsterdam, 1971, pp. 257–271.Google Scholar
[Sh 1]Shoenfield, J., A hierarchy based on a type 2 object, Transactions of the American Mathematical Society, vol. 134 (1968), pp. 103–108.Google Scholar
[Tu 1]Tugue, T., Predicates recursive in a type 2 object and Kleene hierarchies, Commentarii Mathematici Universitatis Sancti Pauli, vol. 8 (1960), pp. 97–117.Google Scholar