Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T14:16:46.840Z Has data issue: false hasContentIssue false
  • English
  • Français

Recursion in a quantifier vs. elementary induction1

Published online by Cambridge University Press:  12 March 2014

Phokion G. Kolaitis
Phokion G. Kolaitis*
Affiliation:
University of California, Los Angeles, Los Angeles, CA 90024
Get access Rights & Permissions [Opens in a new window]

Extract

Spector [21] proved that a relation R on ω is Π11 if and only if it is (positive elementary) inductive on the structure 〈ω, +, ·〉; Kleene [8] showed that R is Π11 if and only if it is semirecursive in the type 2 object E. These two “constructive” characterizations of the Π11 relations have led to the independent study of (positive elementary) induction and recursion in E on an arbitrary structure, as natural generalizations of the theory of Π11 relations on (ω, +, · 〉.

The theory of (positive elementary) induction on an arbitrary structure was developed by Moschovakis in his book Elementary induction on abstract structures (EIAS); one of the most important theorems there is a generalization of the classical theorem of Spector [20] and Gandy [3] about the Π11 relations on ω: a relation R is inductive on an acceptable structure 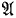. if and only if there is a formula φ(Y, x) of the language of 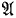such that:

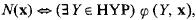
where HYP is the collection of hyperelementary relations on .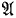

Moschovakis [17] and Kechris and Moschovakis [6] showed how to develop the theory of recursion in higher types as a chapter in the general theory of inductive definability. This approach to recursion in higher types makes it possible to use methods from the theory of inductive definability in studying recursion in E.

In this paper we establish some results about recursion in E on a structure which bolster the naturalness of this theory and contribute to its comparison with (positive elementary) induction.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 44 , Issue 2 , June 1979 , pp. 235 - 259
Copyright
Copyright © Association for Symbolic Logic 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This paper is part of the author's Ph.D. dissertation to be submitted to the University of California, Los Angeles. The author wishes to express his gratitude to his teacher and thesis advisor, Professor Yiannis N. Moschovakis, for creating his interest in inductive definability, as well as for the guidance and encouragement he received from him throughout the preparation of this paper.

References

REFERENCES

[1]Aczel, P., Representability in some systems of second order arithemtic, Israel Journal of Mathematica, vol. 8 (1970), pp. 309–328.CrossRefGoogle Scholar
[2]Aczel, P., Stage comparison theorems and game playing with inductive definitions, unpublished notes. 1972.Google Scholar
[3]Gandy, R. O., Proof of Mostowski's conjecture, Bulletin de l'Académie Polonaise des Sciences. Série des Sciences Mathématique Astronomique et Physiques, vol. 8 (1960), pp. 571–575.Google Scholar
[4]Gandy, R. O., Inductive definitions, Generalized recursion theory (Fenstad, J. E. and Hinman, P. G., Editors), North-Holland, Amsterdam, 1974, pp. 265–299.Google Scholar
[5]Hinman, P. G., Hierarchies of effective descriptive set theory, Transactions of the American Mathematical Society, vol. 142 (1969), pp. 111–140.CrossRefGoogle Scholar
[6]Kechris, A. S. and Moschovakis, Y. N., Recursion in higher types, Handbook of mathematical logic (Barwise, J., Editor), North-Holland, Amsterdam, 1977, pp. 681–737.CrossRefGoogle Scholar
[7]Kirousis, L. M., A note on recursion in E, unpublished notes, 1976.Google Scholar
[8]Kleene, S. C., Recursive functionals and quantifiers of finite type. I, Transactions of the American Mathematical Society, vol. 91 (1959), pp. 1–52.Google Scholar
[9]Kleene, S. C., Quantification of number theoretic functions, Compositio Mathematica, vol. 14 (1959), pp. 23–40.Google Scholar
[10]Kreisel, G., Set theoretic problems suggested by the notion of potential totality, Infinistic methods, Pergamon Press, New York, 1961, pp. 103–140.Google Scholar
[11]MacQueen, D. B., Post's problem for recursion in higher types, Ph.D. Thesis, Massachusetts Institute of Technology, 1972.Google Scholar
[12]Moschovakis, Y. N., Abstract first order computability. II, Transactions of the American Mathematical Society, vol. 138 (1969), pp. 464–504.Google Scholar
[13]Moschovakis, Y. N., Abstract computability and invariant definability, this Journal, vol. 34 (1969), pp. 605–633.Google Scholar
[14]Moschovakis, Y. N., The Suslin-Kleene theorem for countable structures, Duke Mathematical Journal, vol. 37 (1970), pp. 341–352.CrossRefGoogle Scholar
[15]Moschovakis, Y. N., Elementary induction on abstract structures, North-Holland, Amsterdam.Google Scholar
[16]Moschovakis, Y. N., Structural characterizations of classes of relations, Generalized recursion theory (Fenstad, J. E. and Hinman, P. G., editors), North-Holland, Amsterdam, 1974, pp. 53–79.Google Scholar
[17]Moschovakis, Y. N., On the basic notions in the theory of induction, Proceedings of the Fifth International Congress of Logic, Methodology and Philosophy of Science (to appear).Google Scholar
[18]Normann, D., Imbedding of higher type theories, Preprint Series, Oslo University, No. 16, 1974.Google Scholar
[19]Rogers, H. Jr.Theory of recursive functions and effective computability, McGraw-Hill, New York, 1967.Google Scholar
[20]Spector, C., Hyperarithemtical quantifiers, Fundamenta Mathematicae, vol. 48 (1960), pp. 313–320.CrossRefGoogle Scholar
[21]Spector, C., Inductively defined sets of natural numbers, Infinistic methods, Pergamon Press, New York, 1961, pp. 97–102.Google Scholar