Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T23:57:33.973Z Has data issue: false hasContentIssue false
  • English
  • Français

Reals n-generic relative to some perfect tree

Published online by Cambridge University Press:  12 March 2014

Bernard A. Anderson
Bernard A. Anderson*
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We say that a real X is n-generic relative to a perfect tree T if X is a path through T and for all 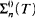sets S, there exists a number k such that either X∣k ϵ S or for all a σ ϵ T extending X∣k we have a σ ∉ S. A real X is n-generic relative to some perfect tree if there exists such a T. We first show that for every number n all but countably many reals are n-generic relative to some perfect tree. Second, we show that proving this statement requires ZFC− + “∃ infinitely many iterates of the power set of ω”. Third, we prove that every finite iterate of the hyperjump, 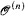, is not 2-generic relative to any perfect tree and for every ordinal α below the least λ such that supβ<λ (βth admissible) = λ, the iterated hyperjump 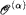is not 5-generic relative to any perfect tree. Finally, we demonstrate some necessary conditions for reals to be 1-generic relative to some perfect tree.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 2 , June 2008 , pp. 401 - 411
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Cenzer, D., Clote, P., Smith, R. L., Soare, R. I., and Wainer, S. S., Members of countable classes, Annals of Pure and Applied Logic, vol. 31 (1986), pp. 145–163.CrossRefGoogle Scholar
[2]Enderton, H. B. and Putnam, H., A note on the hyperarithmetical hierarchy, this Journal, vol. 35 (1970), pp. 429–430.Google Scholar
[3]Jockusch, C. G. Jr. and Posner, D. B., Double jumps of minimal degrees, this Journal, vol. 43 (1978), pp. 715–724.Google Scholar
[4]Jockusch, C. G. Jr. and Shore, R. A., Psuedo-jump operators II: Transfinite iterations, hierarchies, and minimal covers, this Journal, vol. 49 (1984), pp. 1205–1236.Google Scholar
[5]Kumabe, M., Degrees of generic sets, Computability, enumerability, unsolvability, London Mathematical Society, Lecture Note Series, vol. 224, Cambridge University Press, Cambridge, 1996, pp. 167–183.CrossRefGoogle Scholar
[6]Martin, D. A., Mathematical evidence, Truth in mathematics (Dales, H. G. and Oliveri, G., editors), Clarendon Press, Oxford, 1998, pp. 215–231.CrossRefGoogle Scholar
[7]Martin, D. A., Private communication, 03 2006.Google Scholar
[8]Mohrherr, J., Density of a final segment of the truth-table degrees, Pacific Journal of Mathematics, vol. 115 (1984), pp. 409–419.CrossRefGoogle Scholar
[9]Reimann, J. and Slaman, T. A., Randomness for continuous measures, To appear.Google Scholar
[10]Sacks, G. E., Higher recursion theory, Springer-Verlag, 1990.CrossRefGoogle Scholar
[11]Slaman, T. A., Private communication, 12 2004.Google Scholar
[12]Slaman, T. A., Private communication, 02 2006.Google Scholar