No CrossRef data available.
Article contents
RANK AND RANDOMNESS
Published online by Cambridge University Press: 19 September 2019
Abstract
We show that for each computable ordinal 
$\alpha > 0$ it is possible to find in each Martin-Löf random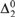 
${\rm{\Delta }}_2^0 $ degree a sequence R of Cantor-Bendixson rank α, while ensuring that the sequences that inductively witness R’s rank are all Martin-Löf random with respect to a single countably supported and computable measure. This is a strengthening for random degrees of a recent result of Downey, Wu, and Yang, and can be understood as a randomized version of it.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2019
References
REFERENCES
Ash, C. J. and Knight, J., Computable Structures and the Hyperarithmetical Hierarchy, Studies in Logic and the Foundations of Mathematics, vol. 144, North Holland, Amsterdam, 2000.Google Scholar
Bienvenu, L. and Porter, C., Strong reductions in effective randomness. Theoretical Computer Science, vol. 459 (2012), pp. 55–68.CrossRefGoogle Scholar
Binns, S., 
${\rm{\Delta }}_2^0 $ classes with complex elements , this Journal, vol. 73 (2008), no. 4, pp. 1341–1353.Google Scholar
${\rm{\Delta }}_2^0 $ classes with complex elements , this Journal, vol. 73 (2008), no. 4, pp. 1341–1353.Google ScholarCenzer, D., ${\rm{\Pi }}_1^0 $classes in computability theory, Handbook of Computability Theory (Griffor, E. R., editor), Studies in Logic and the Foundations of Mathematics, vol. 140, North Holland, Amsterdam, 1999, pp. 37–85.CrossRefGoogle Scholar
${\rm{\Pi }}_1^0 $classes in computability theory, Handbook of Computability Theory (Griffor, E. R., editor), Studies in Logic and the Foundations of Mathematics, vol. 140, North Holland, Amsterdam, 1999, pp. 37–85.CrossRefGoogle ScholarCenzer, D. and Remmel, J., Index sets for ${\rm{\Pi }}_1^0 $ classes. Annals of Pure and Applied Logic , vol. 93 (1998), no. 1–3, pp. 3–61.CrossRefGoogle Scholar
${\rm{\Pi }}_1^0 $ classes. Annals of Pure and Applied Logic , vol. 93 (1998), no. 1–3, pp. 3–61.CrossRefGoogle ScholarCenzer, D. and Smith, R. L., On the ranked points of a ${\rm{\Pi }}_1^0 $ set , this Journal, vol. 54 (1989), no. 3, pp. 975–991.Google Scholar
${\rm{\Pi }}_1^0 $ set , this Journal, vol. 54 (1989), no. 3, pp. 975–991.Google ScholarCholak, P. and Downey, R., On the Cantor-Bendixon rank of recursively enumerable sets, this Journal, vol. 58 (1993), no. 2, pp. 629–640.Google Scholar
Downey, R. G., Wu, G., and Yang, Y., The members of thin and minimal ${\rm{\Pi }}_1^0 $ classes, their ranks and Turing degrees. Annals of Pure and Applied Logic , vol. 166 (2015), no. 7–8, pp. 755–766.CrossRefGoogle Scholar
${\rm{\Pi }}_1^0 $ classes, their ranks and Turing degrees. Annals of Pure and Applied Logic , vol. 166 (2015), no. 7–8, pp. 755–766.CrossRefGoogle ScholarHölzl, R. and Porter, C. P., Randomness for computable measures and initial segment complexity. Annals of Pure and Applied Logic, vol. 168 (2017), no. 4, pp. 860–886.CrossRefGoogle Scholar
Kreisel, G., Analysis of the Cantor-Bendixson theorem by means of the analytic hierarchy. Bulletin de l’Académie Polonaise des Sciences, Série des Sciences Mathématiques, Astronomiques et Physiques, vol. 7 (1959), pp. 621–626.Google Scholar
Odifreddi, P., Classical Recursion Theory Vol. II, Studies in Logic and the Foundations of Mathematics, vol. 143, North Holland, Amsterdam, 1999.Google Scholar
Owings, J., Rank, join, and Cantor singletons. Archive for Mathematical Logic, vol. 36 (1997), no. 4–5, pp. 313–320.CrossRefGoogle Scholar
Porter, C. P., Trivial measures are not so trivial. Theory of Computing Systems, vol. 56 (2015), no. 3, pp. 487–512.CrossRefGoogle Scholar
Zvonkin, A. K. and Levin, L. A., The complexity of finite objects and the basing of the concepts of information and randomness on the theory of algorithms. Uspekhi Matematicheskikh Nauk, vol. 25 (1970), no. 6(156), pp. 85–127.Google Scholar