Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-22T20:33:00.242Z Has data issue: false hasContentIssue false
  • English
  • Français

RANDOMNESS IN THE HIGHER SETTING

Published online by Cambridge University Press:  22 December 2015

C. T. CHONG  and
LIANG YU
C. T. CHONG
Affiliation:
DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE NATIONAL UNIVERSITY OF SINGAPORE SINGAPORE 119076, SINGAPOREE-mail: [email protected]
LIANG YU
Affiliation:
INSTITUTE OF MATHEMATICAL SCIENCE NANJING UNIVERSITY, JIANGSU PROVINCE 210093 P. R. OF CHINAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the strengths of various notions of higher randomness: (i) strong 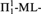${\rm{\Pi }}_1^1$randomness is separated from 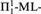${\rm{\Pi }}_1^1$randomness; (ii) the hyperdegrees of 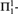${\rm{\Pi }}_1^1$random reals are closed downwards (except for the trivial degree); (iii) the reals z in 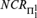$NC{R_{{\rm{\Pi }}_1^1}}$ are precisely those satisfying 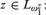$z \in {L_{\omega _1^z}}$ and (iv) lowness for 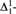${\rm{\Delta }}_1^1$randomness is strictly weaker than that for 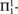${\rm{\Pi }}_1^1$randomness.

Keywords

03D3003D3268Q30Hyperarithmetic theoryhyperdegreesΠ11 randomnessΠ11 Martin-Löf randomnesslowness for higher randomness
Type
Articles
Information
The Journal of Symbolic Logic , Volume 80 , Issue 4 , December 2015 , pp. 1131 - 1148
Copyright
Copyright © The Association for Symbolic Logic 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bienvenu, Laurent, Greenberg, Noam, and Monin, Benoit, Some higher randomness results. email communication.Google Scholar
Chong, C. T., Nies, Andre, and Yu, Liang, Lowness of higher randomness notions. Israel Journal of Mathematics, vol. 166 (2008), pp. 39–60.CrossRefGoogle Scholar
Chong, C. and Yu, L., Recursion Theory. Computational Aspects of Definability, De Gruyter, Berlin, Boston, 2015.CrossRefGoogle Scholar
Demuth, Osvald, Remarks on the structure of tt-degrees based on constructive measure theory. Commentationes Mathematicae Universitatis Carolinae, vol. 29 (1988), no. 2, pp. 233–247.Google Scholar
Downey, Rod, Nies, Andre, Weber, Rebecca, and Yu, Liang, Lowness and ${\rm{\Pi }}_2^0$nullsets, this Journal, vol. 71 (2006), no. 3, pp. 1044–1052.Google Scholar
Downey, Rodney G. and Hirschfeldt, Denis R., Algorithmic randomness and complexity, Theory and Applications of Computability, Springer, New York, 2010.Google Scholar
Friedman, Harvey, One hundred and two problems in mathematical logic, this Journal, vol. 40 (1975), pp. 113–129.Google Scholar
Gandy, R. O.. On a problem of Kleene’s. Bulletin of the American Mathematical Society, vol. 66 (1960), pp. 501–502.CrossRefGoogle Scholar
Gandy, R. O., Proof of Mostowski’s conjecture. Bulletin de l’Académie Polonaise des Sciences, Série des sciences mathématiques, astronomiques et physiques, vol. 8 (1960), pp. 571–575.Google Scholar
Hjorth, Greg and Nies, André, Randomness via effective descriptive set theory. Journal of London Mathematical Society (2), vol. 75 (2007), no. 2, pp. 495–508.CrossRefGoogle Scholar
Kjos-Hanssen, Bjørn, Nies, André, Stephan, Frank, and Yu, Liang, Higher Kurtz randomness. Annals of Pure Applied Logic, vol. 161 (2010), no. 10, pp. 1280–1290.CrossRefGoogle Scholar
Martin, Donald A., Proof of a conjecture of Friedman. Proceedings of the American Mathematical Society, vol. 55 (1976), no. 1, p. 129.CrossRefGoogle Scholar
Martin-Löf, Per, On the notion of randomness. Intuitionism and Proof Theory (Proceedings of Conference at Buffalo, N.Y, 1968), pp. 73–78, North-Holland, Amsterdam, 1970.CrossRefGoogle Scholar
Monin, Benoit, Higher randomness and forcing with closed sets, 31st International Symposium on Theoretical Aspects of Computer Science, Leibniz International Proceedings in Informatics (LIPIcs), vol. 25, Schloss Dagstuhl - Leibniz-Zentrum für Informatik GmbH (LZI), Wadern, pp. 566–577.Google Scholar
Nies, André, Computability and Randomness, vol. 51, Oxford Logic Guides, Oxford University Press, Oxford, 2009.CrossRefGoogle Scholar
Reimann, Jan and Slaman, Theodore A., Measures and their random reals. Transactions of the American Mathematical Society, vol. 367 (2015), no. 7, pp. 5081–5097.CrossRefGoogle Scholar
Reimann, Jan and Slaman, Theodore A., Randomness for continuous measures, to appear.Google Scholar
Sacks, Gerald E., Measure-theoretic uniformity in recursion theory and set theory. Transactions of the American Mathematical Society, vol. 142 (1969), pp. 381–420.CrossRefGoogle Scholar
Sacks, Gerald E., Higher Recursion Theory, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1990.CrossRefGoogle Scholar
Simpson, Stephen G., Minimal covers and hyperdegrees. Transactions of the American Mathematical Society, vol. 209 (1975), pp. 45–64.CrossRefGoogle Scholar
Spector, Clifford, Hyperarithmetical quantifiers. Fundamenta Mathematicae, vol. 48 (1959/1960), pp. 313–320.CrossRefGoogle Scholar
Yu, Liang, A new proof of Friedman’s conjecture. Bulletin of Symbolic Logic, vol. 17 (2011), no. 3, pp. 455–461.CrossRefGoogle Scholar
Yu, Liang, Higher randomness, Logic Blog, http://dl.dropbox.com/u/370127/Blog/Blog2013.pdf, 2013.Google Scholar