Published online by Cambridge University Press: 22 October 2020
We describe punctual categoricity in several natural classes, including binary relational structures and mono-unary functional structures. We prove that every punctually categorical structure in a finite unary language is 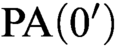 ${\text {PA}}(0')$-categorical, and we show that this upper bound is tight. We also construct an example of a punctually categorical structure whose degree of categoricity is
${\text {PA}}(0')$-categorical, and we show that this upper bound is tight. We also construct an example of a punctually categorical structure whose degree of categoricity is 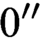 $0''$. We also prove that, with a bit of work, the latter result can be pushed beyond
$0''$. We also prove that, with a bit of work, the latter result can be pushed beyond 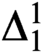 $\Delta ^1_1$, thus showing that punctually categorical structures can possess arbitrarily complex automorphism orbits.
$\Delta ^1_1$, thus showing that punctually categorical structures can possess arbitrarily complex automorphism orbits.
As a consequence, it follows that binary relational structures and unary structures are not universal with respect to primitive recursive interpretations; equivalently, in these classes every rich enough interpretation technique must necessarily involve unbounded existential quantification or infinite disjunction. In contrast, it is well-known that both classes are universal for Turing computability.
 $SPACE\left(n,\mathit{\log}(n)\right)$. this Journal, vol. 55 (1990), no. 1, pp. 260–276.Google Scholar
$SPACE\left(n,\mathit{\log}(n)\right)$. this Journal, vol. 55 (1990), no. 1, pp. 260–276.Google Scholar