Published online by Cambridge University Press: 12 March 2014
In this paper we introduce a new hierarchy of sets and operators which we call the REA hierarchy for “recursively enumerable in and above”. The hierarchy is generated by composing (possibly) transfinite sequences of the pseudo-jump operators considered in Jockusch and Shore [1983]. We there studied pseudo-jump operators defined by analogy with the Turing jump as ones taking a set A to A ⊕ 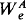 for some index e. We would now call these 1-REA operators and will extend them to α-REA operators for recursive ordinals α in analogy with the iterated Turing jump operators (A → A(α) for α <
for some index e. We would now call these 1-REA operators and will extend them to α-REA operators for recursive ordinals α in analogy with the iterated Turing jump operators (A → A(α) for α < 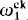 and Kleene's hyperarithmetic hierarchy. The REA sets will then, of course, be the results of applying these operators to the empty set. They will extend and generalize Kleene's H sets but will still be contained in the class of
and Kleene's hyperarithmetic hierarchy. The REA sets will then, of course, be the results of applying these operators to the empty set. They will extend and generalize Kleene's H sets but will still be contained in the class of 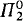 set singletons thus providing us with a new richer subclass of the
set singletons thus providing us with a new richer subclass of the 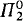 set singletons which, as we shall see, is related to the work of Harrington [1975] and [1976] on the problems of Friedman [1975] about the arithmetic degrees of such singletons. Their degrees also give a natural class extending the class H of Jockusch and McLaughlin [1969] by closing it off under transfinite iterations as well as the inclusion of [d, d′] for each degree d in the class. The reason for the class being closed under this last operation is that the REA operators include all
set singletons which, as we shall see, is related to the work of Harrington [1975] and [1976] on the problems of Friedman [1975] about the arithmetic degrees of such singletons. Their degrees also give a natural class extending the class H of Jockusch and McLaughlin [1969] by closing it off under transfinite iterations as well as the inclusion of [d, d′] for each degree d in the class. The reason for the class being closed under this last operation is that the REA operators include all 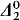 operators and so give a new hierarchy for them as well as the
operators and so give a new hierarchy for them as well as the 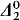 sets. This hierarchy also turns out to be related to the difference hierarchy of Ershov [1968], [1968a] and [1970]: every α-r.e. set is α-REA but each level of the REA hierarchy after the first extends all the way through the difference hierarchy although never entirely encompassing even the next level of the difference hierarchy.
sets. This hierarchy also turns out to be related to the difference hierarchy of Ershov [1968], [1968a] and [1970]: every α-r.e. set is α-REA but each level of the REA hierarchy after the first extends all the way through the difference hierarchy although never entirely encompassing even the next level of the difference hierarchy.