Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-22T21:04:51.851Z Has data issue: false hasContentIssue false
  • English
  • Français

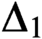PROVABLY $\Delta_1$ GAMES

Part of: Set theory

Published online by Cambridge University Press:  30 October 2020

J. P. AGUILERA  and
D. W. BLUE
J. P. AGUILERA
Affiliation:
INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY VIENNA UNIVERSITY OF TECHNOLOGY WIEDNER HAUPTSTRAßE 8-10, 1040VIENNA, AUSTRIA DEPARTMENT OF MATHEMATICS, GHENT UNIVERSITY KRIJGSLAAN 281-S8, 9000GHENT, BELGIUME-mail: [email protected]
D. W. BLUE
Affiliation:
HARVARD LOGIC CENTER, HARVARD UNIVERSITY 2 ARROW STREET, CAMBRIDGE, MA02138, USAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We isolate two abstract determinacy theorems for games of length 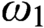$\omega_1$ from work of Neeman and use them to conclude, from large-cardinal assumptions and an iterability hypothesis in the region of measurable Woodin cardinals that

  1. (1) if the Continuum Hypothesis holds, then all games of length $\omega_1$ which are provably 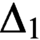$\Delta_1$ -definable from a universally Baire parameter (in first-order or $\Omega $ -logic) are determined;

  2. (2) all games of length 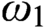$\omega_1$ with payoff constructible relative to the play are determined; and

  3. (3) if the Continuum Hypothesis holds, then there is a model of ${\mathsf{ZFC}}$ containing all reals in which all games of length 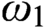$\omega_1$ definable from real and ordinal parameters are determined.

Keywords

determinacylong gamesΩ-logic

MSC classification

Primary: 03E60: Determinacy principles
Type
Articles
Information
The Journal of Symbolic Logic , Volume 85 , Issue 3 , September 2020 , pp. 1124 - 1146
Check for updates
Copyright
© The Association for Symbolic Logic 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J., Castells, N., and Larson, P., An Ω-logic primer, Set Theory (Bagaria, J. and Todorcevic, S., editors), Birkhäuser, Basel, 2006, pp. 203–242.CrossRefGoogle Scholar
Davis, M., Infinite games of perfect information , Advances in Game Theory (Dresher, M., Shapley, L. S., and Tucker, A. W., editors), Birkhäuser, Basel, 1964.Google Scholar
Feng, Q., Magidor, M., and Woodin, H., Universally Baire sets of reals , Set Theory of the Continuum (Judah, H., Just, W., and Woodin, H., editors), Springer, New York, NY, 1992, pp. 203–242.CrossRefGoogle Scholar
Kechris, A. S. and Solovay, R. M., On the relative consistency strength of determinacy hypotheses . Transactions of the American Mathematical Society , vol. 290 (1985), pp 179–211.Google Scholar
Larson, P. B., The canonical function game . Archive for Mathematical Logic , vol. 44 (2005), no. 7, pp. 817–827.CrossRefGoogle Scholar
Martin, D. A., Borel determinacy . Annals of Mathematics , vol. 102 (1975), pp. 363–371.CrossRefGoogle Scholar
Martin, D. A. and Steel, J. R., A proof of projective deterinacy . Journal of the American Mathematical Society , vol. 2 (1989), pp. 75–125.CrossRefGoogle Scholar
Moschovakis, Y. N., Descriptive Set Theory , American Mathematical Society, Providence, RI, 2009.CrossRefGoogle Scholar
Mycielski, J., On the axiom of determinacy . Fundamenta Mathematicae , vol. 53 (1964), pp. 205–224II.CrossRefGoogle Scholar
Neeman, I., Inner models in the Region of a Woodin limit of Woodin cardinals . Annals of Pure Applied Logic , vol. 116 (2002), pp. 67–155.CrossRefGoogle Scholar
Neeman, I., The Determinacy of Long Games , Walter de Gruyter, Berlin, 2004.CrossRefGoogle Scholar
Neeman, I., Games of length ω1 . Journal of Mathematical Logic , vol. 7 (2007), no. 1, pp. 83–124.CrossRefGoogle Scholar
Neeman, I. and Steel, J. R., Plus-one premice, parts I and II. Handwritten notes, 2014. 94 + 64 pp.Google Scholar
Sargsyan, G., Hod Mice and the mouse set conjecture . Memoirs of the American Mathematical Society (2014), p. 185.Google Scholar
Sargsyan, G. and Trang, N. D., The Largest Suslin Axiom, 2016. 307 pp.Google Scholar
Steel, J. R., A theorem of Woodin on mouse sets , Ordinal Definability and Recursion Theory: The Cabal Seminar, vol. III (Kechris, A. S., Löwe, B., and Steel, J. R., editors), Lecture Notes in Logic 43, Association for Symbolic Logic and Cambridge University Press, Providence, RI, 2016, pp. 243–256.CrossRefGoogle Scholar
Woodin, W. H., Supercompact cardinals, sets of reals, and weakly homogeneous trees . Proceedings of the National Academy of Sciences of the United States of America , vol. 85 (1988), p. 6587.CrossRefGoogle ScholarPubMed
Woodin, W. H., The continuum hypothesis, part II . Notices of the American Mathematical Society , vol. 48 (2001), pp. 681–690.Google Scholar
Woodin, W. H., Suitable extender models, I . Journal of Mathematical Logic , vol. 10 (2010), pp. 101–339.CrossRefGoogle Scholar
Woodin, W. H., Fine structure at the finite levels of supercompactness. Circulated manuscript, 2016. 710 pages.Google Scholar