Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-16T16:10:16.199Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of forking in ω-free pseudo-algebraically closed fields

Published online by Cambridge University Press:  12 March 2014

Zoé Chatzidakis
Zoé Chatzidakis*
Affiliation:
UFR de Mathématiques, Université Paris 7. Case 7012, 2. Place Jussieu, 75251 Paris Cedex 05, France, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

The study of pseudo-algebraically closed fields (henceforth called PAC) started with the work of J. Ax on finite and pseudo-finite fields [1]. He showed that the infinite models of the theory of finite fields are exactly the perfect PAC fields with absolute Galois group isomorphic to 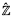, and gave elementary invariants for their first order theory, thereby proving the decidability of the theory of finite fields. Ax's results were then extended to a larger class of PAC fields by M. Jarden and U. Kiehne [21], and Jarden [19]. The final word on theories of PAC fields was given by G. Cherlin, L. van den Dries and A. Macintyre [10], see also results by Ju. Ershov [13], [14]. Let K be a PAC field. Then the elementary theory of K is entirely determined by the following data:

• The isomorphism type of the field of absolute numbers of K (the subfield of K of elements algebraic over the prime field).

• The degree of imperfection of K.

• The first-order theory, in a suitable ω-sorted language, of the inverse system of Galois groups 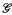al(L/K) where L runs over all finite Galois extensions of K.

They also showed that the theory of PAC fields is undecidable, by showing that any graph can be encoded in the absolute Galois group of some PAC field. It turns out that the absolute Galois group controls much of the behaviour of the PAC fields. I will give below some examples illustrating this phenomenon.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 67 , Issue 3 , September 2002 , pp. 957 - 996
Copyright
Copyright © Association for Symbolic Logic 2002

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ax, J., The elementary theory of finite fields, Annals of Mathematics, vol. 88 (1968), pp. 239–271.CrossRefGoogle Scholar
[2]Bourbaki, N., Algèbre Chapître 5, Corps commutatifs, Hermann, Paris, 1959.Google Scholar
[3]Chang, C. C. and Keisler, H. J., Model theory, North-Holland Publishing Company, Amsterdam, 1973.Google Scholar
[4]Chatzidakis, Z., Model theory of profinite groups having the Iwasawa property, Illinois Journal of Mathematics, vol. 42 (1998), no. 1, pp. 70–96.CrossRefGoogle Scholar
[5]Chatzidakis, Z., Simplicity and independence for pseudo-algebraically closed fields, Models and computability (Cooper, S. B. and Truss, J. K., editors), London Mathematical Society Lecture Notes Series, vol. 259, Cambridge University Press, Cambridge, 1999, pp. 41–61.CrossRefGoogle Scholar
[6]Chatzidakis, Z. and Pillay, A., Generic structures and simple theories, Annals of Pure and Applied Logic, vol. 95 (1998), pp. 71–92.CrossRefGoogle Scholar
[7]Chatzidakis, Z., van den Dries, L., and Macintyre, A., Definable sets over finite fields, Journal fur die reine undangewandte Mathematik, vol. 427 (1992), pp. 107–135.Google Scholar
[8]Cherlin, G. and Hrushovski, E., Smoothly approximable structures, manuscript; see also the latest version at http://www.math.rutgers.edu/~cherlin/Paper/, Pseudo-finite structures, 1994.Google Scholar
[9]Cherlin, G., van den Dries, L., and Macintyre, A., The elementary theory of regularly closed fields, preprint, 1980.Google Scholar
[10]Cherlin, G., van den Dries, L., and Macintyre, A., Decidability and undecidability theorems for PAC-fields, Bulletin of the American Mathematical Society, vol. 4 (1981), pp. 101–104.CrossRefGoogle Scholar
[11]Cherlin, G., van den Dries, L., and Macintyre, A., The elementary theory of regularly closed fields, preprint, 1982.Google Scholar
[12]Duret, J.-L., Les corps faiblement algébriquement clos non séparablement clos ont la propriété d'indépendance, Model theory of algebra and arithmetic (Pacholski, et al., editors), Lecture Notes, vol. 834, Springer-Verlag, 1980, pp. 135–157.CrossRefGoogle Scholar
[13]Ershov, Ju.L., Regularly closed fields, Soviet Math. Doklady, vol. 21 (1980), pp. 510–512.Google Scholar
[14]Ershov, Ju.L., Undecidability of regularly closed fields, Algebra and Logic, vol. 20 (1981), pp. 257–260.CrossRefGoogle Scholar
[15]Fried, M. and Jarden, M., Field arithmetic, Ergebnisse 11, Springer-Verlag, Berlin and Heidelberg, 1986.CrossRefGoogle Scholar
[16]Haran, D. and Lubotzky, A., Embedding covers and the theory of Frobenius fields, Israel Journal of Mathematics, vol. 41 (1982), pp. 181–202.CrossRefGoogle Scholar
[17]Hrushovski, E., Pseudo-finite fields and related structures, manuscript, 1991.Google Scholar
[18]Hrushovski, E. and Pillay, A., Groups definable in local fields and pseudo-finite fields, Israel Journal of Mathematics, vol. 85 (1994), pp. 203–262.CrossRefGoogle Scholar
[19]Jarden, M., The elementary theory of ω-free Ax fields, Inventiones Mathematicae, vol. 38 (1976), pp. 187–206.CrossRefGoogle Scholar
[20]Jarden, M., Algebraic dimension over Frobenius fields, Forum Mathematicum, vol. 6 (1994), pp. 43–63.CrossRefGoogle Scholar
[21]Jarden, M. and Kiehne, U., The elementary theory of algebraic fields of finite corank, Inventiones Mathematicae, vol. 30 (1975), pp. 275–294.CrossRefGoogle Scholar
[22]H., J. Keisler, Complete theories of algebraically closedfields with distinguished subfields, Michigan Mathematics Journal, vol. 11, pp. 71–81.Google Scholar
[23]Kim, B., Forking in simple unstable theories, Journal of the London Mathematical Society, vol. 57 (1998), pp. 257–267.CrossRefGoogle Scholar
[24]Kim, B., Simplicity, and stability in there, this Journal, vol. 66 (2001), no. 2, pp. 822–836.Google Scholar
[25]Kim, B. and Pillay, A., Simple theories, Annals of Pure and Applied Logic, vol. 88 (1997), no. 2-3, pp. 149–164.CrossRefGoogle Scholar
[26]Kreisel, G., and Krivine, J.-L., Eléments de logique mathématique, Dunod, Paris, 1967.Google Scholar
[27]Lang, S., Introduction to algebraic geometry, Addison-Wesley Pub. Co., Menlo Park, 1973.Google Scholar
[28]Lang, S., Fundamentals of Diophantine geometry, Springer-Verlag, New York, 1983.CrossRefGoogle Scholar
[29]Lang, S., Algebra, Addison-Wesley Pub. Co., Menlo Park, 1984.Google Scholar
[30]Mumford, D., Abelian varieties, Tata Institute of fundamental research studies in Mathematics, Oxford University Press, Bombay, 1985.Google Scholar
[31]Ribes, L., Introduction to profinite groups and Galois cohomology, Queen's papers in pure and applied mathematics, vol. 24 (1970).Google Scholar
[32]van den Dries, L., Dimension of definable sets, algebraic boundedness and henselian fields, Annals of Pure and Applied Logic, vol. 45 (1989), pp. 189–209.CrossRefGoogle Scholar