Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-19T02:49:35.126Z Has data issue: false hasContentIssue false
  • English
  • Français

A proof of Beigel's cardinality conjecture

Published online by Cambridge University Press:  12 March 2014

Martin Kummer
Martin Kummer*
Affiliation:
Institut für Logik, Komplexität und Deduktionssysteme, Universität Karlsruhe, W-7500 Karlsruhe 1, Germany, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

In 1986, Beigel [Be87] (see also [Od89, III.5.9]) proved the nonspeedup theorem: if A, B ⊆ ω, and as a function of 2n variables can be computed by an algorithm which makes at most n queries to B, then A is recursive (informally, 2n parallel queries to a nonrecursive oracle A cannot be answered by making n sequential (or “adaptive”) queries to an arbitrary oracle B). Here, 2n cannot be replaced by 2n − 1. In subsequent papers of Beigel, Gasarch, Gill, Hay, and Owings the theory of “bounded query classes” has been further developed (see, for example, [BGGOta], [BGH89], and [Ow89]). The topic has also been studied in the context of structural complexity theory (see, for example, [AG88], [Be90], and [JY90]).

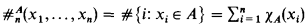If A ⊆ ω and n ≥ 1, let . Beigel [Be87] stated the powerful “cardinality conjecture” (CC): if A, B ⊆ ω, and can be computed by an algorithm which makes at most n queries to B, then A is recursive. Owings [Ow89] verified CC for n = 1, and, for n 1, he proved that A is recursive in the halting problem. We prove that CC is true for all n.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 57 , Issue 2 , June 1992 , pp. 677 - 681
Copyright
Copyright © Association for Symbolic Logic 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[AG88]Amir, A. and Gasarch, W. I., Polynomial terse sets, Information and Computation, vol. 77 (1988), pp. 37–56.CrossRefGoogle Scholar
[Be87]Beigel, R., Query-limited reducibitities, Ph.D. thesis, Department of Computer Science, Stanford University, Stanford, California, 1987.Google Scholar
[Be90]Beigel, R., Bi-immunity results for cheatable sets, Theoretical Computer Science, vol. 73 (1990), pp. 249–263.CrossRefGoogle Scholar
[BGGOta]Beigel, R., Gasarch, W. I., Gill, J. T., and Owings, J. C. Jr., Terse, superterse and verbose sets, information and Computation (to appear).Google Scholar
[BGH89]Beigel, R., Gasarch, W. I., and Hay, L., Bounded query classes and the difference hierarchy, Archive for Mathematical Logic, vol. 29 (1989), pp. 69–84.CrossRefGoogle Scholar
[D75]Deuber, W., A generalization of Ramsey's theorem for regular trees, Journal of Combinatorial Theory, ser. B, vol. 18 (1975), pp. 18–23.CrossRefGoogle Scholar
[HK092]Harizanov, V., Kummer, M., and Owings, J. C. Jr., Frequency computations and the cardinality theorem, this Journal, vol. 57 (1992), pp. 682–687.Google Scholar
[JY90]Joseph, D. and Young, P., Self-reducibility: Effects of internal structure on computational complexity, Complexity theory retrospective: in honor of Juris Hartmanis on the occasion of his sixtieth birthday (Selman, A. L., editor), Springer-Verlag, Berlin, 1990, pp. 82–107.CrossRefGoogle Scholar
[Ki72]Kinber, E. B., Frequency calculations of general recursive predicates and frequency enumeration of sets, Soviet Mathematics Doklady, vol. 13 (1972), pp. 873–876.Google Scholar
[Od89]Odifreddi, P., Classical recursion theory, North-Holland, Amsterdam, 1989.Google Scholar
[Ow89]Owings, J. C. Jr., A cardinality version of Beigel's nonspeedup theorem, this Journal, vol. 54 (1989), pp. 761–767.Google Scholar
[Tr63]Trakhtenbrot, B. A., On the frequency computability of functions, Algebra i Logika, vol. 2 (1963), pp. 25–32, (Russian)Google Scholar