Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zapletal, Jindřich
2000.
The nonstationary ideal and the other 𝜎-ideals on 𝜔₁.
Transactions of the American Mathematical Society,
Vol. 352,
Issue. 9,
p.
3981.


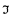 on
on 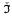 is not proper.
is not proper.