Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-22T21:03:00.807Z Has data issue: false hasContentIssue false
  • English
  • Français

Preservation theorem and relativization theorem for cofinal extensions1

Published online by Cambridge University Press:  12 March 2014

Nobuyoshi Motohashi
Nobuyoshi Motohashi*
Affiliation:
Institute of Mathematics, University of Tsukuba, Ibaraki 305, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

One of the typical preservation theorems in a first order classical predicate logic with equality L is the following theorem due to J. Łoś [4] and A. Tarski [9] (also cf. [1, p. 139]).

Theorem A (Łoś-Tarski). For any sentences A and B in L, the following two conditions (i) and (ii) are equivalent.

(i) Every extension of any model of A is a model of B.

(ii) The two sentences A ⊃ C and C ⊃ B are provable in L for some existential sentence C in L.

In [2], S. Feferman obtained a similar preservation theorem for outer extensions. In the following, we assume that L has a fixed binary predicate symbol <. Then Σ-formulas are formulas in L which are constructed from atomic formulas and their negations by applying ∧ (conjunctions), ∨ (disjunctions), ∀x < y (bounded universal quantifications), and ∃ (existential quantifications). An extension 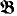of an L-structure 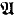is said to be an outer extension o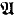f if 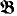⊨ a < b and b ϵ ∣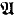∣ imply a ϵ ∣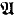∣ for any elements a, b in ∣∣.

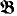Theorem B (Feferman). For any sentences A and B in L, the following two conditions (i) and (ii) are equivalent.

(i) Every outer extension of any model of A is a model of B.

(ii) The two sentences A ⊃ C and C ⊃ B are provable in L for some Σ-sentence C in L.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 51 , Issue 4 , December 1986 , pp. 1022 - 1028
Copyright
Copyright © Association for Symbolic Logic 1986

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

This paper was presented at the special session on proof theory at the January 1983 Annual Meeting of the American Mathematical Society in Denver, Colorado; unfortunately its appearance in print has been delayed until now.

References

REFERENCES

[1]Chang, C. C. and Keisler, H. J., Model theory, North-Holland, Amsterdam, 1973.Google Scholar
[2]Feferman, S., Persistent and invariant formulas for outer extensions, Compositio Mathematica, vol. 20 (1968), pp. 29–52.Google Scholar
[3]Gaifman, H., A note on models and submodels of arithmetic, Conference in mathematical logic—London '70, Lecture Notes in Mathematics, vol. 255, Springer-Verlag, Berlin, 1972, pp. 128–144.CrossRefGoogle Scholar
[4]Łoś, J., On the extending of models. I, Fundamenta Mathematicae, vol. 42 (1955), pp. 38–54.CrossRefGoogle Scholar
[5]Motohashi, N., Interpolation theorem and characterization theorem, Annals of the Japan Association for Philosophy of Science, vol. 4 (1972), pp. 85–150.CrossRefGoogle Scholar
[6]Motohashi, N., An extended relativization theorem, Journal of the Mathematical Society of Japan, vol. 25 (1973), pp. 250–256.CrossRefGoogle Scholar
[7]Motohashi, N., A normal form for first order formulas and its application to Gaifman's splitting theorem, this Journal, vol. 49 (1984), pp. 1262–1267.Google Scholar
[8]Takeuti, G., Proof theory, North-Holland, Amsterdam, 1975.Google Scholar
[9]Tarski, A., Contributions to the theory of models. I, II, Indagationes Mathematicae, vol. 16 (1954), pp. 572–581, 582–588.CrossRefGoogle Scholar