Article contents
A PREDICATIVE VARIANT OF HYLAND’S EFFECTIVE TOPOS
Published online by Cambridge University Press: 22 October 2020
Abstract
Here, we present a category 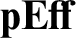 ${\mathbf {pEff}}$
which can be considered a predicative variant of Hyland's Effective Topos
${\mathbf {pEff}}$
which can be considered a predicative variant of Hyland's Effective Topos  ${{\mathbf {Eff} }}$
for the following reasons. First, its construction is carried in Feferman’s predicative theory of non-iterative fixpoints
${{\mathbf {Eff} }}$
for the following reasons. First, its construction is carried in Feferman’s predicative theory of non-iterative fixpoints 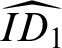 ${{\widehat {ID_1}}}$
. Second,
${{\widehat {ID_1}}}$
. Second, 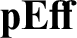 ${\mathbf {pEff}}$
is a list-arithmetic locally cartesian closed pretopos with a full subcategory
${\mathbf {pEff}}$
is a list-arithmetic locally cartesian closed pretopos with a full subcategory 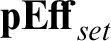 ${{\mathbf {pEff}_{set}}}$
of small objects having the same categorical structure which is preserved by the embedding in
${{\mathbf {pEff}_{set}}}$
of small objects having the same categorical structure which is preserved by the embedding in 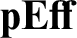 ${\mathbf {pEff}}$
; furthermore subobjects in
${\mathbf {pEff}}$
; furthermore subobjects in 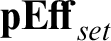 ${{\mathbf {pEff}_{set}}}$
are classified by a non-small object in
${{\mathbf {pEff}_{set}}}$
are classified by a non-small object in 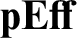 ${\mathbf {pEff}}$
. Third
${\mathbf {pEff}}$
. Third 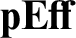 ${\mathbf {pEff}}$
happens to coincide with the exact completion of the lex category defined as a predicative rendering in
${\mathbf {pEff}}$
happens to coincide with the exact completion of the lex category defined as a predicative rendering in 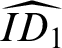 ${{\widehat {ID_1}}}$
of the subcategory of
${{\widehat {ID_1}}}$
of the subcategory of  ${{\mathbf {Eff} }}$
of recursive functions and it validates the Formal Church’s thesis. Hence pEff turns out to be itself a predicative rendering of a full subcategory of
${{\mathbf {Eff} }}$
of recursive functions and it validates the Formal Church’s thesis. Hence pEff turns out to be itself a predicative rendering of a full subcategory of  ${{\mathbf {Eff} }}$
.
${{\mathbf {Eff} }}$
.
- Type
- Article
- Information
- Copyright
- © The Association for Symbolic Logic 2020
References
- 1
- Cited by



