Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T10:40:35.284Z Has data issue: false hasContentIssue false
  • English
  • Français

Power set modulo small, the singular of uncountable cofinality

Published online by Cambridge University Press:  12 March 2014

Saharon Shelah
Saharon Shelah*
Affiliation:
The Hebrew University of Jerusalem, Einstein Institute of Mathematics, Edmond J. Safra Campus, Givat Ram Jerusalem 91904, Israel Department of Mathematics, Hill Center-Busch Campus Rutgers, The State University of New Jersey, 110 Frelinghuysen Road Piscataway, NJ 08854-8019, USA. E-mail: [email protected]: http://shelah.logic.at/
Get access Rights & Permissions [Opens in a new window]

Abstract

Let μ be singular of uncountable cofinality. If μ > 2cf(μ), we prove that in ℙ = ([μ]μ, ⊇) as a forcing notion we have a natural complete embedding of Levy(ℵ0, μ+) (so ℙ collapses μ+ to ℵ0) and even Levy (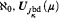). The “natural” means that the forcing ({p ∈ [μ] : p closed}, ⊇) is naturally embedded and is equivalent to the Levy algebra. Also if ℙ fails the χ-c.c. then it collapses χ to ℵ0 (and the parallel results for the case μ > ℵ0 is regular or of countable cofinality). Moreover we prove: for regular uncountable κ, there is a family P of κ partitions Ā = ⟨Aα : α < κ⟩ of κ such that for any A ∈ [κ]κ for some ⟨Aα : α < κ⟩ ∈ P we have α < κ ⇒ ∣Aα ∩ A∣ = κ.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 72 , Issue 1 , March 2007 , pp. 226 - 242
Copyright
Copyright © Association for Symbolic Logic 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[BaFr87] Balcar, Bohuslav and Franěk, František, Completion of factor algebras of ideals, Proceedings of the American Mathematical Society, vol. 100 (1987), pp. 205–212.CrossRefGoogle Scholar
[BPS] Balcar, Bohuslav, Pelant, Jan, and Simon, Petr, The space of ultrafilters on N covered by nowhere dense sets, Fundamenta Mathematical vol. CX (1980), pp. 11–24.Google Scholar
[BaSi88] Balcar, Bohuslav and Simon, Petr, On collections of almost disjoint families, Commentationes Mathematicae Universitatis Carolinae, vol. 29 (1988), pp. 631–646.Google Scholar
[BaSi89] Balcar, Bohuslav and Simon, Petr, Disjoint refinement, Handbook of boolean algebras, vol. 2, North-Holland, 1989, pp. 333–388.Google Scholar
[BaSi95] Balcar, Bohuslav and Simon, Petr, Baire number of the spaces of uniform ultrafilters, Israel Journal of Mathematics, vol. 92 (1995), pp. 263–272.CrossRefGoogle Scholar
[Ba] Baumgartner, James E., Almost disjoint sets, the dense set problem and partition calculus, Annals of Mathematical Logic, vol. 9 (1976), pp. 401–439.CrossRefGoogle Scholar
[KjSh:720] Kojman, Menachem and Shelah, Saharon, Fallen cardinals, Annals of Pure and Applied Logic, vol. 109 (2001), pp. 117–129, math.LO/0009079.CrossRefGoogle Scholar
[Sh:g] Shelah, Saharon, Cardinal arithmetic, Oxford Logic Guides, vol. 29, Oxford University Press, 1994.CrossRefGoogle Scholar
[Sh:506] Shelah, Saharon, The pcf-theorem revisited, The mathematics of Paul Erdős, II, Algorithms and Combinatorics, vol. 14, Springer, 1997, math.LO/9502233, pp. 420–459.Google Scholar
[Sh:589] Shelah, Saharon, Applications of PCF theory, this Journal, vol. 65 (2000), pp. 1624–1674.Google Scholar