Article contents
Post-scriptum à “Théories instables”
Published online by Cambridge University Press: 12 March 2014
Extract
Cette note est une suite à mon article Théories instables, this Journal, vol. 46 (1981), pp. 513–522. Quand il en a eu pris connaissance, Saharon Shelah–et c'est remplir un devoir agréable que de lui témoigner ici ma reconnaissance pour l'intérêt qu'il porte à mes travaux–m'a fait savoir qu'il pouvait en simplifier les résultats, et a publié le Théorème 1 de ce post-scriptum, pour le cas des cohéritiers, dans les “added in proof” de son Simple unstable théories, Annals of Mathematical Logic, vol. 19 (1980), pp. 177–203, plusieurs mois avant que ne paraisse l'article qu'il améliore. On verra ici que ce théorème se généralise sans problème aux fils spéciaux, et que son corollaire, le Théorème 2, représente un net progrès sur mon résultat original, puisqu'il est à la fois plus général, plus précis, et obtenu à moindre frais, le lemme sur les ultrafiltres devenant inutile.
Quelques rappels pour commencer: je considère une théorie complète T, sans propriété d'indépendance; cela signifie que toute suite … ai … indicernable dans l'ordre est insécable, c'est-à-dire qu'il ne peut exister de formule f(x, ȳ) et de paramètres 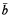 tels que f(ai,
tels que f(ai, 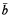 ) soit vraie cofinalement, et fausse cofinalement, dans la suite; cela signifie encore que cette suite s est découpée par la formule f(x,
) soit vraie cofinalement, et fausse cofinalement, dans la suite; cela signifie encore que cette suite s est découpée par la formule f(x, 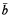 ) en un nombre fini de segments S1, …, Sk, la formule prenant la même valeur de vérité dans chaque segment, et des valeurs opposées dans des segments consécutifs; ce nombre k de segments sera appelé nombre d'alternance de la formule f(x,
) en un nombre fini de segments S1, …, Sk, la formule prenant la même valeur de vérité dans chaque segment, et des valeurs opposées dans des segments consécutifs; ce nombre k de segments sera appelé nombre d'alternance de la formule f(x, 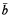 ) sur la suite s. On remarquera que, par compacité, ce nombre d'alternance est majoré en fonction seulement de f(x, ȳ).
) sur la suite s. On remarquera que, par compacité, ce nombre d'alternance est majoré en fonction seulement de f(x, ȳ).
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1983
- 2
- Cited by


