A standard enumeration of the recursively enumerable (r.e.) sets is an acceptable numbering {Wn}n∈N of the r.e. sets in the sense of Rogers [5, p. 41], together with a 1:1 recursive function f with range 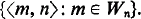In his quest for nonrecursive incomplete r.e. sets Post [4] constructed a hypersimple set Hf, relative to a fixed but unspecified standard enumeration f. Although it was later shown that hyper-simplicity does not guarantee incompleteness, the ironic possibility remained that Post's own particular hypersimple set might be incomplete. We settle the question by proving that H, may be either complete or incomplete depending upon which standard enumeration f is used. In contrast, D. A. Martin has shown [3] that Post's simple set S [4, p. 298] is complete for any standard enumeration. Furthermore, what most modern recursion theorists would regard as the “natural” construction of a hypersimple set (which we give in §1) is also complete for any standard enumeration.

There are two conclusions to be drawn from these results. First, they substantiate the often repeated remark among recursion theorists that Post's hypersimple set construction is a precursor of priority constructions because priorities play a strong role, and because there is a great deal of “restraint” which tends to keep elements out of the set. Secondly, the results warn recursion theorists that more properties than might have been supposed depend upon which standard enumeration is chosen at the beginning of the construction of some r.e. set.