Published online by Cambridge University Press: 10 June 2021
A notion of interpretation between arbitrary logics is introduced, and the poset 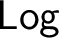 $\mathsf {Log}$
of all logics ordered under interpretability is studied. It is shown that in
$\mathsf {Log}$
of all logics ordered under interpretability is studied. It is shown that in 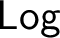 $\mathsf {Log}$
infima of arbitrarily large sets exist, but binary suprema in general do not. On the other hand, the existence of suprema of sets of equivalential logics is established. The relations between
$\mathsf {Log}$
infima of arbitrarily large sets exist, but binary suprema in general do not. On the other hand, the existence of suprema of sets of equivalential logics is established. The relations between 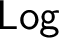 $\mathsf {Log}$
and the lattice of interpretability types of varieties are investigated.
$\mathsf {Log}$
and the lattice of interpretability types of varieties are investigated.