Article contents
Polynomially and superexponentially shorter proofs in fragments of arithmetic
Published online by Cambridge University Press: 12 March 2014
Extract
In Parikh [71] it is shown that, if T is an r.e. consistent extension of Peano arithmetic PA, then, for each primitive recursive function g, there is a formula φ of PA such that
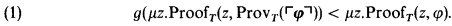
(In the following, Proof T(z, φ) and Prov T(φ) denote the metalinguistic assertions that z codes a proof of φ in T and that φ is provable in T respectively, where ProofT(z, ┌φ┐) and ProvT(┌φ┐) are the formalizations of Proof T(z,φ) and ProvT(φ) respectively in the language of PA, ┌φ┐ denotes the Gödel number of φ and ┌φ┐ denotes the corresponding numeral. Also, for typographical reasons, subscripts will not be made boldface.) If g is a rapidly increasing function, we express (1) by saying that ProvT(┌φ┐) has a much shorter proof modulo g than φ. Parikh's result is based on the fact that a suitable formula A(x), roughly asserting that (1) holds with x in place of φ, has only provable fixed points. In de Jongh and Montagna [89], this situation is generalized and investigated in a modal context. There, a characterization is given of arithmetical formulas arising from modal formulas of a suitable modal language which have only provable fixed points, and Parikh's result is obtained as a particular case.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1992
References
REFERENCES
- 3
- Cited by


