Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-22T21:44:18.302Z Has data issue: false hasContentIssue false
  • English
  • Français

The polynomial and linear hierarchies in models where the weak pigeonhole principle fails

Published online by Cambridge University Press:  12 March 2014

Leszek Aleksander Kołodziejczyk  and
Neil Thapen
Leszek Aleksander Kołodziejczyk
Affiliation:
Institute of Mathematics, University of Warsaw, Banacha 2, 02-097 Warszawa, Poland, E-mail: [email protected]
Neil Thapen
Affiliation:
Mathematical Institute, Academy of Sciences of the Czech Republic Žitná 25, CZ-115 67 Praha 1, Czech Republic, E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show, under the assumption that factoring is hard, that a model of PV exists in which the polynomial hierarchy does not collapse to the linear hierarchy; that a model of exists in which NP is not in the second level of the linear hierarchy; and that a model of exists in which the polynomial hierarchy collapses to the linear hierarchy.

Our methods are model-theoretic. We use the assumption about factoring to get a model in which the weak pigeonhole principle fails in a certain way, and then work with this failure to obtain our results.

As a corollary of one of the proofs, we also show that in the failure of WPHP (for 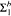definable relations) implies that the strict version of PH does not collapse to a finite level.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 73 , Issue 2 , June 2008 , pp. 578 - 592
Copyright
Copyright © Association for Symbolic Logic 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Bus86]Buss, S., Bounded arithmetic, Bibliopolis, 1986.Google Scholar
[CT06]Cook, S. and Thapen, N., The strength of replacement in weak arithmetic, ACM Transactions on Computational Logic, vol. 7 (2006), no. 4.CrossRefGoogle Scholar
[Jer07] E. Jeřábek, On independence of variants of the weak pigeonhole principle, Journal of Logic and Computation, vol. 17 (2007), no. 3, pp. 587–604.CrossRefGoogle Scholar
[Kra95] J. Krajíček, Bounded arithmetic, prepositional logic, and complexity theory, Cambridge University Press, 1995.Google Scholar
[Kra01] J. Krajíček, On the weak pigeonhole principle, Fundamenta Mathematicae, vol. 170 (2001), pp. 123–140.CrossRefGoogle Scholar
[KP98] J. Krajíček and Pudlák, P., Some consequences of cryptographical conjectures for and EF, Information and Computation, vol. 140 (1998), pp. 82–89.Google Scholar
[MPW02]Maciel, A., Pitassi, T., and Woods, A. R., A new proof of the weak pigeonhole principle, Journal of Computer and System Sciences, vol. 64 (2002), pp. 843–872.CrossRefGoogle Scholar
[PW85]Paris, J. B. and Wilkie, A. J., Counting problems in bounded arithmetic. Methods in mathematical logic, Lecture Notes in Mathematics, vol. 1130, Springer-Verlag, 1985, pp. 317–340.CrossRefGoogle Scholar
[PWW88]Paris, J. B., Wilkie, A. J., and Woods, A. R., Provability of the pigeonhole principle and the existence of infinitely many primes, this Journal, vol. 53 (1988), pp. 1235–1244.Google Scholar
[Po1OO]Pollett, C., Multifunction algebras and the provability of PH ↓, Annals of Pure and Applied Logic, vol. 104 (2000), pp. 279–303.CrossRefGoogle Scholar
[Res]Ressayre, J. P., A conservation result for systems of bounded arithmetic, unpublished manuscript, 1986.Google Scholar
[Th02]Thapen, N., A model-theoretic characterization of the weak pigeonhole principle, Annals of Pure and Applied Logic, vol. 118 (2002), pp. 175–195.CrossRefGoogle Scholar
[Th05]Thapen, N., Structures interpretable in models of bounded arithmetic. Annals of Pure and Applied Logic, vol. 136 (2005), pp. 247–266.CrossRefGoogle Scholar
[Zam96]Zambella, D., Notes on polynomially bounded arithmetic, this Journal, vol. 61 (1996), pp. 942–966.Google Scholar