Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-30T06:35:10.183Z Has data issue: false hasContentIssue false
  • English
  • Français

THE PERMUTATIONS WITH n NON-FIXED POINTS AND THE SEQUENCES WITH LENGTH n OF A SET

Part of: Set theory

Published online by Cambridge University Press:  25 July 2022

JUKKRID NUNTASRI  and
PIMPEN VEJJAJIVA
JUKKRID NUNTASRI
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE FACULTY OF SCIENCE, CHULALONGKORN UNIVERSITY BANGKOK 10330, THAILAND E-mail: [email protected]
PIMPEN VEJJAJIVA*
Affiliation:
DEPARTMENT OF MATHEMATICS AND COMPUTER SCIENCE FACULTY OF SCIENCE, CHULALONGKORN UNIVERSITY BANGKOK 10330, THAILAND E-mail: [email protected]
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We write 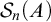$\mathcal {S}_n(A)$ for the set of permutations of a set A with n non-fixed points and 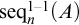$\mathrm {{seq}}^{1-1}_n(A)$ for the set of one-to-one sequences of elements of A with length n where n is a natural number greater than 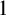$1$. With the Axiom of Choice, 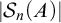$|\mathcal {S}_n(A)|$ and 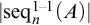$|\mathrm {{seq}}^{1-1}_n(A)|$ are equal for all infinite sets A. Among our results, we show, in ZF, that 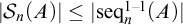$|\mathcal {S}_n(A)|\leq |\mathrm {{seq}}^{1-1}_n(A)|$ for any infinite set A if 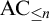${\mathrm {AC}}_{\leq n}$ is assumed and this assumption cannot be removed. In the other direction, we show that 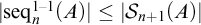$|\mathrm {{seq}}^{1-1}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A and the subscript 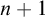$n+1$ cannot be reduced to n. Moreover, we also show that “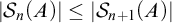$|\mathcal {S}_n(A)|\leq |\mathcal {S}_{n+1}(A)|$ for any infinite set A” is not provable in ZF.

Keywords

axiom of choicepermutationsequenceZF

MSC classification

Primary: 03E10: Ordinal and cardinal numbers
Secondary: 03E25: Axiom of choice and related propositions
Type
Article
Information
The Journal of Symbolic Logic , Volume 89 , Issue 3 , September 2024 , pp. 1067 - 1076
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Aksornthong, N. and Vejjajiva, P., Relations between cardinalities of the finite sequences and the finite subsets of a set . Mathematical Logic Quarterly , vol. 64 (2018), pp. 529–534.CrossRefGoogle Scholar
Dawson, J. Jr. and Howard, P., Factorials of infinite cardinals . Fundamenta Mathematicae , vol. 93 (1976), pp. 185–195.CrossRefGoogle Scholar
Guozhen, S., Generalizations of Cantor’s theorem in ZF . Mathematical Logic Quarterly , vol. 63 (2017), pp. 428–436.Google Scholar
Guozhen, S. and Jiachen, Y., Factorials of infinite cardinals in ZF Part I: ZF results, this Journal, vol. 85 (2020), pp. 224–243.Google Scholar
Halbeisen, L., Combinatorial Set Theory: With a Gentle Introduction to Forcing , second ed., Springer Monographs in Mathematics, Springer, Cham, 2017.CrossRefGoogle Scholar
Halbeisen, L. and Shelah, S., Consequences of arithmetic for set theory, this Journal, vol. 59 (1994), pp. 30–40.Google Scholar
Halbeisen, L. and Shelah, S., Relations between some cardinals in the absence of the axiom of choice . Bulletin of Symbolic Logic , vol. 7 (2001), pp. 237–261.CrossRefGoogle Scholar
Howard, P. and Rubin, J. E., Consequences of the Axiom of Choice , Mathematical Surveys and Monographs, vol. 59, American Mathematical Society, Providence, 1998.CrossRefGoogle Scholar
Jech, T., The Axiom of Choice , Studies in Logic and the Foundations of Mathematics, vol. 75, North-Holland, Amsterdam, 1973.Google Scholar
Nuntasri, J., Panasawatwong, S., and Vejjajiva, P., The finite subsets and the permutations with finitely many non-fixed points of a set . Mathematical Logic Quarterly , vol. 67 (2021), pp. 253–258.CrossRefGoogle Scholar
Sonpanow, N. and Vejjajiva, P., Some properties of infinite factorials . Mathematical Logic Quarterly , vol. 64 (2018), pp. 201–206.CrossRefGoogle Scholar
Sonpanow, N. and Vejjajiva, P., Factorials and the finite sequences of sets . Mathematical Logic Quarterly , vol. 65 (2019), pp. 116–120.CrossRefGoogle Scholar
Specker, E., Zur Axiomatik der Mengenlehre (Fundierungs- und Auswahlaxiom) . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik , vol. 3 (1957), pp. 173–210.CrossRefGoogle Scholar
Tachtsis, E., On the existence of permutations of infinite sets without fixed points in set theory without Choice . Acta Mathematica Hungarica , vol. 157 (2018), pp. 281–300.CrossRefGoogle Scholar