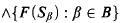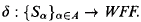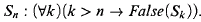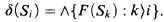Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Leitgeb, H.
2005.
Paradox by (non-wellfounded) definition.
Analysis,
Vol. 65,
Issue. 4,
p.
275.
Küdhnberger, Kai-Uwe
Löwe, Benedikt
Möllerfeld, Michael
and
Welch, Philip
2005.
Comparing Inductive and Circular Definitions: Parameters, Complexity and Games.
Studia Logica,
Vol. 81,
Issue. 1,
p.
79.
Schlenker, P.
2007.
The Elimination of Self-Reference: Generalized Yablo-Series and the Theory of Truth.
Journal of Philosophical Logic,
Vol. 36,
Issue. 3,
p.
251.
Schlenker, Philippe
2007.
How to eliminate self-reference: a précis.
Synthese,
Vol. 158,
Issue. 1,
p.
127.
Bernardi, Claudio
2009.
A Topological Approach to Yablo's Paradox.
Notre Dame Journal of Formal Logic,
Vol. 50,
Issue. 3,
Walicki, Michał
2009.
Reference, paradoxes and truth.
Synthese,
Vol. 171,
Issue. 1,
p.
195.
Cook, R. T.
2009.
Curry, Yablo and duality.
Analysis,
Vol. 69,
Issue. 4,
p.
612.
Bezem, Marc
Grabmayer, Clemens
and
Walicki, Michał
2012.
Expressive power of digraph solvability.
Annals of Pure and Applied Logic,
Vol. 163,
Issue. 3,
p.
200.
Picollo, Lavinia María
2013.
Yablo’s Paradox in Second-Order Languages: Consistency and Unsatisfiability.
Studia Logica,
Vol. 101,
Issue. 3,
p.
601.
Hsiung, Ming
2013.
Equiparadoxicality of Yablo’s Paradox and the Liar.
Journal of Logic, Language and Information,
Vol. 22,
Issue. 1,
p.
23.
Rabern, Landon
Rabern, Brian
and
Macauley, Matthew
2013.
Dangerous Reference Graphs and Semantic Paradoxes.
Journal of Philosophical Logic,
Vol. 42,
Issue. 5,
p.
727.
Dyrkolbotn, Sjur
2014.
Pristine Perspectives on Logic, Language, and Computation.
Vol. 8607,
Issue. ,
p.
69.
Dyrkolbotn, Sjur
and
Walicki, Michał
2014.
Propositional discourse logic.
Synthese,
Vol. 191,
Issue. 5,
p.
863.
Ripley, David
2015.
The Yablo Paradox: An Essay on Circularity By Roy T. Cook.
Analysis,
Vol. 75,
Issue. 3,
p.
523.
BERINGER, TIMO
and
SCHINDLER, THOMAS
2017.
A GRAPH-THEORETIC ANALYSIS OF THE SEMANTIC PARADOXES.
The Bulletin of Symbolic Logic,
Vol. 23,
Issue. 4,
p.
442.
Proietti, Carlo
Grossi, Davide
Smets, Sonja
and
Velázquez-Quesada, Fernando R.
2019.
Logic, Rationality, and Interaction.
Vol. 11813,
Issue. ,
p.
214.
ROSSI, LORENZO
2019.
A UNIFIED THEORY OF TRUTH AND PARADOX.
The Review of Symbolic Logic,
Vol. 12,
Issue. 2,
p.
209.
Vilasini, V
Nurgalieva, Nuriya
and
Rio, Lídia del
2019.
Multi-agent paradoxes beyond quantum theory.
New Journal of Physics,
Vol. 21,
Issue. 11,
p.
113028.
BARRIO, EDUARDO ALEJANDRO
PAILOS, FEDERICO
and
SZMUC, DAMIAN
2020.
A RECOVERY OPERATOR FOR NONTRANSITIVE APPROACHES.
The Review of Symbolic Logic,
Vol. 13,
Issue. 1,
p.
80.
Hsiung, Ming
2020.
What paradoxes depend on.
Synthese,
Vol. 197,
Issue. 2,
p.
887.