Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-28T14:21:16.351Z Has data issue: false hasContentIssue false
  • English
  • Français

Partial orderings of fixed finite dimension: Model companions and density1

Published online by Cambridge University Press:  12 March 2014

Alfred B. Manaster  and
Jeffrey B. Remmel
Alfred B. Manaster
Affiliation:
University of California, San Diego, La Jolla, California 92093
Jeffrey B. Remmel
Affiliation:
University of California, San Diego, La Jolla, California 92093
Get access Rights & Permissions [Opens in a new window]

Extract

The model companions of the theories of n-dimensional partial orderings and n-dimensional distributive lattices are found for each finite n. Each model companion is given as the theory of a structure which is specified. The model companions are model completions only for n = 1. The structure of the model companion of the theory of n-dimensional partial orderings is a lattice only for n = 1. Each of the model companions is seen to be finitely axiomatizable, and a set of basic formulas, each of which is existential, is specified for each model companion. Finally a topolo-gically natural notion of dense n-dimensional partial ordering is introduced and shown to have a finitely axiomatizable undecidable theory.

In this paragraph we shall define the notion of model companion (cf. [4]) and indicate the way in which we shall demonstrate that one theory is the model companion of another in this paper. For T and T* theories in a common language, T* is called a model companion of T if and only if the following two conditions are satisfied: first, Tand T* are mutually model consistent, which means that every model of either is embeddable in some model of the other; secondly, T* is model complete, which means that if and are both models of T* and is a substructure of , then 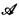is an elementary substructure of 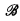. A definition of model completion may be obtained by strengthening the notion of model companion to also require that T* admit elimination of quantifiers. In all of our examples the model companion will have only one countable model. Although the ℵ0-categoricity of the model companions follows from Saracino [8], we give specific proofs since these proofs fit so naturally in our analyses.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 46 , Issue 4 , December 1981 , pp. 789 - 802
Copyright
Copyright © Association for Symbolic Logic 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

We are indebted to J. Schmerl for introducing the notion of model companion to us, providing the lemma of §3, and realizing that that lemma provides a crucial step in generalizing our results about 2-dimensional partial orderings to the results in §3.

References

REFERENCES

[1]Baker, K.A., Fishburn, P. C. and Roberts, F. S., Partial orders of dimension 2, Networks, vol. 2 (1971), pp. 11–28.CrossRefGoogle Scholar
[2]Dushnik, B. and Miller, E. W., Partially ordered sets, American Journal of Mathematics, vol. 63 (1941), pp. 600–610.CrossRefGoogle Scholar
[3]Feferman, S. and Vaught, R. L., The first order properties of algebraic systems, Fundamenta Mathematicae, vol. 47 (1959), pp. 57–103.CrossRefGoogle Scholar
[4]Macintyre, A., Model completeness, Handbook of mathematical logic (Barwise, J., Editor), North-Holland, Amsterdam, 1977, pp. 139–180.CrossRefGoogle Scholar
[5]Manaster, A. B. and Rosenstein, J. G., Two-dimensional partial orderings: undecidability, this Journal, vol. 45(1980), pp. 133–143.Google Scholar
[6]Rabin, M. O., A simple method for undecidability proofs and some applications, Logic, Methodology, and Philosophy of Science, Proceedings of the 1964 International Congress, North-Holland, Amsterdam, 1965, pp. 58–68.Google Scholar
[7]Robinson, A., Model theory as a framework for algebra, Studies in model theory (Morley, M., Editor), Mathematical Association of America, 1973, pp. 134–157.Google Scholar
[8]Saracino, D.H., Model companions for ℵ0-categorical theories, Proceedings of the American Mathematical Society, vol. 39 (1973), pp. 591–598.Google Scholar