Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-11T05:38:55.816Z Has data issue: false hasContentIssue false
  • English
  • Français

PARAMETER-FREE SCHEMES IN SECOND-ORDER ARITHMETIC

Part of: Model theory

Published online by Cambridge University Press:  27 January 2025

VICTORIA GITMAN Open the ORCID record for VICTORIA GITMAN [Opens in a new window]
VICTORIA GITMAN*
Affiliation:
THE CITY UNIVERSITY OF NEW YORK CUNY GRADUATE CENTER MATHEMATICS PROGRAM 365 FIFTH AVENUE, NEW YORK, NY 10016, USA URL: https://victoriagitman.github.io/
*
E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

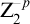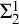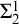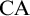Lyubetsky and Kanovei showed in [8] that there is a second-order arithmetic model of $\mathrm {Z}_2^{-p}$, (comprehension for all second-order formulas without parameters), in which $\Sigma ^1_2$-$\mathrm {CA}$ (comprehension for all $\Sigma ^1_2$-formulas with parameters) holds, but $\Sigma ^1_4$-$\mathrm {CA}$ fails. They asked whether there is a model of 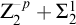$\mathrm {Z}_2^{-p}+\Sigma ^1_2$-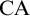$\mathrm {CA}$ with the optimal failure of 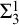$\Sigma ^1_3$-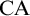$\mathrm {CA}$. We answer the question positively by constructing such a model in a forcing extension by a tree iteration of Jensen’s forcing. Let 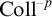$\mathrm {Coll}^{-p}$ be the parameter-free collection scheme for second-order formulas and let 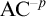$\mathrm {AC}^{-p}$ be the parameter-free choice scheme. We show that there is a model of 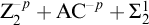$\mathrm {Z}_2^{-p}+\mathrm { AC}^{-p}+\Sigma ^1_2$-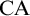$\mathrm {CA}$ with a failure of 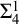$\Sigma ^1_4$-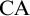$\mathrm {CA}$. We also show that there is a model of 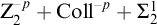$\mathrm {Z}_2^{-p}+\mathrm {Coll}^{-p}+\Sigma ^1_2$-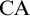$\mathrm {CA}$ with a failure of 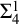$\Sigma ^1_4$-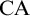$\mathrm {CA}$ and a failure of 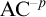$\mathrm {AC}^{-p}$, so that, in particular, the schemes 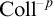$\mathrm {Coll}^{-p}$ and 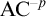$\mathrm {AC}^{-p}$ are not equivalent over $\mathrm {Z}_2^{-p}$.

Keywords

second-order arithmeticparameter-free comprehension in second-order arithmeticparameter-free choice scheme in second-order arithmetic

MSC classification

Primary: 03C62: Models of arithmetic and set theory
Type
Article
Information
The Journal of Symbolic Logic , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abraham, U., A minimal model for $\neg\mathrm{CH}$ : iteration of Jensen’s reals . Transactions of the American Mathematical Society, vol. 281 (1984), no. 2, pp. 657–674.Google Scholar
Friedman, S-D., Gitman, V., and Kanovei, V., A model of second-order arithmetic satisfying AC but not DC . Journal of Mathematical Logic, vol. 19(2019), no. 1, pp. 39, 1850013.CrossRefGoogle Scholar
Friedman, H., On the necessary use of abstract set theory . Advances in Mathematics, vol. 41 (1981), no. 3, pp. 209–280.CrossRefGoogle Scholar
Guzicki, W., On weaker forms of choice in second order arithmetic . Fundamenta Mathematicae, vol. 93 (1976), no. 2, pp. 131–144.CrossRefGoogle Scholar
Jensen, R., Definable sets of minimal degree , Mathematical Logic and Foundations of Set Theory (Proceedings of an International Colloquium Jerusalem, 1968), North-Holland, Amsterdam, 1970, pp. 122–128.Google Scholar
Kanovei, V. G. and Lyubetsky, V. A., A definable countable set containing no definable elements . Matematicheskie Zametki, vol. 102 (2017), no. 3, pp. 369–382.CrossRefGoogle Scholar
Kanovei, V. and Lyubetsky, V., On the significance of parameters in the choice and collection schemata in the 2nd order Peano arithmetic . Mathematics, vol. 11 (2023), no. 3, pp. 726.CrossRefGoogle Scholar
Kanovei, V. and Lyubetsky, V., Parameterfree comprehension does not imply full comprehension in second order Peano arithmetic . Studia Logica, (2024). https://link.springer.com/article/10.1007/s11225-024-10108-2.CrossRefGoogle Scholar
Lévy, A., Definability in axiomatic set theory. II . Mathematical Logic and Foundations of Set Theory (Proceedings of an International Colloquium Jerusalem, 1968), North-Holland, Amsterdam, 1970, pp. 129–145.Google Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, Perspectives in Logic, Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar