No CrossRef data available.
Article contents
PA RELATIVE TO AN ENUMERATION ORACLE
Published online by Cambridge University Press: 18 July 2022
Abstract
Recall that B is PA relative to A if B computes a member of every nonempty 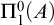 $\Pi ^0_1(A)$ class. This two-place relation is invariant under Turing equivalence and so can be thought of as a binary relation on Turing degrees. Miller and Soskova [23] introduced the notion of a
$\Pi ^0_1(A)$ class. This two-place relation is invariant under Turing equivalence and so can be thought of as a binary relation on Turing degrees. Miller and Soskova [23] introduced the notion of a 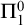 $\Pi ^0_1$ class relative to an enumeration oracle A, which they called a
$\Pi ^0_1$ class relative to an enumeration oracle A, which they called a  $\Pi ^0_1{\left \langle {A}\right \rangle }$ class. We study the induced extension of the relation B is PA relative to A to enumeration oracles and hence enumeration degrees. We isolate several classes of enumeration degrees based on their behavior with respect to this relation: the PA bounded degrees, the degrees that have a universal class, the low for PA degrees, and the
$\Pi ^0_1{\left \langle {A}\right \rangle }$ class. We study the induced extension of the relation B is PA relative to A to enumeration oracles and hence enumeration degrees. We isolate several classes of enumeration degrees based on their behavior with respect to this relation: the PA bounded degrees, the degrees that have a universal class, the low for PA degrees, and the 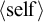 ${\left \langle {\text {self}\kern1pt}\right \rangle }$-PA degrees. We study the relationship between these classes and other known classes of enumeration degrees. We also investigate a group of classes of enumeration degrees that were introduced by Kalimullin and Puzarenko [14] based on properties that are commonly studied in descriptive set theory. As part of this investigation, we give characterizations of three of their classes in terms of a special sub-collection of relativized
${\left \langle {\text {self}\kern1pt}\right \rangle }$-PA degrees. We study the relationship between these classes and other known classes of enumeration degrees. We also investigate a group of classes of enumeration degrees that were introduced by Kalimullin and Puzarenko [14] based on properties that are commonly studied in descriptive set theory. As part of this investigation, we give characterizations of three of their classes in terms of a special sub-collection of relativized 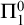 $\Pi ^0_1$ classes—the separating classes. These three can then be seen to be direct analogues of three of our classes. We completely determine the relative position of all classes in question.
$\Pi ^0_1$ classes—the separating classes. These three can then be seen to be direct analogues of three of our classes. We completely determine the relative position of all classes in question.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Association for Symbolic Logic



