Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T23:36:33.461Z Has data issue: false hasContentIssue false
  • English
  • Français

THE ORDER OF REFLECTION

Part of: Set theory Computability and recursion theory

Published online by Cambridge University Press:  08 January 2021

JUAN P. AGUILERA
JUAN P. AGUILERA*
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF GHENT KRIJGSLAAN 281-S8, 9000 GHENT, BELGIUM and INSTITUTE OF DISCRETE MATHEMATICS AND GEOMETRY VIENNA UNIVERSITY OF TECHNOLOGY WIEDNER HAUPTSTRASSE 8–10, 1040 VIENNA, AUSTRIAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

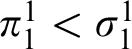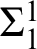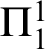Extending Aanderaa’s classical result that $\pi ^{1}_{1} < \sigma ^{1}_{1}$ , we determine the order between any two patterns of iterated $\Sigma ^{1}_{1}$ - and $\Pi ^{1}_{1}$ -reflection on ordinals. We show that this order of linear reflection is a prewellordering of length 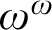$\omega ^{\omega }$ . 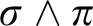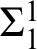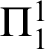This requires considering the relationship between linear and some non-linear reflection patterns, such as $\sigma \wedge \pi $ , the pattern of simultaneous $\Sigma ^{1}_{1}$ - and $\Pi ^{1}_{1}$ -reflection. The proofs involve linking the lengths of 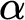$\alpha $ -recursive wellorderings to various forms of stability and reflection properties satisfied by ordinals 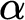$\alpha $ within standard and non-standard models of set theory.

Keywords

reflecting ordinalstabilityα-recursionGandy ordinalpattern of reflection

MSC classification

Primary: 03D60: Computability and recursion theory on ordinals, admissible sets, etc. 03E45: Inner models, including constructibility, ordinal definability, and core models
Secondary: 03D40: Word problems, etc. 03E10: Ordinal and cardinal numbers
Type
Article
Information
The Journal of Symbolic Logic , Volume 86 , Issue 4 , December 2021 , pp. 1555 - 1583
Check for updates
Copyright
© Association for Symbolic Logic 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aanderaa, S., Inductive definitions and their closure ordinals , Generalized Recursion Theory (J. E. Fenstad and P. G. Hinman, editors), North-Holland, Amsterdam, 1974, pp. 207–220.Google Scholar
Abramson, F. G. and Sacks, G. E., Uncountable Gandy ordinals . Journal of the London Mathematical Society, vol. 14 (1976), no. 2, pp. 387–392.10.1112/jlms/s2-14.3.387CrossRefGoogle Scholar
Aczel, P. and Richter, W., Inductive definitions and reflecting properties of admissible ordinals , Generalized Recursion Theory (J. E. Fenstad and P. G. Hinman, editors), 1974, pp. 301–381.10.1016/S0049-237X(08)70592-5CrossRefGoogle Scholar
Aguilera, J. P., Between the finite and the infinite, Ph.D. thesis, Vienna University of Technology, 2019.Google Scholar
Barwise, J., Admissible Sets and Structures, Perspectives of Logic, vol. 7, Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
Barwise, K. J., Gandy, R. O., and Moschovakis, Y. N., The next admissible set, this Journal, vol. 36 (1971), pp. 108–120.Google Scholar
Cenzer, D., Ordinal recursion and inductive definitions , Generalized Recursion Theory (J. E. Fenstad and P. G. Hinman, editors), 1974, pp. 221–264.10.1016/S0049-237X(08)70590-1CrossRefGoogle Scholar
Gostanian, R., The next admissible ordinal . Annals of Mathematical Logic, vol. 17 (1979), pp. 171–203.10.1016/0003-4843(79)90025-1CrossRefGoogle Scholar
Gostanian, R. and Hrbacek, K., A new proof that ${\pi}_1^1 < {\sigma}_1^1$ . Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, vol. 25 (1979), pp. 407–408.10.1002/malq.19790252504CrossRefGoogle Scholar
Rathjen, M., An ordinal analysis of parameter-free ${\varPi}_2^1$ -comprehension . Archive for Mathematical Logic, vol. 44 (2005), pp. 263–362.10.1007/s00153-004-0232-4CrossRefGoogle Scholar
Simpson, S. G., Short course on admissible recursion theory, Generalized Recursion Theory, II (J. E. Fenstad, R. O. Gandy, and G. E. Sacks, editors), North-Holland, Amsterdam, 1978, pp. 355–390.Google Scholar