Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2025-01-03T10:59:11.123Z Has data issue: false hasContentIssue false
  • English
  • Français

The optimality of induction as an axiomatization of arithmetic1

Published online by Cambridge University Press:  12 March 2014

Daniel Leivant
Daniel Leivant*
Affiliation:
Department of Computer Science, Cornell University, Ithaca, New York 14853
Get access Rights & Permissions [Opens in a new window]

Extract

By induction for a formula φ we mean the schema

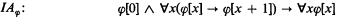
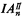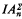(where the terms in brackets are implicitly substituted for some fixed variable, with the usual restrictions). Let be the schema IAφ for φ in Πn (i.e. ); similarly for . Each instance of 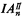is Δn+2, and each instance of 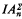is Σn+1 Thus the universal closure 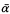of an instance α is Πn+2 in either case. Charles Parsons [72] proved that 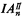and 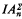are equivalent over Z0, where Z0 is essentially Primitive Recursive Arithmetic augmented by classical First Order Logic [Parsons 70].

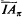Theorem. For each n > 0 there is a Πn formula π for whichis not derivable in Z0from

(i) true Πn+1sentences; nor even

(ii) Πn+1sentences consistent withZ0.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 48 , Issue 1 , March 1983 , pp. 182 - 184
Copyright
Copyright © Association for Symbolic Logic 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Research supported in part by NSF grant 78–00418.

References

REFERENCES

[Kleene 52]Kleene, S.C., Introduction to metamathematics, Noordhoff, Groningen, 1952.Google Scholar
[Kreisel 65]Kreisel, G., Mathematical logic, Lectures on Modern Mathematics, Vol. III, (Saaty, T.L., Editor), Wiley, New York, 1965, pp. 95–105.Google Scholar
[Kreisel-Wang 55]Kreisel, G. and Wang, H., Some applications of formalized consistency proofs, Fundamenta Mathematicae, vol. 42 (1955), pp. 101–110.CrossRefGoogle Scholar
[Parsons 70]Parsons, Ch., On a number theoretic choice schema and its relation to induction, Intuitionism and Proof Theory (Kino, A., Myhill, J., Vesley, R.E., Editors), North-Holland, Amsterdam, 1970, pp. 459–174.Google Scholar
[Parsons 71]Parsons, Ch., On a number theoretic choice schema II (abstract), this Journal, vol. 36 (1971), p. 578.Google Scholar
[Parsons 72]Parsons, Ch., On n-quantifier induction, this Journal, vol. 37 (1972), pp. 466–482.Google Scholar
[Smorynski 77]Smorynski, C., The incompleteness theorems, Handbook of Mathematic Logic (Barwise, J., Editor), North-Holland, Amsterdam, 1977, pp. 821–866.CrossRefGoogle Scholar