No CrossRef data available.
Article contents
ON WIDE ARONSZAJN TREES IN THE PRESENCE OF MA
Published online by Cambridge University Press: 07 September 2020
Abstract
A wide Aronszajn tree is a tree of size and height
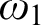 $\omega _{1}$
with no uncountable branches. We prove that under
$\omega _{1}$
with no uncountable branches. We prove that under
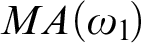 $MA(\omega _{1}\!)$
there is no wide Aronszajn tree which is universal under weak embeddings. This solves an open question of Mekler and Väänänen from 1994.
$MA(\omega _{1}\!)$
there is no wide Aronszajn tree which is universal under weak embeddings. This solves an open question of Mekler and Väänänen from 1994.
We also prove that under
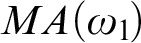 $MA(\omega _{1}\!)$
, every wide Aronszajn tree weakly embeds in an Aronszajn tree, which combined with a result of Todorčević from 2007, gives that under
$MA(\omega _{1}\!)$
, every wide Aronszajn tree weakly embeds in an Aronszajn tree, which combined with a result of Todorčević from 2007, gives that under
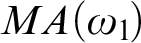 $MA(\omega _{1}\!)$
every wide Aronszajn tree embeds into a Lipschitz tree or a coherent tree. We also prove that under
$MA(\omega _{1}\!)$
every wide Aronszajn tree embeds into a Lipschitz tree or a coherent tree. We also prove that under
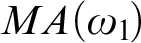 $MA(\omega _{1}\!)$
there is no wide Aronszajn tree which weakly embeds all Aronszajn trees, improving the result in the first paragraph as well as a result of Todorčević from 2007 who proved that under
$MA(\omega _{1}\!)$
there is no wide Aronszajn tree which weakly embeds all Aronszajn trees, improving the result in the first paragraph as well as a result of Todorčević from 2007 who proved that under
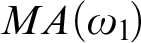 $MA(\omega _{1}\!)$
there are no universal Aronszajn trees.
$MA(\omega _{1}\!)$
there are no universal Aronszajn trees.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Association for Symbolic Logic 2020



