Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kripke, Saul A.
1965.
Formal Systems and Recursive Functions.
Vol. 40,
Issue. ,
p.
92.
1966.
Intuitionism An Introduction.
Vol. 41,
Issue. ,
p.
127.
Kreisel, G.
1970.
Intuitionism and Proof Theory: Proceedings of the Summer Conference at Buffalo N.Y. 1968.
Vol. 60,
Issue. ,
p.
121.
Troelstra, A.S.
1971.
Proceedings of the Second Scandinavian Logic Symposium.
Vol. 63,
Issue. ,
p.
369.
López-Escobar, E. G. K.
1972.
Constructions and negationless logic.
Studia Logica,
Vol. 30,
Issue. 1,
p.
7.
Lopez-Escobar, E. G. K.
and
Veldman, W.
1975.
⊨ISILC Proof Theory Symposion.
Vol. 500,
Issue. ,
p.
198.
Luckhardt, Horst
1975.
⊨ISILC Proof Theory Symposion.
Vol. 500,
Issue. ,
p.
233.
Troelstra, A.S
1977.
A note on non-extensional operations in connection with continuity and recursiveness.
Indagationes Mathematicae (Proceedings),
Vol. 80,
Issue. 5,
p.
455.
Beeson, Michael J.
1977.
Principles of continuous choice and continuity of functions in formal systems for constructive mathematics.
Annals of Mathematical Logic,
Vol. 12,
Issue. 3,
p.
249.
Troelstra, A.S.
1977.
HANDBOOK OF MATHEMATICAL LOGIC.
Vol. 90,
Issue. ,
p.
973.
Guaspari, D.
1979.
Partially conservative extensions of arithmetic.
Transactions of the American Mathematical Society,
Vol. 254,
Issue. 0,
p.
47.
Lindström, Per
1984.
On partially conservative sentences and interpretability.
Proceedings of the American Mathematical Society,
Vol. 91,
Issue. 3,
p.
436.
Leivant, Daniel
1985.
Harvey Friedman's Research on the Foundations of Mathematics.
Vol. 117,
Issue. ,
p.
231.
Nerode, Anil
1990.
Logic and Computer Science.
Vol. 1429,
Issue. ,
p.
12.
1992.
Vol. 125,
Issue. ,
p.
603.
Kurtz, Stuart A.
Mitchell, John C.
and
O'Donnell, Michael J.
1992.
Constructivity in Computer Science.
Vol. 613,
Issue. ,
p.
1.
McCarty, D. C.
1994.
On Theorems of Gödel and Kreisel: Completeness and Markov's Principle.
Notre Dame Journal of Formal Logic,
Vol. 35,
Issue. 1,
Coquand, Thierry
and
Smith, Jan M.
1996.
Types for Proofs and Programs.
Vol. 1158,
Issue. ,
p.
76.
van Oosten, Jaap
1997.
The modified realizability topos.
Journal of Pure and Applied Algebra,
Vol. 116,
Issue. 1-3,
p.
273.
Artemov, Sergei N.
2001.
Explicit Provability and Constructive Semantics.
Bulletin of Symbolic Logic,
Vol. 7,
Issue. 1,
p.
1.


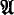 , also written as
, also written as 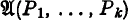 , of Heyting's predicate calculus (HPC). Then HPC is called
, of Heyting's predicate calculus (HPC). Then HPC is called 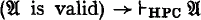 , i.e.
, i.e.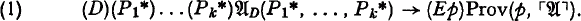
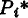 over arbitrary (possibly incompletely defined) subspecies of
over arbitrary (possibly incompletely defined) subspecies of 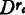 ;
;