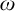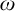1 Introduction
1.1 Motivation
Given a model-theoretic (relational) structure
![]() $\mathbb {A}$
with domain A, the set
$\mathbb {A}$
with domain A, the set
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
of all endomorphisms of
$\operatorname {\mathrm {End}}(\mathbb {A})$
of all endomorphisms of
![]() $\mathbb {A}$
is closed under composition of functions and thus forms a semigroup (even a monoid). Inheriting the subspace topology of the product topology on
$\mathbb {A}$
is closed under composition of functions and thus forms a semigroup (even a monoid). Inheriting the subspace topology of the product topology on
![]() $A^{A}$
where each copy of A is equipped with the discrete topology,
$A^{A}$
where each copy of A is equipped with the discrete topology,
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
additionally carries a topological structure which turns out to be Polish, i.e., separable and completely metrisable, in particular Hausdorff. In this topology, a sequence
$\operatorname {\mathrm {End}}(\mathbb {A})$
additionally carries a topological structure which turns out to be Polish, i.e., separable and completely metrisable, in particular Hausdorff. In this topology, a sequence
![]() $(f_{n})_{n\in \mathbb {N}}$
converges to f if and only if for every
$(f_{n})_{n\in \mathbb {N}}$
converges to f if and only if for every
![]() $a\in A$
, the sequence of evaluations
$a\in A$
, the sequence of evaluations
![]() $(f_{n}(a))_{n\in \mathbb {N}}$
converges to
$(f_{n}(a))_{n\in \mathbb {N}}$
converges to
![]() $f(a)$
in the discrete topology, i.e., if it is eventually constant with value
$f(a)$
in the discrete topology, i.e., if it is eventually constant with value
![]() $f(a)$
. For this reason, the topology is called the topology of pointwise convergence or pointwise topology for brevity. These two types of structures are compatible in the sense that the composition operation is continuous with respect to the pointwise topology; one says that the topology is a semigroup topology. For many model-theoretic structures
$f(a)$
. For this reason, the topology is called the topology of pointwise convergence or pointwise topology for brevity. These two types of structures are compatible in the sense that the composition operation is continuous with respect to the pointwise topology; one says that the topology is a semigroup topology. For many model-theoretic structures
![]() $\mathbb {A}$
on a countable domain, the algebraic (semigroup) structure and the topological (Polish) structure turn out to be so deeply intertwined that the pointwise topology is the unique Polish semigroup topology on
$\mathbb {A}$
on a countable domain, the algebraic (semigroup) structure and the topological (Polish) structure turn out to be so deeply intertwined that the pointwise topology is the unique Polish semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
. Examples include the structure without relations (whose endomorphism monoid is the full transformation monoid) [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9]; the random (di-)graph, the random strict partial order and the equivalence relation with either finitely or countably many equivalence classes of countably infinite size [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10]; as well as the rational numbers with the non-strict order [Reference Pinsker and Schindler13].
$\operatorname {\mathrm {End}}(\mathbb {A})$
. Examples include the structure without relations (whose endomorphism monoid is the full transformation monoid) [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9]; the random (di-)graph, the random strict partial order and the equivalence relation with either finitely or countably many equivalence classes of countably infinite size [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10]; as well as the rational numbers with the non-strict order [Reference Pinsker and Schindler13].
One obvious step in the proofs of these results is to show that the pointwise topology is the coarsest Polish semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
. For this purpose, the authors of [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9] transferred a notion from the theory of topological groups to the realm of semigroups, namely the so-called Zariski topology (or sometimes verbal topology) (see [Reference Bryant7, Reference Dikranjan and Toller8, Reference Markov12]); roughly speaking, the closed sets in this topology are given by solution sets to identities in the language of semigroups. Hence, the Zariski topology is an object associated with the algebraic (semi-)group structure. Considering
$\operatorname {\mathrm {End}}(\mathbb {A})$
. For this purpose, the authors of [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9] transferred a notion from the theory of topological groups to the realm of semigroups, namely the so-called Zariski topology (or sometimes verbal topology) (see [Reference Bryant7, Reference Dikranjan and Toller8, Reference Markov12]); roughly speaking, the closed sets in this topology are given by solution sets to identities in the language of semigroups. Hence, the Zariski topology is an object associated with the algebraic (semi-)group structure. Considering
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
as an abstract semigroup, the Zariski topology can thus be regarded as an “internal” object. The pointwise topology, in contrast, is defined from the evaluations at elements of the domain of
$\operatorname {\mathrm {End}}(\mathbb {A})$
as an abstract semigroup, the Zariski topology can thus be regarded as an “internal” object. The pointwise topology, in contrast, is defined from the evaluations at elements of the domain of
![]() $\mathbb {A}$
and is thus an “external” object with respect to the abstract semigroup structure of
$\mathbb {A}$
and is thus an “external” object with respect to the abstract semigroup structure of
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
—precisely speaking, the pointwise topology is associated with the semigroup action of
$\operatorname {\mathrm {End}}(\mathbb {A})$
—precisely speaking, the pointwise topology is associated with the semigroup action of
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
on A.
$\operatorname {\mathrm {End}}(\mathbb {A})$
on A.
As it turns out, the Zariski topology is necessarily coarser than any Hausdorff semigroup topology on a given semigroup. In particular, the pointwise topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
is always finer than the Zariski topology. If one manages to show that the Zariski topology on
$\operatorname {\mathrm {End}}(\mathbb {A})$
is always finer than the Zariski topology. If one manages to show that the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
even coincides with the pointwise topology for some structure
$\operatorname {\mathrm {End}}(\mathbb {A})$
even coincides with the pointwise topology for some structure
![]() $\mathbb {A}$
, one can draw two conclusions: on the one hand, the pointwise topology can also be understood as an “internal” object with respect to the abstract semigroup structure; on the other hand, the pointwise topology then indeed is the coarsest (in particular) Polish semigroup topology on
$\mathbb {A}$
, one can draw two conclusions: on the one hand, the pointwise topology can also be understood as an “internal” object with respect to the abstract semigroup structure; on the other hand, the pointwise topology then indeed is the coarsest (in particular) Polish semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
. This technique was used in [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9, Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10] as well as, implicitly, in [Reference Pinsker and Schindler13]. In each instance, however, the proof that the topologies coincide has not been particularly systematic but tuned to the specific situation being considered, based on two sets of rather technical sufficient conditions established in [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9] and the ad hoc notion of so-called arsfacere structures introduced in [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10] for which these conditions always hold. This raises the question whether there are systematic reasons for equality of the topologies, in other words general and more structural properties to require for
$\operatorname {\mathrm {End}}(\mathbb {A})$
. This technique was used in [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9, Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10] as well as, implicitly, in [Reference Pinsker and Schindler13]. In each instance, however, the proof that the topologies coincide has not been particularly systematic but tuned to the specific situation being considered, based on two sets of rather technical sufficient conditions established in [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9] and the ad hoc notion of so-called arsfacere structures introduced in [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10] for which these conditions always hold. This raises the question whether there are systematic reasons for equality of the topologies, in other words general and more structural properties to require for
![]() $\mathbb {A}$
which yield that the pointwise topology and the Zariski topology on
$\mathbb {A}$
which yield that the pointwise topology and the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincide.
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincide.
Furthermore, for each
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathbb {A}$
explicitly considered thus far, it was possible to show that the pointwise topology and the Zariski topology on
$\mathbb {A}$
explicitly considered thus far, it was possible to show that the pointwise topology and the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincide, leading to the authors of [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10] asking the following question which formed another essential motivation for the present work:
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincide, leading to the authors of [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10] asking the following question which formed another essential motivation for the present work:
Question 1.1 [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10, Question 3.1].
Is there an
![]() $\omega $
-categorical relational structure
$\omega $
-categorical relational structure
![]() $\mathbb {A}$
such that the topology of pointwise convergence on
$\mathbb {A}$
such that the topology of pointwise convergence on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
is strictly finer than the Zariski topology?
$\operatorname {\mathrm {End}}(\mathbb {A})$
is strictly finer than the Zariski topology?
1.2 Our work
We establish two new sets of sufficient conditions on a structure
![]() $\mathbb {A}$
under which the Zariski topology and the pointwise topology on
$\mathbb {A}$
under which the Zariski topology and the pointwise topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincide—so, in particular, under which the pointwise topology is the coarsest Polish (Hausdorff) semigroup topology on
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincide—so, in particular, under which the pointwise topology is the coarsest Polish (Hausdorff) semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
. To this end, we give a new application of so-called model-complete cores which have proved to be a helpful tool not only in the algebraic theory of constraint satisfaction problems [Reference Barto, Opršal and Pinsker3] but also—of independent purely mathematical interest—in the universal algebraic study of polymorphism clones of
$\operatorname {\mathrm {End}}(\mathbb {A})$
. To this end, we give a new application of so-called model-complete cores which have proved to be a helpful tool not only in the algebraic theory of constraint satisfaction problems [Reference Barto, Opršal and Pinsker3] but also—of independent purely mathematical interest—in the universal algebraic study of polymorphism clones of
![]() $\omega $
-categorical structures [Reference Barto, Kompatscher, Olšák, Van Pham and Pinsker1, Reference Barto and Pinsker4] as well as in the Ramsey-theoretic analysis of
$\omega $
-categorical structures [Reference Barto, Kompatscher, Olšák, Van Pham and Pinsker1, Reference Barto and Pinsker4] as well as in the Ramsey-theoretic analysis of
![]() $\omega $
-categorical structures [Reference Bodirsky6]. We introduce structures with mobile core—a weakening of the standard notion of transitive structures—and show that for an
$\omega $
-categorical structures [Reference Bodirsky6]. We introduce structures with mobile core—a weakening of the standard notion of transitive structures—and show that for an
![]() $\omega $
-categorical structure without algebraicity whose core is mobile such that the model-complete core of the structure is either finite or has no algebraicity itself, the Zariski topology and the pointwise topology on its endomorphism monoid coincide.
$\omega $
-categorical structure without algebraicity whose core is mobile such that the model-complete core of the structure is either finite or has no algebraicity itself, the Zariski topology and the pointwise topology on its endomorphism monoid coincide.
These two cases leave a middle ground open—namely structures whose model-complete core is infinite but has algebraicity. Thus, this is where a positive answer to Question 1.1 could be found. And indeed, we give an example of an
![]() $\omega $
-categorical structure without algebraicity whose core is mobile for which the pointwise topology on the endomorphism monoid is strictly finer than the Zariski topology. Being transitive as well as homogeneous in a finite relational language, this structure shows that even these additional standard well-behavedness assumptions are insufficient to guarantee that the two topologies coincide. This indicates that the structure of the model-complete core really contains the systematic reason for the two topologies to be equal.
$\omega $
-categorical structure without algebraicity whose core is mobile for which the pointwise topology on the endomorphism monoid is strictly finer than the Zariski topology. Being transitive as well as homogeneous in a finite relational language, this structure shows that even these additional standard well-behavedness assumptions are insufficient to guarantee that the two topologies coincide. This indicates that the structure of the model-complete core really contains the systematic reason for the two topologies to be equal.
In Section 2, we formally introduce the relevant notions, in particular the Zariski topology as well as model-complete cores. In Section 3, we prove the positive results about finite cores and cores without algebraicity stated above. Finally, Section 4 contains our counterexample.
2 Preliminaries
2.1 Structures, homomorphisms, embeddings, and automorphisms
For a function
![]() $f\colon A\to B$
between arbitrary sets
$f\colon A\to B$
between arbitrary sets
![]() $A,B$
and a tuple
$A,B$
and a tuple
![]() $\bar {a}=(a_{1},\dots ,a_{n})$
in A, we denote the tupleFootnote
1
$\bar {a}=(a_{1},\dots ,a_{n})$
in A, we denote the tupleFootnote
1
![]() $(f(a_{1}),\dots ,f(a_{n}))$
of evaluations by
$(f(a_{1}),\dots ,f(a_{n}))$
of evaluations by
![]() $f(\bar {a})$
for notational simplicity. A (relational) structure
$f(\bar {a})$
for notational simplicity. A (relational) structure
![]() $\mathbb {A}=\langle A,(R_{i})_{i\in I}\rangle $
is a domain A (in the following always finite or countably infinite) equipped with
$\mathbb {A}=\langle A,(R_{i})_{i\in I}\rangle $
is a domain A (in the following always finite or countably infinite) equipped with
![]() $m_{i}$
-ary relations
$m_{i}$
-ary relations
![]() $R_{i}\subseteq A^{m_{i}}$
. If
$R_{i}\subseteq A^{m_{i}}$
. If
![]() $\mathbb {B}=\langle B,(S_{i})_{i\in I}\rangle $
is another structure such that
$\mathbb {B}=\langle B,(S_{i})_{i\in I}\rangle $
is another structure such that
![]() $S_{i}$
also has arity
$S_{i}$
also has arity
![]() $m_{i}$
, we call a function
$m_{i}$
, we call a function
![]() $f\colon A\to B$
a homomorphism and write
$f\colon A\to B$
a homomorphism and write
![]() $f\colon \mathbb {A}\to \mathbb {B}$
if f is compatible with all
$f\colon \mathbb {A}\to \mathbb {B}$
if f is compatible with all
![]() $R_{i}$
and
$R_{i}$
and
![]() $S_{i}$
, i.e., if
$S_{i}$
, i.e., if
![]() $\bar {a}\in R_{i}$
implies
$\bar {a}\in R_{i}$
implies
![]() $f(\bar {a})\in S_{i}$
. A homomorphism
$f(\bar {a})\in S_{i}$
. A homomorphism
![]() $f\colon \mathbb {A}\to \mathbb {A}$
is called an endomorphism of
$f\colon \mathbb {A}\to \mathbb {A}$
is called an endomorphism of
![]() $\mathbb {A}$
. We denote the set of all endomorphisms of
$\mathbb {A}$
. We denote the set of all endomorphisms of
![]() $\mathbb {A}$
by
$\mathbb {A}$
by
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
; it forms a monoid with the composition operation and the neutral element
$\operatorname {\mathrm {End}}(\mathbb {A})$
; it forms a monoid with the composition operation and the neutral element
![]() $\operatorname {\mathrm {id}}_{A}$
. An embedding of
$\operatorname {\mathrm {id}}_{A}$
. An embedding of
![]() $\mathbb {A}$
into
$\mathbb {A}$
into
![]() $\mathbb {B}$
is an injective homomorphism
$\mathbb {B}$
is an injective homomorphism
![]() $f\colon \mathbb {A}\to \mathbb {B}$
which is additionally compatible with the complements of
$f\colon \mathbb {A}\to \mathbb {B}$
which is additionally compatible with the complements of
![]() $R_{i}$
and
$R_{i}$
and
![]() $S_{i}$
, equivalently if
$S_{i}$
, equivalently if
![]() $f(\bar {a})\in S_{i}$
also implies
$f(\bar {a})\in S_{i}$
also implies
![]() $\bar {a}\in R_{i}$
. The set of all self-embeddings of
$\bar {a}\in R_{i}$
. The set of all self-embeddings of
![]() $\mathbb {A}$
, i.e., of all embeddings of
$\mathbb {A}$
, i.e., of all embeddings of
![]() $\mathbb {A}$
into
$\mathbb {A}$
into
![]() $\mathbb {A}$
, is denoted by
$\mathbb {A}$
, is denoted by
![]() $\operatorname {\mathrm {Emb}}(\mathbb {A})$
; it also forms a monoid. An isomorphism between
$\operatorname {\mathrm {Emb}}(\mathbb {A})$
; it also forms a monoid. An isomorphism between
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $\mathbb {B}$
is a surjective embedding from
$\mathbb {B}$
is a surjective embedding from
![]() $\mathbb {A}$
into
$\mathbb {A}$
into
![]() $\mathbb {B}$
. The set of all automorphisms of
$\mathbb {B}$
. The set of all automorphisms of
![]() $\mathbb {A}$
, i.e., of all isomorphisms between
$\mathbb {A}$
, i.e., of all isomorphisms between
![]() $\mathbb {A}$
and itself, is denoted by
$\mathbb {A}$
and itself, is denoted by
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})$
; it forms a group with the composition operation, the neutral element
$\operatorname {\mathrm {Aut}}(\mathbb {A})$
; it forms a group with the composition operation, the neutral element
![]() $\operatorname {\mathrm {id}}_{A}$
, and the inversion operation. In the special case that
$\operatorname {\mathrm {id}}_{A}$
, and the inversion operation. In the special case that
![]() $\mathbb {A}$
is the structure without any relations, the endomorphism monoid is the full transformation monoid
$\mathbb {A}$
is the structure without any relations, the endomorphism monoid is the full transformation monoid
![]() $A^{A}$
, the self-embedding monoid is the set
$A^{A}$
, the self-embedding monoid is the set
![]() $\operatorname {\mathrm {Inj}}(A)$
of all injective maps
$\operatorname {\mathrm {Inj}}(A)$
of all injective maps
![]() $A\to A$
, and the automorphism group is the set
$A\to A$
, and the automorphism group is the set
![]() $\operatorname {\mathrm {Sym}}(A)$
of all permutations on A. A weakening of isomorphic structures is given by the following notion: Two structures
$\operatorname {\mathrm {Sym}}(A)$
of all permutations on A. A weakening of isomorphic structures is given by the following notion: Two structures
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $\mathbb {B}$
are called homomorphically equivalent if there exist homomorphisms
$\mathbb {B}$
are called homomorphically equivalent if there exist homomorphisms
![]() $g\colon \mathbb {A}\to \mathbb {B}$
and
$g\colon \mathbb {A}\to \mathbb {B}$
and
![]() $h\colon \mathbb {B}\to \mathbb {A}$
.
$h\colon \mathbb {B}\to \mathbb {A}$
.
If
![]() $C\subseteq A$
, then the induced substructure
$C\subseteq A$
, then the induced substructure
![]() $\mathbb {C}$
of
$\mathbb {C}$
of
![]() $\mathbb {A}$
on C is the structure with domain C where each relation
$\mathbb {A}$
on C is the structure with domain C where each relation
![]() $R_{i}$
is replaced by
$R_{i}$
is replaced by
![]() $R_{i}\cap C^{m_{i}}$
. If
$R_{i}\cap C^{m_{i}}$
. If
![]() $f\colon \mathbb {A}\to \mathbb {B}$
is a homomorphism, we will in a slight abuse of notation denote the substructure of
$f\colon \mathbb {A}\to \mathbb {B}$
is a homomorphism, we will in a slight abuse of notation denote the substructure of
![]() $\mathbb {B}$
on the domain
$\mathbb {B}$
on the domain
![]() $f(A)$
by
$f(A)$
by
![]() $f(\mathbb {A})$
.
$f(\mathbb {A})$
.
2.2 Topologies
If S is a semigroup, we call a topology
![]() $\mathcal {T}$
on S a semigroup topology (and
$\mathcal {T}$
on S a semigroup topology (and
![]() $(S,\mathcal {T})$
a topological semigroup) if the operation
$(S,\mathcal {T})$
a topological semigroup) if the operation
![]() $\cdot \colon S\times S\to S$
is a continuous map with respect to
$\cdot \colon S\times S\to S$
is a continuous map with respect to
![]() $\mathcal {T}$
(where
$\mathcal {T}$
(where
![]() $S\times S$
carries the product topology).
$S\times S$
carries the product topology).
A natural topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
(and also on
$\operatorname {\mathrm {End}}(\mathbb {A})$
(and also on
![]() $\operatorname {\mathrm {Emb}}(\mathbb {A}),\operatorname {\mathrm {Aut}}(\mathbb {A}),\operatorname {\mathrm {Inj}}(A),\operatorname {\mathrm {Sym}}(A)$
) is given by the subspace topology of the product topology on
$\operatorname {\mathrm {Emb}}(\mathbb {A}),\operatorname {\mathrm {Aut}}(\mathbb {A}),\operatorname {\mathrm {Inj}}(A),\operatorname {\mathrm {Sym}}(A)$
) is given by the subspace topology of the product topology on
![]() $A^{A}$
where each copy of A is equipped with the discrete topology, the so-called pointwise topology which we denote by
$A^{A}$
where each copy of A is equipped with the discrete topology, the so-called pointwise topology which we denote by
![]() $\mathcal {T}_{pw}$
(or
$\mathcal {T}_{pw}$
(or
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {A})}$
etc. if misunderstandings are possible). In the sequel, we will need to consider the topological closure of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {A})}$
etc. if misunderstandings are possible). In the sequel, we will need to consider the topological closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})$
with respect to the pointwise topology within
$\operatorname {\mathrm {Aut}}(\mathbb {A})$
with respect to the pointwise topology within
![]() $A^{A}$
(or, equivalently, within
$A^{A}$
(or, equivalently, within
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
since the latter is itself closed in
$\operatorname {\mathrm {End}}(\mathbb {A})$
since the latter is itself closed in
![]() $A^{A}$
) which we will call the
$A^{A}$
) which we will call the
![]() $\mathcal {T}_{pw}$
-closure of
$\mathcal {T}_{pw}$
-closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})$
for brevity. We remark that for an
$\operatorname {\mathrm {Aut}}(\mathbb {A})$
for brevity. We remark that for an
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathbb {A}$
, this closure consists precisely of the so-called elementary self-embeddings of
$\mathbb {A}$
, this closure consists precisely of the so-called elementary self-embeddings of
![]() $\mathbb {A}$
(see [Reference Hodges11]).
$\mathbb {A}$
(see [Reference Hodges11]).
The standard topological basis of
![]() $\mathcal {T}_{pw}$
is given by the sets
$\mathcal {T}_{pw}$
is given by the sets
It is easy to see that
![]() $\mathcal {T}_{pw}$
is a Polish semigroup topology on
$\mathcal {T}_{pw}$
is a Polish semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
.
$\operatorname {\mathrm {End}}(\mathbb {A})$
.
Now we define the Zariski topology central to this paper. For notational simplicity, we will restrict to monoids.
Definition 2.1. Let S be a monoid.
-
(i) For
 $k,\ell \in \mathbb {N}$
,
$k,\ell \in \mathbb {N}$
,
 $\ell <k$
, and for
$\ell <k$
, and for
 $p_{0},\dots ,p_{k},q_{0},\dots ,q_{\ell }\in S$
as well as
$p_{0},\dots ,p_{k},q_{0},\dots ,q_{\ell }\in S$
as well as
 $\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
$\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
 $\psi (s):=q_{\ell }sq_{\ell -1}s\dots sq_{0}$
(if
$\psi (s):=q_{\ell }sq_{\ell -1}s\dots sq_{0}$
(if
 $\ell =0$
, then
$\ell =0$
, then
 $\psi (s)=q_{0}$
for all
$\psi (s)=q_{0}$
for all
 $s\in S$
), we define
$s\in S$
), we define  $$ \begin{align*} M_{\varphi,\psi}:=\left\{s\in S:\varphi(s)\neq\psi(s)\right\}. \end{align*} $$
$$ \begin{align*} M_{\varphi,\psi}:=\left\{s\in S:\varphi(s)\neq\psi(s)\right\}. \end{align*} $$
-
(ii) The Zariski topology on S, denoted by
 $\mathcal {T}_{\text {Zariski}}$
, is the topology generated by all sets
$\mathcal {T}_{\text {Zariski}}$
, is the topology generated by all sets
 $M_{\varphi ,\psi }$
. Explicitly, the
$M_{\varphi ,\psi }$
. Explicitly, the
 $\mathcal {T}_{\text {Zariski}}$
-basic open sets are the finite intersections of sets
$\mathcal {T}_{\text {Zariski}}$
-basic open sets are the finite intersections of sets
 $M_{\varphi ,\psi }$
.
$M_{\varphi ,\psi }$
.
In general, the Zariski topology need not be a Hausdorff topology or a semigroup topology, but suitable weakenings do hold. On the one hand, it always satisfies the first separation axiom T1: every singleton set
![]() $\{s_{0}\}$
is
$\{s_{0}\}$
is
![]() $\mathcal {T}_{\text {Zariski}}$
-closed (pick
$\mathcal {T}_{\text {Zariski}}$
-closed (pick
![]() $\varphi (s)=s=1s1$
, where
$\varphi (s)=s=1s1$
, where
![]() $1$
denotes the neutral element of S, and
$1$
denotes the neutral element of S, and
![]() $\psi (s)=s_{0}$
). On the other hand, the left and right translations,
$\psi (s)=s_{0}$
). On the other hand, the left and right translations,
![]() $\lambda _{t}\colon S\to S$
,
$\lambda _{t}\colon S\to S$
,
![]() $s\mapsto ts$
and
$s\mapsto ts$
and
![]() $\rho _{t}\colon S\to S$
,
$\rho _{t}\colon S\to S$
,
![]() $s\mapsto st$
(where
$s\mapsto st$
(where
![]() $t\in S$
is fixed) are continuous with respect to the Zariski topology: To see this, take arbitrary
$t\in S$
is fixed) are continuous with respect to the Zariski topology: To see this, take arbitrary
![]() $\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
$\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
![]() $\psi (s):=q_{\ell }sq_{\ell -1}s\dots sq_{0}$
as above and note that
$\psi (s):=q_{\ell }sq_{\ell -1}s\dots sq_{0}$
as above and note that
![]() $\lambda _{t}^{-1}(M_{\varphi ,\psi })=M_{\tilde {\varphi },\tilde {\psi }}$
where
$\lambda _{t}^{-1}(M_{\varphi ,\psi })=M_{\tilde {\varphi },\tilde {\psi }}$
where
![]() $\tilde {\varphi }(s):=(p_{k}t)s(p_{k-1}t)s\dots s(p_{1}t)s(p_{0})$
and
$\tilde {\varphi }(s):=(p_{k}t)s(p_{k-1}t)s\dots s(p_{1}t)s(p_{0})$
and
![]() $\tilde {\psi }(s):=(q_{\ell }t)s(q_{\ell -1}t)s\dots s(q_{1}t)s(q_{0})$
; similarly for
$\tilde {\psi }(s):=(q_{\ell }t)s(q_{\ell -1}t)s\dots s(q_{1}t)s(q_{0})$
; similarly for
![]() $\rho _{t}$
.
$\rho _{t}$
.
By a straightforward argument, the Zariski topology is coarser than any Hausdorff semigroup topology
![]() $\mathcal {T}$
on S: One has to show that
$\mathcal {T}$
on S: One has to show that
![]() $M_{\varphi ,\psi }$
is
$M_{\varphi ,\psi }$
is
![]() $\mathcal {T}$
-open. If
$\mathcal {T}$
-open. If
![]() $s\in M_{\varphi ,\psi }$
, then
$s\in M_{\varphi ,\psi }$
, then
![]() $\varphi (s)\neq \psi (s)$
, so there exist
$\varphi (s)\neq \psi (s)$
, so there exist
![]() $U,V\in \mathcal {T}$
with
$U,V\in \mathcal {T}$
with
![]() $\varphi (s)\in U$
,
$\varphi (s)\in U$
,
![]() $\psi (s)\in V$
and
$\psi (s)\in V$
and
![]() $U\cap V=\emptyset $
since
$U\cap V=\emptyset $
since
![]() $\mathcal {T}$
is Hausdorff. Then
$\mathcal {T}$
is Hausdorff. Then
![]() $O:=\varphi ^{-1}(U)\cap \psi ^{-1}(V)$
is a
$O:=\varphi ^{-1}(U)\cap \psi ^{-1}(V)$
is a
![]() $\mathcal {T}$
-open set (by continuity of the semigroup operation) such that
$\mathcal {T}$
-open set (by continuity of the semigroup operation) such that
![]() $s\in O\subseteq M_{\varphi ,\psi }$
.
$s\in O\subseteq M_{\varphi ,\psi }$
.
2.3 Homogeneity, transitivity, and algebraicity
Several important properties of a structure
![]() $\mathbb {A}$
can be defined from the canonical group action of
$\mathbb {A}$
can be defined from the canonical group action of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})$
on
$\operatorname {\mathrm {Aut}}(\mathbb {A})$
on
![]() $A^{n}$
for
$A^{n}$
for
![]() $n\geq 1$
by evaluation which we write as
$n\geq 1$
by evaluation which we write as
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})\curvearrowright A^{n}$
. We will consider the (pointwise) stabiliser of a set
$\operatorname {\mathrm {Aut}}(\mathbb {A})\curvearrowright A^{n}$
. We will consider the (pointwise) stabiliser of a set
![]() $Y\subseteq A$
(usually finite), that is
$Y\subseteq A$
(usually finite), that is
![]() $\operatorname {\mathrm {Stab}}(Y):=\left \{\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A}):\alpha (y)=y\text { for all }y\in Y\right \}$
. For a tuple
$\operatorname {\mathrm {Stab}}(Y):=\left \{\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A}):\alpha (y)=y\text { for all }y\in Y\right \}$
. For a tuple
![]() $\bar {a}\in A^{n}$
, we further define the orbit of
$\bar {a}\in A^{n}$
, we further define the orbit of
![]() $\bar {a}$
under the action,
$\bar {a}$
under the action,
![]() $\operatorname {\mathrm {Orb}}(\bar {a}):=\left \{\alpha (\bar {a}):\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A})\right \}$
, as well as the Y-relative orbit
$\operatorname {\mathrm {Orb}}(\bar {a}):=\left \{\alpha (\bar {a}):\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A})\right \}$
, as well as the Y-relative orbit
![]() $\operatorname {\mathrm {Orb}}(\bar {a};Y):=\left \{\alpha (\bar {a}):\alpha \in \operatorname {\mathrm {Stab}}(Y)\right \}$
where
$\operatorname {\mathrm {Orb}}(\bar {a};Y):=\left \{\alpha (\bar {a}):\alpha \in \operatorname {\mathrm {Stab}}(Y)\right \}$
where
![]() $Y\subseteq A$
. By the characterisation theorem due to Engeler, Ryll-Nardzewski, and Svenonius (see [Reference Hodges11]), a countable structure
$Y\subseteq A$
. By the characterisation theorem due to Engeler, Ryll-Nardzewski, and Svenonius (see [Reference Hodges11]), a countable structure
![]() $\mathbb {A}$
is
$\mathbb {A}$
is
![]() $\omega $
-categorical if and only if for each
$\omega $
-categorical if and only if for each
![]() $n\geq 1$
, the action
$n\geq 1$
, the action
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})\curvearrowright A^{n}$
has only finitely many orbits. We say that
$\operatorname {\mathrm {Aut}}(\mathbb {A})\curvearrowright A^{n}$
has only finitely many orbits. We say that
![]() $\mathbb {A}$
is a transitive structure if the action
$\mathbb {A}$
is a transitive structure if the action
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})\curvearrowright A$
has a single orbit. The structure
$\operatorname {\mathrm {Aut}}(\mathbb {A})\curvearrowright A$
has a single orbit. The structure
![]() $\mathbb {A}$
is said to have no algebraicity if for any finite
$\mathbb {A}$
is said to have no algebraicity if for any finite
![]() $Y\subseteq A$
and any
$Y\subseteq A$
and any
![]() $a\in A\setminus Y$
, the Y-relative orbit
$a\in A\setminus Y$
, the Y-relative orbit
![]() $\operatorname {\mathrm {Orb}}(a;Y)$
is infinite. Finally, we say that
$\operatorname {\mathrm {Orb}}(a;Y)$
is infinite. Finally, we say that
![]() $\mathbb {A}$
is a homogeneous structure if any finite partial isomorphism
$\mathbb {A}$
is a homogeneous structure if any finite partial isomorphism
![]() $m\colon \bar {a}\mapsto \bar {b}$
on
$m\colon \bar {a}\mapsto \bar {b}$
on
![]() $\mathbb {A}$
can be extended to an automorphism
$\mathbb {A}$
can be extended to an automorphism
![]() $\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A})$
. It is easy to see that a homogeneous structure in a finite (relational) language, i.e.,
$\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A})$
. It is easy to see that a homogeneous structure in a finite (relational) language, i.e.,
![]() $\mathbb {A}=\langle A,(R_{i})_{i\in I}\rangle $
with I finite, is automatically
$\mathbb {A}=\langle A,(R_{i})_{i\in I}\rangle $
with I finite, is automatically
![]() $\omega $
-categorical.
$\omega $
-categorical.
In the sequel, an important property of
![]() $\omega $
-categorical structures without algebraicity will be the existence of “almost identical” embeddings/endomorphisms which can be obtained using a standard compactness argument.
$\omega $
-categorical structures without algebraicity will be the existence of “almost identical” embeddings/endomorphisms which can be obtained using a standard compactness argument.
Lemma 2.2 [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10, Lemma 3.6].
Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure without algebraicity. Then for every
$\omega $
-categorical structure without algebraicity. Then for every
![]() $a\in A$
, there are
$a\in A$
, there are
![]() $f,g$
in the
$f,g$
in the
![]() $\mathcal {T}_{pw}$
-closure of
$\mathcal {T}_{pw}$
-closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {A})$
such that
$\operatorname {\mathrm {Aut}}(\mathbb {A})$
such that
![]() $f\vert _{A\setminus \{a\}}=g\vert _{A\setminus \{a\}}$
and
$f\vert _{A\setminus \{a\}}=g\vert _{A\setminus \{a\}}$
and
![]() $f(a)\neq g(a)$
.
$f(a)\neq g(a)$
.
If f and g are as in the previous lemma, then for any
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {A})$
we note that
$s\in \operatorname {\mathrm {End}}(\mathbb {A})$
we note that
![]() $a\in \operatorname {\mathrm {Im}}(s)$
if and only if
$a\in \operatorname {\mathrm {Im}}(s)$
if and only if
![]() $\mathit{fs} \neq \mathit{gs}$
. This yields the following fact which will be at the heart of both proofs in Section 3.
$\mathit{fs} \neq \mathit{gs}$
. This yields the following fact which will be at the heart of both proofs in Section 3.
Lemma 2.3 (Contained in [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9, Proof of Lemma 5.3])
Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure without algebraicity. Then for every
$\omega $
-categorical structure without algebraicity. Then for every
![]() $a\in A$
, the set
$a\in A$
, the set
![]() $\left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):a\in \operatorname {\mathrm {Im}}(s)\right \}$
is open in the Zariski topology on
$\left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):a\in \operatorname {\mathrm {Im}}(s)\right \}$
is open in the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
.
$\operatorname {\mathrm {End}}(\mathbb {A})$
.
2.4 Cores
A structure
![]() $\mathbb {C}$
is called a model-complete core ifFootnote
2
the endomorphism monoid
$\mathbb {C}$
is called a model-complete core ifFootnote
2
the endomorphism monoid
![]() $\operatorname {\mathrm {End}}(\mathbb {C})$
coincides with the
$\operatorname {\mathrm {End}}(\mathbb {C})$
coincides with the
![]() $\mathcal {T}_{pw}$
-closure of the automorphism group
$\mathcal {T}_{pw}$
-closure of the automorphism group
![]() $\operatorname {\mathrm {Aut}}(\mathbb {C})$
. If
$\operatorname {\mathrm {Aut}}(\mathbb {C})$
. If
![]() $\mathbb {C}$
is finite, this means
$\mathbb {C}$
is finite, this means
![]() $\operatorname {\mathrm {End}}(\mathbb {C})=\operatorname {\mathrm {Aut}}(\mathbb {C})$
. Every
$\operatorname {\mathrm {End}}(\mathbb {C})=\operatorname {\mathrm {Aut}}(\mathbb {C})$
. Every
![]() $\omega $
-categorical structure has a homomorphically equivalent model-complete core structure:
$\omega $
-categorical structure has a homomorphically equivalent model-complete core structure:
Theorem 2.4 (Originally [Reference Bodirsky5, Theorem 16], alternative proof in [Reference Barto, Kompatscher, Olšák, Van Pham and Pinsker2, Theorem 5.7]).
Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure. Then there exists a model-complete core
$\omega $
-categorical structure. Then there exists a model-complete core
![]() $\mathbb {C}$
such that
$\mathbb {C}$
such that
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $\mathbb {C}$
are homomorphically equivalent. Moreover,
$\mathbb {C}$
are homomorphically equivalent. Moreover,
![]() $\mathbb {C}$
is either
$\mathbb {C}$
is either
![]() $\omega $
-categorical or finite and uniquely determined (up to isomorphism).
$\omega $
-categorical or finite and uniquely determined (up to isomorphism).
Because of the uniqueness result,
![]() $\mathbb {C}$
is commonly referred to as the model-complete core of
$\mathbb {C}$
is commonly referred to as the model-complete core of
![]() $\mathbb {A}$
. We will repeatedly use the following simple property of model-complete cores:
$\mathbb {A}$
. We will repeatedly use the following simple property of model-complete cores:
Lemma 2.5. Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure and let
$\omega $
-categorical structure and let
![]() $\mathbb {C}$
be its model-complete core. Then any homomorphism
$\mathbb {C}$
be its model-complete core. Then any homomorphism
![]() $f\colon \mathbb {C}\to \mathbb {A}$
is an embedding.
$f\colon \mathbb {C}\to \mathbb {A}$
is an embedding.
Proof If
![]() $g\colon \mathbb {A}\to \mathbb {C}$
denotes the homomorphism existing by homomorphic equivalence, then
$g\colon \mathbb {A}\to \mathbb {C}$
denotes the homomorphism existing by homomorphic equivalence, then
![]() $gf$
is an endomorphism of
$gf$
is an endomorphism of
![]() $\mathbb {C}$
and thus contained in the
$\mathbb {C}$
and thus contained in the
![]() $\mathcal {T}_{pw}$
-closure of
$\mathcal {T}_{pw}$
-closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {C})$
, in particular a self-embedding. This is only possible if f is an embedding.
$\operatorname {\mathrm {Aut}}(\mathbb {C})$
, in particular a self-embedding. This is only possible if f is an embedding.
This lemma in particular applies to the homomorphism
![]() $h\colon \mathbb {C}\to \mathbb {A}$
yielded by homomorphic equivalence. Replacing
$h\colon \mathbb {C}\to \mathbb {A}$
yielded by homomorphic equivalence. Replacing
![]() $\mathbb {C}$
by its isomorphic copy
$\mathbb {C}$
by its isomorphic copy
![]() $h(\mathbb {C})$
, we will subsequently assume that
$h(\mathbb {C})$
, we will subsequently assume that
![]() $\mathbb {C}$
is a substructure of
$\mathbb {C}$
is a substructure of
![]() $\mathbb {A}$
. Note that depending on the structure
$\mathbb {A}$
. Note that depending on the structure
![]() $\mathbb {A}$
, it can but need not be possible to pick the homomorphism
$\mathbb {A}$
, it can but need not be possible to pick the homomorphism
![]() $g\colon \mathbb {A}\to \mathbb {C}$
to be surjective. For instance, the model-complete core of the random graph is the complete graph on countably many vertices, and any bijection from the random graph to the complete graph is a surjective homomorphism.
$g\colon \mathbb {A}\to \mathbb {C}$
to be surjective. For instance, the model-complete core of the random graph is the complete graph on countably many vertices, and any bijection from the random graph to the complete graph is a surjective homomorphism.
On the other hand, if
![]() $\mathbb {A}$
is given by the rational numbers
$\mathbb {A}$
is given by the rational numbers
![]() $\mathbb {Q}$
extended by two elements
$\mathbb {Q}$
extended by two elements
![]() $\pm \infty $
, equipped with the canonical strict order, then the model-complete core of
$\pm \infty $
, equipped with the canonical strict order, then the model-complete core of
![]() $\mathbb {A}$
is precisely
$\mathbb {A}$
is precisely
![]() $\langle \mathbb {Q},<\rangle $
which cannot coincide with any homomorphic image of
$\langle \mathbb {Q},<\rangle $
which cannot coincide with any homomorphic image of
![]() $\mathbb {A}$
since such an image would have a greatest and a least element. If the model-complete core of
$\mathbb {A}$
since such an image would have a greatest and a least element. If the model-complete core of
![]() $\mathbb {A}$
is finite, however, any homomorphism
$\mathbb {A}$
is finite, however, any homomorphism
![]() $g\colon \mathbb {A}\to \mathbb {C}$
is surjective, as can be seen by viewing g as an endomorphism of
$g\colon \mathbb {A}\to \mathbb {C}$
is surjective, as can be seen by viewing g as an endomorphism of
![]() $\mathbb {A}$
and applying the following lemma we will also use later on:
$\mathbb {A}$
and applying the following lemma we will also use later on:
Lemma 2.6. If the model-complete core of an
![]() $\omega $
-categorical structure
$\omega $
-categorical structure
![]() $\mathbb {A}$
is finite of size n, then the image of any endomorphism of
$\mathbb {A}$
is finite of size n, then the image of any endomorphism of
![]() $\mathbb {A}$
has size at least n.
$\mathbb {A}$
has size at least n.
Proof If
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {A})$
, then
$s\in \operatorname {\mathrm {End}}(\mathbb {A})$
, then
![]() $s(\mathbb {A})$
is homomorphically equivalent to
$s(\mathbb {A})$
is homomorphically equivalent to
![]() $\mathbb {A}$
. Hence,
$\mathbb {A}$
. Hence,
![]() $s(\mathbb {A})$
and
$s(\mathbb {A})$
and
![]() $\mathbb {A}$
have the same model-complete core which can therefore be regarded as a substructure of
$\mathbb {A}$
have the same model-complete core which can therefore be regarded as a substructure of
![]() $s(\mathbb {A})$
.
$s(\mathbb {A})$
.
3 Two sets of sufficient conditions
This section is devoted to stating and showing our sufficient conditions, expressed in terms of the model-complete core, for the pointwise topology and the Zariski topology to coincide (see Theorem 3.2).
3.1 Our results
An essential notion for our results is given by structures with mobile core:
Definition 3.1. Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure. Then
$\omega $
-categorical structure. Then
![]() $\mathbb {A}$
is said to have a mobile core if any element of
$\mathbb {A}$
is said to have a mobile core if any element of
![]() $\mathbb {A}$
is contained in the image of an endomorphism into the model-complete core. Explicitly, for any
$\mathbb {A}$
is contained in the image of an endomorphism into the model-complete core. Explicitly, for any
![]() $a\in \mathbb {A}$
, there ought to exist a substructure
$a\in \mathbb {A}$
, there ought to exist a substructure
![]() $\mathbb {C}$
of
$\mathbb {C}$
of
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $g\in \operatorname {\mathrm {End}}(\mathbb {A})$
with the following properties:
$g\in \operatorname {\mathrm {End}}(\mathbb {A})$
with the following properties:
-
(i)
 $\mathbb {C}$
is a model-complete core homomorphically equivalent to
$\mathbb {C}$
is a model-complete core homomorphically equivalent to
 $\mathbb {A}$
.
$\mathbb {A}$
. -
(ii)
 $a\in g(A)\subseteq C$
.
$a\in g(A)\subseteq C$
.
Note that structures with mobile core are a weakening of transitive structures (as introduced in Section 2.3): Let
![]() $\mathbb {A}$
be transitive, let
$\mathbb {A}$
be transitive, let
![]() $\mathbb {C}$
be its model-complete core with homomorphism
$\mathbb {C}$
be its model-complete core with homomorphism
![]() $g\colon \mathbb {A}\to \mathbb {C}$
, and let
$g\colon \mathbb {A}\to \mathbb {C}$
, and let
![]() $a_{0}\in A$
be a fixed element. If
$a_{0}\in A$
be a fixed element. If
![]() $a\in A$
is arbitrary, then transitivity yields
$a\in A$
is arbitrary, then transitivity yields
![]() $\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A})$
such that
$\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {A})$
such that
![]() $\alpha (g(a_{0}))=a$
. Hence,
$\alpha (g(a_{0}))=a$
. Hence,
![]() $\widetilde {\mathbb {C}}:=\alpha (\mathbb {C})$
is an isomorphic copy of
$\widetilde {\mathbb {C}}:=\alpha (\mathbb {C})$
is an isomorphic copy of
![]() $\mathbb {C}$
with homomorphism
$\mathbb {C}$
with homomorphism
![]() $\tilde {g}:=\alpha g\colon \mathbb {A}\to \widetilde {\mathbb {C}}$
such that
$\tilde {g}:=\alpha g\colon \mathbb {A}\to \widetilde {\mathbb {C}}$
such that
![]() $a\in \tilde {g}(A)\subseteq \widetilde {C}$
. In fact, it suffices to assume that
$a\in \tilde {g}(A)\subseteq \widetilde {C}$
. In fact, it suffices to assume that
![]() $\mathbb {A}$
is weakly transitive, i.e., that for all
$\mathbb {A}$
is weakly transitive, i.e., that for all
![]() $a,b\in A$
there exists
$a,b\in A$
there exists
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {A})$
with
$s\in \operatorname {\mathrm {End}}(\mathbb {A})$
with
![]() $s(a)=b$
—replacing
$s(a)=b$
—replacing
![]() $\alpha $
in the above argument by s, we still obtain that
$\alpha $
in the above argument by s, we still obtain that
![]() $s(\mathbb {C})$
is an isomorphic copy of
$s(\mathbb {C})$
is an isomorphic copy of
![]() $\mathbb {C}$
by Lemma 2.5.
$\mathbb {C}$
by Lemma 2.5.
On the other hand, there exist non-transitive structures which have a mobile core, for instance the disjoint union of two transitive structures where each part gets named by an additional unary predicate (to ascertain that the parts are invariant under any automorphism). Finally, the structure
![]() $\langle \mathbb {Q}\cup \{\pm \infty \},<\rangle $
mentioned after Lemma 2.5 does not have a mobile core: The element
$\langle \mathbb {Q}\cup \{\pm \infty \},<\rangle $
mentioned after Lemma 2.5 does not have a mobile core: The element
![]() $+\infty $
cannot be contained in any copy of the model-complete core
$+\infty $
cannot be contained in any copy of the model-complete core
![]() $\langle \mathbb {Q},<\rangle $
.
$\langle \mathbb {Q},<\rangle $
.
Now we can formally state the main result of this section.
Theorem 3.2. Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure without algebraicity which has a mobile core. Then the Zariski topology on
$\omega $
-categorical structure without algebraicity which has a mobile core. Then the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincides with the pointwise topology if one of the following two conditions holds:
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincides with the pointwise topology if one of the following two conditions holds:
-
(i) EITHER the model-complete core of
 $\mathbb {A}$
is finite,
$\mathbb {A}$
is finite, -
(ii) OR the model-complete core of
 $\mathbb {A}$
is infinite and does not have algebraicity.
$\mathbb {A}$
is infinite and does not have algebraicity.
The cases (i) and (ii) will be treated separately in Sections 3.2 and 3.3, respectively. Before we get to the proofs, we show how Theorem 3.2 can be used to easily verify that the Zariski topology and the pointwise topology coincide on the endomorphism monoids of a multitude of example structures. Some of them have been treated in [Reference Elliott, Jonušas, Mitchell, Péresse and Pinsker10], but our result applies to many other structures which have not yet been considered, e.g., the random reflexive or irreflexive n-clique-free graph.
Corollary 3.3. Let
![]() $\mathbb {A}$
be one of the following structures:
$\mathbb {A}$
be one of the following structures:
-
(i)
 $\langle \mathbb {Q},\leq \rangle $
;
$\langle \mathbb {Q},\leq \rangle $
; -
(ii) the random reflexive partial order;
-
(iii) the equivalence relation with either finitely or countably many equivalence classes of countable size (for the case of a single class, this includes the complete reflexive graph on countably many vertices);
-
(iv) the random reflexive (di-)graph;
-
(v) the random reflexive n-clique-free graph;
-
(vi)
 $\langle \mathbb {Q},<\rangle $
;
$\langle \mathbb {Q},<\rangle $
; -
(vii) the random strict partial order;
-
(viii) the random tournament;
-
(ix) the irreflexive equivalence relation with either finitely or countably many equivalence classes of countable size (for the case of a single class, this includes the complete irreflexive graph on countably many vertices);
-
(x) the random irreflexive (di-)graph;
-
(xi) the random irreflexive n-clique-free graph.
Then the pointwise topology and the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincide. In particular, the pointwise topology is the coarsest Hausdorff semigroup topology on
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincide. In particular, the pointwise topology is the coarsest Hausdorff semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
.
$\operatorname {\mathrm {End}}(\mathbb {A})$
.
Proof It is immediate that all structures in (i)–(xi) are
![]() $\omega $
-categorical structures without algebraicity which are transitive (in particular, they have a mobile core). For (i)–(v), the model-complete core of
$\omega $
-categorical structures without algebraicity which are transitive (in particular, they have a mobile core). For (i)–(v), the model-complete core of
![]() $\mathbb {A}$
is merely a single point with a loop; in particular, the model-complete core is finite. For (vi) and (xi), the structure
$\mathbb {A}$
is merely a single point with a loop; in particular, the model-complete core is finite. For (vi) and (xi), the structure
![]() $\mathbb {A}$
is already a model-complete core, so the model-complete core of
$\mathbb {A}$
is already a model-complete core, so the model-complete core of
![]() $\mathbb {A}$
is just
$\mathbb {A}$
is just
![]() $\mathbb {A}$
itself. For (vii) and (viii), the model-complete core of
$\mathbb {A}$
itself. For (vii) and (viii), the model-complete core of
![]() $\mathbb {A}$
is the structure
$\mathbb {A}$
is the structure
![]() $\langle \mathbb {Q},<\rangle $
. For (ix) and (x), the model-complete core of
$\langle \mathbb {Q},<\rangle $
. For (ix) and (x), the model-complete core of
![]() $\mathbb {A}$
is the complete graph on countably infinitely vertices. Summarising, the model-complete core of
$\mathbb {A}$
is the complete graph on countably infinitely vertices. Summarising, the model-complete core of
![]() $\mathbb {A}$
has no algebraicity in (vi)–(xi).
$\mathbb {A}$
has no algebraicity in (vi)–(xi).
In any case, Theorem 3.2 applies and yields the desired conclusion.
3.2 Finite cores
First, we consider the case that
![]() $\mathbb {A}$
has a finite model-complete core.
$\mathbb {A}$
has a finite model-complete core.
Proposition 3.4. Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure without algebraicity which has a mobile core. If the model-complete core of
$\omega $
-categorical structure without algebraicity which has a mobile core. If the model-complete core of
![]() $\mathbb {A}$
is finite, then the Zariski topology on
$\mathbb {A}$
is finite, then the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincides with the pointwise topology.
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincides with the pointwise topology.
Proof We show that the
![]() $\mathcal {T}_{pw}$
-generating sets
$\mathcal {T}_{pw}$
-generating sets
![]() $\left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):s(a)=b\right \}$
,
$\left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):s(a)=b\right \}$
,
![]() $a,b\in A$
, are
$a,b\in A$
, are
![]() $\mathcal {T}_{\text {Zariski}}$
-open by proving that they are
$\mathcal {T}_{\text {Zariski}}$
-open by proving that they are
![]() $\mathcal {T}_{\text {Zariski}}$
-neighbourhoods of each element.
$\mathcal {T}_{\text {Zariski}}$
-neighbourhoods of each element.
Let
![]() $s_{0}\in \operatorname {\mathrm {End}}(\mathbb {A})$
such that
$s_{0}\in \operatorname {\mathrm {End}}(\mathbb {A})$
such that
![]() $s_{0}(a)=b$
. Since
$s_{0}(a)=b$
. Since
![]() $\mathbb {A}$
has a mobile core, there exist a copy
$\mathbb {A}$
has a mobile core, there exist a copy
![]() $\mathbb {C}$
of the model-complete core of
$\mathbb {C}$
of the model-complete core of
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $g\in \operatorname {\mathrm {End}}(\mathbb {A})$
such that
$g\in \operatorname {\mathrm {End}}(\mathbb {A})$
such that
![]() $a\in g(A)\subseteq C$
. By Lemma 2.6, we know that
$a\in g(A)\subseteq C$
. By Lemma 2.6, we know that
![]() $g(A)=C$
. We set
$g(A)=C$
. We set
![]() $n=\left |{C}\right |$
and write
$n=\left |{C}\right |$
and write
![]() $g(\mathbb {A})=\{a_{1},\dots ,a_{n}\}$
where
$g(\mathbb {A})=\{a_{1},\dots ,a_{n}\}$
where
![]() $a_{1}=a$
. Applying Lemma 2.3, we obtain that the set
$a_{1}=a$
. Applying Lemma 2.3, we obtain that the set
 $$ \begin{align*} V\kern1.4pt{:=}\kern1.4pt\left\{s\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{End}}(\mathbb{A}):s_{0}(a_{1}),\dots,s_{0}(a_{n})\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{Im}}(s)\right\}{=}\kern1.3pt\bigcap_{j=1}^{n}\kern-1pt\left\{s\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{End}}(\mathbb{A}):s_{0}(a_{j})\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{Im}}(s)\kern-1pt\right\} \end{align*} $$
$$ \begin{align*} V\kern1.4pt{:=}\kern1.4pt\left\{s\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{End}}(\mathbb{A}):s_{0}(a_{1}),\dots,s_{0}(a_{n})\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{Im}}(s)\right\}{=}\kern1.3pt\bigcap_{j=1}^{n}\kern-1pt\left\{s\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{End}}(\mathbb{A}):s_{0}(a_{j})\kern1.4pt{\in}\kern1.4pt\operatorname{\mathrm{Im}}(s)\kern-1pt\right\} \end{align*} $$
is open in the Zariski topology. Since the translation
![]() $\rho _{g}\colon s\mapsto sg$
on
$\rho _{g}\colon s\mapsto sg$
on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
is continuous with respect to the Zariski topology, the preimage
$\operatorname {\mathrm {End}}(\mathbb {A})$
is continuous with respect to the Zariski topology, the preimage
is
![]() $\mathcal {T}_{\text {Zariski}}$
-open as well. Again by Lemma 2.6, the images of the endomorphisms
$\mathcal {T}_{\text {Zariski}}$
-open as well. Again by Lemma 2.6, the images of the endomorphisms
![]() $s_{0}g$
and
$s_{0}g$
and
![]() $sg$
(for arbitrary
$sg$
(for arbitrary
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {A})$
) must both have n elements. Hence, the images
$s\in \operatorname {\mathrm {End}}(\mathbb {A})$
) must both have n elements. Hence, the images
![]() $s_{0}(a_{i})$
are pairwise different and, further,
$s_{0}(a_{i})$
are pairwise different and, further,
The crucial observation is that
![]() $Ug=\left \{sg:s\in U\right \}$
is a finite set: Any element
$Ug=\left \{sg:s\in U\right \}$
is a finite set: Any element
![]() $sg$
is determined by the ordered tuple
$sg$
is determined by the ordered tuple
![]() $(s(a_{1}),\dots ,s(a_{n}))$
. Since the unordered set
$(s(a_{1}),\dots ,s(a_{n}))$
. Since the unordered set
![]() $\{s(a_{1}),\dots ,s(a_{n})\}$
is fixed for
$\{s(a_{1}),\dots ,s(a_{n})\}$
is fixed for
![]() $s\in U$
, there are only finitely many (at most
$s\in U$
, there are only finitely many (at most
![]() $n!$
, to be precise) possibilities for the ordered tuple.
$n!$
, to be precise) possibilities for the ordered tuple.
Consequently, the set
![]() $M:=\left \{sg:s\in U, s(a)\neq b\right \}$
is finite as well. We define
$M:=\left \{sg:s\in U, s(a)\neq b\right \}$
is finite as well. We define
and claim that
![]() $O=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):s\in U, s(a)=b\right \}$
, subsequently giving
$O=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):s\in U, s(a)=b\right \}$
, subsequently giving
![]() $s_{0}\in O\subseteq \left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):s(a)=b\right \}$
as desired. If
$s_{0}\in O\subseteq \left \{s\in \operatorname {\mathrm {End}}(\mathbb {A}):s(a)=b\right \}$
as desired. If
![]() $s\in U$
with
$s\in U$
with
![]() $s(a)=b$
, then we take
$s(a)=b$
, then we take
![]() $z\in A$
with
$z\in A$
with
![]() $g(z)=a$
and note
$g(z)=a$
and note
![]() $sg(z)=s(a)=b\neq t(z)$
for all
$sg(z)=s(a)=b\neq t(z)$
for all
![]() $t\in M$
. Conversely, if
$t\in M$
. Conversely, if
![]() $s\in U$
but
$s\in U$
but
![]() $s(a)\neq b$
, then
$s(a)\neq b$
, then
![]() $t:=sg\in M$
, so
$t:=sg\in M$
, so
![]() $s\notin O$
—completing the proof.
$s\notin O$
—completing the proof.
3.3 Cores without algebraicity
Now we consider structures
![]() $\mathbb {A}$
whose model-complete cores do not have algebraicity. In our proof, we will use the following technical condition from [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9]:
$\mathbb {A}$
whose model-complete cores do not have algebraicity. In our proof, we will use the following technical condition from [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9]:
Lemma 3.5 [Reference Elliott, Jonušas, Mesyan, Mitchell, Morayne and Péresse9, Lemma 5.3].
Let X be an infinite set and let S be a subsemigroup of
![]() $X^{X}$
such that for every
$X^{X}$
such that for every
![]() $a\in X$
there exist
$a\in X$
there exist
![]() $\alpha ,\beta ,\gamma _{1},\dots ,\gamma _{n}\in S$
for some
$\alpha ,\beta ,\gamma _{1},\dots ,\gamma _{n}\in S$
for some
![]() $n\in \mathbb {N}$
such that the following hold:
$n\in \mathbb {N}$
such that the following hold:
-
(i)
 $\alpha \vert _{X\setminus \{a\}}=\beta \vert _{X\setminus \{a\}}$
and
$\alpha \vert _{X\setminus \{a\}}=\beta \vert _{X\setminus \{a\}}$
and
 $\alpha (a)\neq \beta (a)$
;
$\alpha (a)\neq \beta (a)$
; -
(ii)
 $a\in \operatorname {\mathrm {Im}}(\gamma _{i})$
for all
$a\in \operatorname {\mathrm {Im}}(\gamma _{i})$
for all
 $i\in \{1,\dots ,n\}$
;
$i\in \{1,\dots ,n\}$
; -
(iii) For every
 $s\in S$
and every
$s\in S$
and every
 $x\in X\setminus \{s(a)\}$
, there is
$x\in X\setminus \{s(a)\}$
, there is
 $i\in \{1,\dots ,n\}$
so that
$i\in \{1,\dots ,n\}$
so that
 $\operatorname {\mathrm {Im}}(\gamma _{i})\cap s^{-1}(x)=\emptyset $
.
$\operatorname {\mathrm {Im}}(\gamma _{i})\cap s^{-1}(x)=\emptyset $
.
Then the Zariski topology of S is the pointwise topology.
We remark that (i) corresponds to Lemma 2.2 and that the proof proceeds by constructing the generating sets of the pointwise topology from the sets
![]() $\left \{s\in S:a\in \operatorname {\mathrm {Im}}(s)\right \}$
exhibited in Lemma 2.3.
$\left \{s\in S:a\in \operatorname {\mathrm {Im}}(s)\right \}$
exhibited in Lemma 2.3.
The fact that the model-complete core does not have algebraicity will come into play via the following observation:
Lemma 3.6. Let
![]() $\mathbb {B}$
be a countably infinite structure without algebraicity and let
$\mathbb {B}$
be a countably infinite structure without algebraicity and let
![]() $b\in \mathbb {B}$
. Then there exist
$b\in \mathbb {B}$
. Then there exist
![]() $f,h$
in the
$f,h$
in the
![]() $\mathcal {T}_{pw}$
-closure of
$\mathcal {T}_{pw}$
-closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {B})$
such that
$\operatorname {\mathrm {Aut}}(\mathbb {B})$
such that
![]() $f(b)=b=h(b)$
and
$f(b)=b=h(b)$
and
![]() $f(B)\cap h(B)=\{b\}$
(so there exist two copies of
$f(B)\cap h(B)=\{b\}$
(so there exist two copies of
![]() $\mathbb {B}$
within
$\mathbb {B}$
within
![]() $\mathbb {B}$
which only have b in common).
$\mathbb {B}$
which only have b in common).
Proof We enumerate
![]() $B=\left \{b_{n}:n\in \mathbb {N}\right \}$
where
$B=\left \{b_{n}:n\in \mathbb {N}\right \}$
where
![]() $b_{0}=b$
. First, we recursively construct automorphisms
$b_{0}=b$
. First, we recursively construct automorphisms
![]() $\alpha _{n},\beta _{n}\in \operatorname {\mathrm {Aut}}(\mathbb {B})$
,
$\alpha _{n},\beta _{n}\in \operatorname {\mathrm {Aut}}(\mathbb {B})$
,
![]() $n\in \mathbb {N}$
, such that
$n\in \mathbb {N}$
, such that
![]() $\alpha _{n+1}\vert _{\{b_{0},\dots ,b_{n}\}}=\alpha _{n}\vert _{\{b_{0},\dots ,b_{n}\}}$
,
$\alpha _{n+1}\vert _{\{b_{0},\dots ,b_{n}\}}=\alpha _{n}\vert _{\{b_{0},\dots ,b_{n}\}}$
,
![]() $\beta _{n+1}\vert _{\{b_{0},\dots ,b_{n}\}}=\beta _{n}\vert _{\{b_{0},\dots ,b_{n}\}}$
, and
$\beta _{n+1}\vert _{\{b_{0},\dots ,b_{n}\}}=\beta _{n}\vert _{\{b_{0},\dots ,b_{n}\}}$
, and
![]() $\alpha _{n}(\{b_{0},\dots ,b_{n}\})\cap \beta _{n}(\{b_{0},\dots ,b_{n}\})=\{b\}$
for all
$\alpha _{n}(\{b_{0},\dots ,b_{n}\})\cap \beta _{n}(\{b_{0},\dots ,b_{n}\})=\{b\}$
for all
![]() $n\in \mathbb {N}$
. We start by setting
$n\in \mathbb {N}$
. We start by setting
![]() $\alpha _{0}=\beta _{0}:=\operatorname {\mathrm {id}}_{B}$
. If
$\alpha _{0}=\beta _{0}:=\operatorname {\mathrm {id}}_{B}$
. If
![]() $\alpha _{n}$
and
$\alpha _{n}$
and
![]() $\beta _{n}$
are already defined, we put
$\beta _{n}$
are already defined, we put
![]() $Y:=\alpha _{n}(\{b_{0},\dots ,b_{n}\})$
as well as
$Y:=\alpha _{n}(\{b_{0},\dots ,b_{n}\})$
as well as
![]() $Z:=\beta _{n}(\{b_{0},\dots ,b_{n}\})$
. Since
$Z:=\beta _{n}(\{b_{0},\dots ,b_{n}\})$
. Since
![]() $\mathbb {B}$
has no algebraicity, the relative orbits
$\mathbb {B}$
has no algebraicity, the relative orbits
![]() $\operatorname {\mathrm {Orb}}(\alpha _{n}(b_{n+1});Y)$
and
$\operatorname {\mathrm {Orb}}(\alpha _{n}(b_{n+1});Y)$
and
![]() $\operatorname {\mathrm {Orb}}(\beta _{n}(b_{n+1});Z)$
are infinite, so we can find
$\operatorname {\mathrm {Orb}}(\beta _{n}(b_{n+1});Z)$
are infinite, so we can find
![]() $c_{n+1}\in \operatorname {\mathrm {Orb}}(\alpha _{n}(b_{n+1});Y)$
which is not contained in Z and then find
$c_{n+1}\in \operatorname {\mathrm {Orb}}(\alpha _{n}(b_{n+1});Y)$
which is not contained in Z and then find
![]() $d_{n+1}\in \operatorname {\mathrm {Orb}}(\beta _{n}(b_{n+1});Z)$
which is not contained in
$d_{n+1}\in \operatorname {\mathrm {Orb}}(\beta _{n}(b_{n+1});Z)$
which is not contained in
![]() $Y\cup \{c_{n+1}\}$
. Taking
$Y\cup \{c_{n+1}\}$
. Taking
![]() $\gamma \in \operatorname {\mathrm {Stab}}(Y)$
with
$\gamma \in \operatorname {\mathrm {Stab}}(Y)$
with
![]() $\gamma (\alpha _{n}(b_{n+1}))=c_{n+1}$
as well as
$\gamma (\alpha _{n}(b_{n+1}))=c_{n+1}$
as well as
![]() $\delta \in \operatorname {\mathrm {Stab}}(Z)$
with
$\delta \in \operatorname {\mathrm {Stab}}(Z)$
with
![]() $\delta (\beta _{n}(b_{n+1}))=d_{n+1}$
, and setting
$\delta (\beta _{n}(b_{n+1}))=d_{n+1}$
, and setting
![]() $\alpha _{n+1}:=\gamma \alpha _{n}$
as well as
$\alpha _{n+1}:=\gamma \alpha _{n}$
as well as
![]() $\beta _{n+1}:=\delta \beta _{n}$
completes the construction. Finally, we set
$\beta _{n+1}:=\delta \beta _{n}$
completes the construction. Finally, we set
![]() $f:=\lim _{n\in \mathbb {N}}\alpha _{n}$
and
$f:=\lim _{n\in \mathbb {N}}\alpha _{n}$
and
![]() $h:=\lim _{n\in \mathbb {N}}\beta _{n}$
; these maps are contained in the
$h:=\lim _{n\in \mathbb {N}}\beta _{n}$
; these maps are contained in the
![]() $\mathcal {T}_{pw}$
-closure of
$\mathcal {T}_{pw}$
-closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {B})$
and have the desired properties.
$\operatorname {\mathrm {Aut}}(\mathbb {B})$
and have the desired properties.
Proposition 3.7. Let
![]() $\mathbb {A}$
be an
$\mathbb {A}$
be an
![]() $\omega $
-categorical structure without algebraicity which has a mobile core. If the model-complete core of
$\omega $
-categorical structure without algebraicity which has a mobile core. If the model-complete core of
![]() $\mathbb {A}$
is infinite and does not have algebraicity, then the Zariski topology on
$\mathbb {A}$
is infinite and does not have algebraicity, then the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
coincides with the pointwise topology.
$\operatorname {\mathrm {End}}(\mathbb {A})$
coincides with the pointwise topology.
Proof We check the assumptions of Lemma 3.5.
Since
![]() $\mathbb {A}$
is
$\mathbb {A}$
is
![]() $\omega $
-categorical without algebraicity, property (i) follows from Lemma 2.2.
$\omega $
-categorical without algebraicity, property (i) follows from Lemma 2.2.
For properties (ii) and (iii), we fix
![]() $a\in A$
, set
$a\in A$
, set
![]() $n=2$
, and construct
$n=2$
, and construct
![]() $\gamma _{1},\gamma _{2}$
. Since
$\gamma _{1},\gamma _{2}$
. Since
![]() $\mathbb {A}$
has a mobile core, there exist a copy
$\mathbb {A}$
has a mobile core, there exist a copy
![]() $\mathbb {C}$
of the model-complete core of
$\mathbb {C}$
of the model-complete core of
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $g\in \operatorname {\mathrm {End}}(\mathbb {A})$
such that
$g\in \operatorname {\mathrm {End}}(\mathbb {A})$
such that
![]() $a\in g(A)\subseteq C$
. Since
$a\in g(A)\subseteq C$
. Since
![]() $\mathbb {C}$
has no algebraicity, there exist
$\mathbb {C}$
has no algebraicity, there exist
![]() $f,h$
in the
$f,h$
in the
![]() $\mathcal {T}_{pw}$
-closure of
$\mathcal {T}_{pw}$
-closure of
![]() $\operatorname {\mathrm {Aut}}(\mathbb {C})$
such that
$\operatorname {\mathrm {Aut}}(\mathbb {C})$
such that
![]() $f(a)=a=h(a)$
and
$f(a)=a=h(a)$
and
![]() $f(C)\cap h(C)=\{a\}$
by Lemma 3.6. Using the homomorphism
$f(C)\cap h(C)=\{a\}$
by Lemma 3.6. Using the homomorphism
![]() $g\colon \mathbb {A}\to \mathbb {C}$
, we set
$g\colon \mathbb {A}\to \mathbb {C}$
, we set
![]() $\gamma _{1}:=fg$
and
$\gamma _{1}:=fg$
and
![]() $\gamma _{2}:=hg$
, considered as endomorphisms of
$\gamma _{2}:=hg$
, considered as endomorphisms of
![]() $\mathbb {A}$
. Then
$\mathbb {A}$
. Then
![]() $a\in \operatorname {\mathrm {Im}}(\gamma _{i})$
, i.e., (ii) holds. Suppose now that for some
$a\in \operatorname {\mathrm {Im}}(\gamma _{i})$
, i.e., (ii) holds. Suppose now that for some
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {A})$
and
$s\in \operatorname {\mathrm {End}}(\mathbb {A})$
and
![]() $x\in A$
, we have
$x\in A$
, we have
![]() $\operatorname {\mathrm {Im}}(\gamma _{i})\cap s^{-1}\{x\}\neq \emptyset $
for
$\operatorname {\mathrm {Im}}(\gamma _{i})\cap s^{-1}\{x\}\neq \emptyset $
for
![]() $i=1,2$
. In order to prove (iii), the goal is to show
$i=1,2$
. In order to prove (iii), the goal is to show
![]() $x=s(a)$
. We rewrite to obtain the existence of
$x=s(a)$
. We rewrite to obtain the existence of
![]() $x_{i}\in A$
with
$x_{i}\in A$
with
![]() $sfg(x_{1})=s\gamma _{1}(x_{1})=x=s\gamma _{2}(x_{2})=shg(x_{2})$
. As a homomorphism from
$sfg(x_{1})=s\gamma _{1}(x_{1})=x=s\gamma _{2}(x_{2})=shg(x_{2})$
. As a homomorphism from
![]() $\mathbb {C}$
to
$\mathbb {C}$
to
![]() $\mathbb {A}$
, the restriction
$\mathbb {A}$
, the restriction
![]() $s\vert _{C}:\mathbb {C}\to \mathbb {A}$
is an embedding by Lemma 2.5, in particular injective. Hence,
$s\vert _{C}:\mathbb {C}\to \mathbb {A}$
is an embedding by Lemma 2.5, in particular injective. Hence,
yielding
![]() $x=sfg(x_{1})=s(a)$
as desired.
$x=sfg(x_{1})=s(a)$
as desired.
4 Counterexample
In this section, we give an example of an
![]() $\omega $
-categorical (even homogeneous in a finite language) and transitive structure without algebraicity such that the Zariski topology on its endomorphism monoid does not coincide with the pointwise topology, thus answering Question 1.1. By our results in Section 3, the model-complete core of this structure must be infinite and have algebraicity. Informally speaking, we take a complete graph on countably many vertices where each point has as fine structure a complete bipartite graph on countably many vertices (see Figure 1).
$\omega $
-categorical (even homogeneous in a finite language) and transitive structure without algebraicity such that the Zariski topology on its endomorphism monoid does not coincide with the pointwise topology, thus answering Question 1.1. By our results in Section 3, the model-complete core of this structure must be infinite and have algebraicity. Informally speaking, we take a complete graph on countably many vertices where each point has as fine structure a complete bipartite graph on countably many vertices (see Figure 1).

Figure 1 The structure
![]() $\mathbb {G}$
: complete graph on countably many vertices (dashed) where each point has a complete bipartite graph on countably many vertices as fine structure (solid).
$\mathbb {G}$
: complete graph on countably many vertices (dashed) where each point has a complete bipartite graph on countably many vertices as fine structure (solid).
4.1 Definitions, notation, and preliminary properties
We start by formally introducing our structure and giving some notation.
Definition 4.1.
-
(i) Let
 $\mathbb {K}_{2,\omega }$
denote the complete irreflexive bipartite graph on countably many vertices: We write the domain as
$\mathbb {K}_{2,\omega }$
denote the complete irreflexive bipartite graph on countably many vertices: We write the domain as
 $K_{2,\omega }:=A_{+1}\mathbin {\dot {\cup }} A_{-1}$
where
$K_{2,\omega }:=A_{+1}\mathbin {\dot {\cup }} A_{-1}$
where
 $A_{+1}$
and
$A_{+1}$
and
 $A_{-1}$
are countably infinite sets referred to as the parts of
$A_{-1}$
are countably infinite sets referred to as the parts of
 $\mathbb {K}_{2,\omega }$
, and define the edge relation as
$\mathbb {K}_{2,\omega }$
, and define the edge relation as
 $E^{\mathbb {K}_{2,\omega }}:=A_{-1}\times A_{+1}\cup A_{+1}\times A_{-1}$
, i.e., two points are connected if and only if they are contained in different parts of
$E^{\mathbb {K}_{2,\omega }}:=A_{-1}\times A_{+1}\cup A_{+1}\times A_{-1}$
, i.e., two points are connected if and only if they are contained in different parts of
 $\mathbb {K}_{2,\omega }$
.
$\mathbb {K}_{2,\omega }$
. -
(ii) Let
 $\mathbb {G}$
denote the following structure over the language of two binary relations: We set
$\mathbb {G}$
denote the following structure over the language of two binary relations: We set
 $G:=\mathbb {N}\times K_{2,\omega }$
(countably many copies of
$G:=\mathbb {N}\times K_{2,\omega }$
(countably many copies of
 $K_{2,\omega }$
) and define the relations as follows: This means that the set of copies of
$K_{2,\omega }$
) and define the relations as follows: This means that the set of copies of $$ \begin{align*} E_{1}^{\mathbb{G}}&:=\left\{((i,x),(j,y))\in G^{2}:i\neq j\right\},\\ E_{2}^{\mathbb{G}}&:=\left\{((i,x),(j,y))\in G^{2}:i=j\text{ and }(x,y)\in E^{\mathbb{K}_{2,\omega}}\right\}. \end{align*} $$
$$ \begin{align*} E_{1}^{\mathbb{G}}&:=\left\{((i,x),(j,y))\in G^{2}:i\neq j\right\},\\ E_{2}^{\mathbb{G}}&:=\left\{((i,x),(j,y))\in G^{2}:i=j\text{ and }(x,y)\in E^{\mathbb{K}_{2,\omega}}\right\}. \end{align*} $$
 $K_{2,\omega }$
forms a complete graph with respect to
$K_{2,\omega }$
forms a complete graph with respect to
 $E_{1}$
and that each copy
$E_{1}$
and that each copy
 $\{i\}\times K_{2,\omega }$
of
$\{i\}\times K_{2,\omega }$
of
 $K_{2,\omega }$
is indeed a copy of the graph
$K_{2,\omega }$
is indeed a copy of the graph
 $\mathbb {K}_{2,\omega }$
(with respect to
$\mathbb {K}_{2,\omega }$
(with respect to
 $E_{2}$
) (see Figure 1).
$E_{2}$
) (see Figure 1).
Note that an endomorphism s of
![]() $\mathbb {K}_{2,\omega }$
acts as a permutation on the set
$\mathbb {K}_{2,\omega }$
acts as a permutation on the set
![]() $\{A_{+1},A_{-1}\}$
of parts since two (
$\{A_{+1},A_{-1}\}$
of parts since two (
![]() $E_{2}^{\mathbb {K}_{2,\omega }}$
-connected) elements from different parts of
$E_{2}^{\mathbb {K}_{2,\omega }}$
-connected) elements from different parts of
![]() $\mathbb {K}_{2,\omega }$
cannot be mapped to the same part of
$\mathbb {K}_{2,\omega }$
cannot be mapped to the same part of
![]() $\mathbb {K}_{2,\omega }$
– we either have
$\mathbb {K}_{2,\omega }$
– we either have
![]() $s(A_{+1})\subseteq A_{+1}$
and
$s(A_{+1})\subseteq A_{+1}$
and
![]() $s(A_{-1})\subseteq A_{-1}$
or
$s(A_{-1})\subseteq A_{-1}$
or
![]() $s(A_{+1})\subseteq A_{-1}$
and
$s(A_{+1})\subseteq A_{-1}$
and
![]() $s(A_{-1})\subseteq A_{+1}$
.
$s(A_{-1})\subseteq A_{+1}$
.
Definition 4.2. For
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
, we put
$s\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
, we put
![]() $\operatorname {\mathrm {sgn}}(s)\in \{+1,-1\}$
to be the sign of the permutation induced by s on
$\operatorname {\mathrm {sgn}}(s)\in \{+1,-1\}$
to be the sign of the permutation induced by s on
![]() $\{A_{+1},A_{-1}\}$
. Explicitly, this means that
$\{A_{+1},A_{-1}\}$
. Explicitly, this means that
![]() $s(A_{e})\subseteq A_{e\cdot \operatorname {\mathrm {sgn}}(s)}$
for
$s(A_{e})\subseteq A_{e\cdot \operatorname {\mathrm {sgn}}(s)}$
for
![]() $e=\pm 1$
. As a slight abuse of notation, we will refer to
$e=\pm 1$
. As a slight abuse of notation, we will refer to
![]() $\operatorname {\mathrm {sgn}}(s)$
as the sign of s.
$\operatorname {\mathrm {sgn}}(s)$
as the sign of s.
Clearly, we have
![]() $\operatorname {\mathrm {sgn}}(st)=\operatorname {\mathrm {sgn}}(s)\operatorname {\mathrm {sgn}}(t)$
for
$\operatorname {\mathrm {sgn}}(st)=\operatorname {\mathrm {sgn}}(s)\operatorname {\mathrm {sgn}}(t)$
for
![]() $s,t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
. As a tool, we define two very simple endomorphisms of
$s,t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
. As a tool, we define two very simple endomorphisms of
![]() $\mathbb {K}_{2,\omega }$
.
$\mathbb {K}_{2,\omega }$
.
Notation 4.3.
-
(i) In the sequel,
 $a_{+1}\in A_{+1}$
and
$a_{+1}\in A_{+1}$
and
 $a_{-1}\in A_{-1}$
shall denote fixed elements.
$a_{-1}\in A_{-1}$
shall denote fixed elements. -
(ii) We define
 $c_{+1}\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
and
$c_{+1}\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
and
 $c_{-1}\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
to be the unique endomorphisms of
$c_{-1}\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
to be the unique endomorphisms of
 $\mathbb {K}_{2,\omega }$
with image
$\mathbb {K}_{2,\omega }$
with image
 $\{a_{+1},a_{-1}\}$
and sign
$\{a_{+1},a_{-1}\}$
and sign
 $+1$
and
$+1$
and
 $-1$
, respectively. So
$-1$
, respectively. So
 $c_{+1}$
is constant on
$c_{+1}$
is constant on
 $A_{e}$
with value
$A_{e}$
with value
 $a_{e}$
and
$a_{e}$
and
 $c_{-1}$
is constant on
$c_{-1}$
is constant on
 $A_{e}$
with value
$A_{e}$
with value
 $a_{-e}$
for
$a_{-e}$
for
 $e=\pm 1$
.
$e=\pm 1$
.
In order to describe the automorphism group and endomorphism monoid of
![]() $\mathbb {G}$
, the following notation will be useful.
$\mathbb {G}$
, the following notation will be useful.
Notation 4.4. Let X be a set, let
![]() $\tau \colon \mathbb {N}\to \mathbb {N}$
, and let
$\tau \colon \mathbb {N}\to \mathbb {N}$
, and let
![]() $s_{i}\colon X\to X$
for each
$s_{i}\colon X\to X$
for each
![]() $i\in \mathbb {N}$
. Then
$i\in \mathbb {N}$
. Then
![]() $\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
shall denote the self-map of
$\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
shall denote the self-map of
![]() $\mathbb {N}\times X$
defined by
$\mathbb {N}\times X$
defined by
 $$ \begin{align*} \bigsqcup_{i\in\mathbb{N}}\! ^{\tau} s_{i}: \begin{cases} \mathbb{N}\times X,&\to\mathbb{N}\times X,\\ \hfill (i,x),&\mapsto (\tau(i),s_{i}(x)). \end{cases} \end{align*} $$
$$ \begin{align*} \bigsqcup_{i\in\mathbb{N}}\! ^{\tau} s_{i}: \begin{cases} \mathbb{N}\times X,&\to\mathbb{N}\times X,\\ \hfill (i,x),&\mapsto (\tau(i),s_{i}(x)). \end{cases} \end{align*} $$
For
![]() $\tau \colon \mathbb {N}\to \mathbb {N}$
and
$\tau \colon \mathbb {N}\to \mathbb {N}$
and
![]() $s\colon X\to X$
, we further set
$s\colon X\to X$
, we further set
![]() $\tau \ltimes s:=\bigsqcup _{i\in \mathbb {N}}^{\tau }s$
.
$\tau \ltimes s:=\bigsqcup _{i\in \mathbb {N}}^{\tau }s$
.
Lemma 4.5.
-
(i)
 $\operatorname {\mathrm {End}}(\mathbb {G})=\left \{\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}:\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}),s_{i}\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })\right \}$
.
$\operatorname {\mathrm {End}}(\mathbb {G})=\left \{\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}:\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}),s_{i}\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })\right \}$
. -
(ii)
 $\operatorname {\mathrm {Aut}}(\mathbb {G})=\left \{\bigsqcup _{i\in \mathbb {N}}^{\sigma } \alpha _{i}:\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {N}),\alpha _{i}\in \operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })\right \}$
.
$\operatorname {\mathrm {Aut}}(\mathbb {G})=\left \{\bigsqcup _{i\in \mathbb {N}}^{\sigma } \alpha _{i}:\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {N}),\alpha _{i}\in \operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })\right \}$
.
Remark 4.6. Lemma 4.5 exactly expresses that
![]() $\operatorname {\mathrm {End}}(\mathbb {G})$
and
$\operatorname {\mathrm {End}}(\mathbb {G})$
and
![]() $\operatorname {\mathrm {Aut}}(\mathbb {G})$
are the (unrestricted) wreath products of
$\operatorname {\mathrm {Aut}}(\mathbb {G})$
are the (unrestricted) wreath products of
![]() $\operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
with
$\operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
with
![]() $\operatorname {\mathrm {Inj}}(\mathbb {N})$
and
$\operatorname {\mathrm {Inj}}(\mathbb {N})$
and
![]() $\operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
with
$\operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
with
![]() $\operatorname {\mathrm {Sym}}(\mathbb {N})$
, respectively, by the canonical actions of
$\operatorname {\mathrm {Sym}}(\mathbb {N})$
, respectively, by the canonical actions of
![]() $\operatorname {\mathrm {Inj}}(\mathbb {N})$
and
$\operatorname {\mathrm {Inj}}(\mathbb {N})$
and
![]() $\operatorname {\mathrm {Sym}}(\mathbb {N})$
on
$\operatorname {\mathrm {Sym}}(\mathbb {N})$
on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Proof (of Lemma 4.5)
It is straightforward to see that the maps
![]() $\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
in (i) and
$\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
in (i) and
![]() $\bigsqcup _{i\in \mathbb {N}}^{\sigma }\alpha _{i}$
in (ii) form endomorphisms and automorphisms, respectively. Thus, (ii) follows immediately from (i) since
$\bigsqcup _{i\in \mathbb {N}}^{\sigma }\alpha _{i}$
in (ii) form endomorphisms and automorphisms, respectively. Thus, (ii) follows immediately from (i) since
![]() $\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
can only be bijective if
$\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
can only be bijective if
![]() $\tau \in \operatorname {\mathrm {Sym}}(\mathbb {N})$
and
$\tau \in \operatorname {\mathrm {Sym}}(\mathbb {N})$
and
![]() $s_{i}\in \operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
.
$s_{i}\in \operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
.
To show (i), we first note that for any
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
and any two elements
$s\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
and any two elements
![]() $(i,x),(i,y)\in G$
in the same copy of
$(i,x),(i,y)\in G$
in the same copy of
![]() $K_{2,\omega }$
, the images
$K_{2,\omega }$
, the images
![]() $s(i,x)$
and
$s(i,x)$
and
![]() $s(i,y)$
are also contained in the same copy of
$s(i,y)$
are also contained in the same copy of
![]() $K_{2,\omega }$
: Either
$K_{2,\omega }$
: Either
![]() $x,y$
are connected in
$x,y$
are connected in
![]() $\mathbb {K}_{2,\omega }$
in which case
$\mathbb {K}_{2,\omega }$
in which case
![]() $s(i,x)$
and
$s(i,x)$
and
![]() $s(i,y)$
are
$s(i,y)$
are
![]() $E_{2}^{\mathbb {G}}$
-connected and therefore contained in the same copy, or
$E_{2}^{\mathbb {G}}$
-connected and therefore contained in the same copy, or
![]() $x,y$
are both connected in
$x,y$
are both connected in
![]() $\mathbb {K}_{2,\omega }$
to a common element z in which case
$\mathbb {K}_{2,\omega }$
to a common element z in which case
![]() $s(i,x)$
and
$s(i,x)$
and
![]() $s(i,y)$
are both
$s(i,y)$
are both
![]() $E_{2}^{\mathbb {G}}$
-connected to
$E_{2}^{\mathbb {G}}$
-connected to
![]() $s(i,z)$
and therefore contained in the same copy. Setting
$s(i,z)$
and therefore contained in the same copy. Setting
![]() $\tau (i)$
to be the index of this copy, i.e.,
$\tau (i)$
to be the index of this copy, i.e.,
![]() $s(i,x),s(i,y)\in \{\tau (i)\}\times K_{2,\omega }$
, we obtain that s can be written as
$s(i,x),s(i,y)\in \{\tau (i)\}\times K_{2,\omega }$
, we obtain that s can be written as
![]() $\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
for some functions
$\bigsqcup _{i\in \mathbb {N}}^{\tau } s_{i}$
for some functions
![]() $s_{i}\colon K_{2,\omega }\to K_{2,\omega }$
. By compatibility of s with
$s_{i}\colon K_{2,\omega }\to K_{2,\omega }$
. By compatibility of s with
![]() $E_{1}^{\mathbb {G}}$
, the map
$E_{1}^{\mathbb {G}}$
, the map
![]() $\tau $
needs to be injective. Further, the maps
$\tau $
needs to be injective. Further, the maps
![]() $s_{i}$
are endomorphisms of
$s_{i}$
are endomorphisms of
![]() $\mathbb {K}_{2,\omega }$
since s is compatible with
$\mathbb {K}_{2,\omega }$
since s is compatible with
![]() $E_{2}^{\mathbb {G}}$
.
$E_{2}^{\mathbb {G}}$
.
The representation in (ii) readily yields the following properties of
![]() $\mathbb {G}$
by means of lifting from
$\mathbb {G}$
by means of lifting from
![]() $\operatorname {\mathrm {Sym}}(\mathbb {N})$
and
$\operatorname {\mathrm {Sym}}(\mathbb {N})$
and
![]() $\operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
:
$\operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
:
Lemma 4.7.
![]() $\mathbb {G}$
is
$\mathbb {G}$
is
![]() $\omega $
-categorical, homogeneous, transitive, and has no algebraicity.
$\omega $
-categorical, homogeneous, transitive, and has no algebraicity.
Proof We start by showing that
![]() $\mathbb {G}$
is homogeneous which will also yield the
$\mathbb {G}$
is homogeneous which will also yield the
![]() $\omega $
-categoricity since
$\omega $
-categoricity since
![]() $\mathbb {G}$
has a finite language. Let
$\mathbb {G}$
has a finite language. Let
![]() $\bar {a}=(a_{1},\dots ,a_{n})$
and
$\bar {a}=(a_{1},\dots ,a_{n})$
and
![]() $\bar {b}=(b_{1},\dots ,b_{n})$
be tuples in G and let
$\bar {b}=(b_{1},\dots ,b_{n})$
be tuples in G and let
![]() $m\colon \bar {a}\mapsto \bar {b}$
be a finite partial isomorphism. Writing
$m\colon \bar {a}\mapsto \bar {b}$
be a finite partial isomorphism. Writing
![]() ${a_{k}=(i_{k},x_{k})}$
and
${a_{k}=(i_{k},x_{k})}$
and
![]() $b_{k}=(j_{k},y_{k})$
, we note that
$b_{k}=(j_{k},y_{k})$
, we note that
![]() $i_{k}$
and
$i_{k}$
and
![]() $i_{\ell }$
coincide if and only if
$i_{\ell }$
coincide if and only if
![]() $j_{k}$
and
$j_{k}$
and
![]() $j_{\ell }$
coincide (for otherwise, either m or
$j_{\ell }$
coincide (for otherwise, either m or
![]() $m^{-1}$
would not be compatible with
$m^{-1}$
would not be compatible with
![]() $E_{1}^{\mathbb {G}}$
). Hence, the map
$E_{1}^{\mathbb {G}}$
). Hence, the map
![]() $i_{k}\mapsto j_{k}$
is a well-defined finite partial bijection and can thus easily be extended to some
$i_{k}\mapsto j_{k}$
is a well-defined finite partial bijection and can thus easily be extended to some
![]() $\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {N})$
(in other words, the structure with domain
$\sigma \in \operatorname {\mathrm {Sym}}(\mathbb {N})$
(in other words, the structure with domain
![]() $\mathbb {N}$
and without any relations is homogeneous). Further, if
$\mathbb {N}$
and without any relations is homogeneous). Further, if
![]() $i_{k_{1}}=\cdots =i_{k_{N}}=:i$
, then
$i_{k_{1}}=\cdots =i_{k_{N}}=:i$
, then
![]() $m_{i}\colon x_{k_{1}}\mapsto y_{k_{1}},\dots ,x_{k_{N}}\mapsto y_{k_{N}}$
is a finite partial isomorphism of
$m_{i}\colon x_{k_{1}}\mapsto y_{k_{1}},\dots ,x_{k_{N}}\mapsto y_{k_{N}}$
is a finite partial isomorphism of
![]() $\mathbb {K}_{2,\omega }$
since m is a finite partial isomorphism with respect to
$\mathbb {K}_{2,\omega }$
since m is a finite partial isomorphism with respect to
![]() $E_{2}^{\mathbb {G}}$
. The graph
$E_{2}^{\mathbb {G}}$
. The graph
![]() $\mathbb {K}_{2,\omega }$
is homogeneous, so
$\mathbb {K}_{2,\omega }$
is homogeneous, so
![]() $m_{i}$
extends to
$m_{i}$
extends to
![]() $\alpha _{i}\in \operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
. Setting
$\alpha _{i}\in \operatorname {\mathrm {Aut}}(\mathbb {K}_{2,\omega })$
. Setting
![]() $\alpha _{i}=\operatorname {\mathrm {id}}_{K_{2,\omega }}$
for all i such that no
$\alpha _{i}=\operatorname {\mathrm {id}}_{K_{2,\omega }}$
for all i such that no
![]() $x_{k}$
is contained in the i-th copy of
$x_{k}$
is contained in the i-th copy of
![]() $K_{2,\omega }$
and putting
$K_{2,\omega }$
and putting
![]() $\alpha :=\bigsqcup _{i\in \mathbb {N}}^{\sigma }\alpha _{i}\in \operatorname {\mathrm {Aut}}(\mathbb {G})$
, we obtain an extension of m.
$\alpha :=\bigsqcup _{i\in \mathbb {N}}^{\sigma }\alpha _{i}\in \operatorname {\mathrm {Aut}}(\mathbb {G})$
, we obtain an extension of m.
Next, observe that
![]() $\mathbb {G}$
is transitive: given
$\mathbb {G}$
is transitive: given
![]() $a,b\in G$
, the map
$a,b\in G$
, the map
![]() $a\mapsto b$
is a finite partial isomorphism since neither
$a\mapsto b$
is a finite partial isomorphism since neither
![]() $E_{1}^{\mathbb {G}}$
nor
$E_{1}^{\mathbb {G}}$
nor
![]() $E_{2}^{\mathbb {G}}$
contain any loops. Thus, homogeneity yields
$E_{2}^{\mathbb {G}}$
contain any loops. Thus, homogeneity yields
![]() $\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {G})$
with
$\alpha \in \operatorname {\mathrm {Aut}}(\mathbb {G})$
with
![]() $\alpha (a)=b$
.
$\alpha (a)=b$
.
Finally,
![]() $\mathbb {G}$
does not have algebraicity since
$\mathbb {G}$
does not have algebraicity since
![]() $\mathbb {K}_{2,\omega }$
does not have algebraicity: For a finite set
$\mathbb {K}_{2,\omega }$
does not have algebraicity: For a finite set
![]() $Y\subseteq G$
and
$Y\subseteq G$
and
![]() $a=(i_{0},x_{0})\in G\setminus Y$
, we set
$a=(i_{0},x_{0})\in G\setminus Y$
, we set
![]() $Y_{i_{0}}:=\left \{y\in K_{2,\omega }:(i_{0},y)\in Y\right \}\not \ni x_{0}$
and note that
$Y_{i_{0}}:=\left \{y\in K_{2,\omega }:(i_{0},y)\in Y\right \}\not \ni x_{0}$
and note that
![]() $\operatorname {\mathrm {Orb}}_{\mathbb {G}}(a;Y)$
encompasses the infinite set
$\operatorname {\mathrm {Orb}}_{\mathbb {G}}(a;Y)$
encompasses the infinite set
![]() $\{i_{0}\}\times \operatorname {\mathrm {Orb}}_{\mathbb {K}_{2,\omega }}(x_{0};Y_{i_{0}})$
as witnessed by the automorphisms
$\{i_{0}\}\times \operatorname {\mathrm {Orb}}_{\mathbb {K}_{2,\omega }}(x_{0};Y_{i_{0}})$
as witnessed by the automorphisms
![]() $\bigsqcup _{i\in \mathbb {N}}^{\operatorname {\mathrm {id}}}\alpha _{i}$
where
$\bigsqcup _{i\in \mathbb {N}}^{\operatorname {\mathrm {id}}}\alpha _{i}$
where
![]() $\alpha _{i_{0}}\in \operatorname {\mathrm {Stab}}_{\mathbb {K}_{2,\omega }}(Y_{i_{0}})$
and
$\alpha _{i_{0}}\in \operatorname {\mathrm {Stab}}_{\mathbb {K}_{2,\omega }}(Y_{i_{0}})$
and
![]() $\alpha _{i}=\operatorname {\mathrm {id}}_{K_{2,\omega }}$
for
$\alpha _{i}=\operatorname {\mathrm {id}}_{K_{2,\omega }}$
for
![]() $i\neq i_{0}$
.
$i\neq i_{0}$
.
Remark 4.8. An alternative construction of
![]() $\mathbb {G}$
is as a first-order reduct of the free superposition (see [Reference Bodirsky6]; this is a type of construction to combine two structures with different signatures in a “free” way) of
$\mathbb {G}$
is as a first-order reduct of the free superposition (see [Reference Bodirsky6]; this is a type of construction to combine two structures with different signatures in a “free” way) of
![]() $\mathbb {K}_{2,\omega }$
with the irreflexive equivalence relation with countably many equivalence classes of countable size. Since both structures are transitive and have no algebraicity, the superposition structure has the same properties which are then inherited by
$\mathbb {K}_{2,\omega }$
with the irreflexive equivalence relation with countably many equivalence classes of countable size. Since both structures are transitive and have no algebraicity, the superposition structure has the same properties which are then inherited by
![]() $\mathbb {G}$
since a first-order reduct can only have additional automorphisms.
$\mathbb {G}$
since a first-order reduct can only have additional automorphisms.
To simplify the presentation, we additionally define a few notational shorthands concerning endomorphisms of
![]() $\mathbb {G}$
:
$\mathbb {G}$
:
Notation 4.9.
-
(i) For
 $p=\bigsqcup _{i\in \mathbb {N}}^{\xi }p_{i}\in \operatorname {\mathrm {End}}(\mathbb {G})$
, we define
$p=\bigsqcup _{i\in \mathbb {N}}^{\xi }p_{i}\in \operatorname {\mathrm {End}}(\mathbb {G})$
, we define
 $\tilde {p}:=\xi \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.
$\tilde {p}:=\xi \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
. -
(ii) Given
 $p_{0},\dots ,p_{k}\in \operatorname {\mathrm {End}}(\mathbb {G})$
and
$p_{0},\dots ,p_{k}\in \operatorname {\mathrm {End}}(\mathbb {G})$
and
 $\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
,
$\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
,
 $s\in \operatorname {\mathrm {End}}(\mathbb {G})$
, we define
$s\in \operatorname {\mathrm {End}}(\mathbb {G})$
, we define
 $\tilde {\varphi }(\tau ):=\tilde {p}_{k}\tau \tilde {p}_{k-1}\tau \dots \tau \tilde {p}_{0}$
,
$\tilde {\varphi }(\tau ):=\tilde {p}_{k}\tau \tilde {p}_{k-1}\tau \dots \tau \tilde {p}_{0}$
,
 $\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.
$\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.
4.2 Proof strategy
The goal of Section 4 is to prove the following:
Theorem 4.10. On the endomorphism monoid of the structure
![]() $\mathbb {G}$
, the pointwise topology is strictly finer than the Zariski topology.
$\mathbb {G}$
, the pointwise topology is strictly finer than the Zariski topology.
Remark 4.11. Before we go into the details of the proof, let us remark that the structure
![]() $\mathbb {G}$
needs to have an infinite model-complete core which has algebraicity in order to have a chance of satisfying Theorem 4.10—for otherwise, Theorem 3.2 would apply.
$\mathbb {G}$
needs to have an infinite model-complete core which has algebraicity in order to have a chance of satisfying Theorem 4.10—for otherwise, Theorem 3.2 would apply.
The model-complete core of
![]() $\mathbb {K}_{2,\omega }$
is just the graph consisting of a single edge, as witnessed for instance, by the substructure induced on
$\mathbb {K}_{2,\omega }$
is just the graph consisting of a single edge, as witnessed for instance, by the substructure induced on
![]() $\{a_{+1},a_{-1}\}$
and the homomorphism
$\{a_{+1},a_{-1}\}$
and the homomorphism
![]() $c_{+1}\colon \mathbb {K}_{2,\omega }\to \{a_{+1},a_{-1}\}$
. We claim that the model-complete core of
$c_{+1}\colon \mathbb {K}_{2,\omega }\to \{a_{+1},a_{-1}\}$
. We claim that the model-complete core of
![]() $\mathbb {G}$
is the complete graph on countably many vertices where each point has as fine structure a single edge, i.e., the substructure
$\mathbb {G}$
is the complete graph on countably many vertices where each point has as fine structure a single edge, i.e., the substructure
![]() $\mathbb {C}$
of
$\mathbb {C}$
of
![]() $\mathbb {G}$
induced on
$\mathbb {G}$
induced on
![]() $C:=\mathbb {N}\times \{a_{+1},a_{-1}\}\subseteq G$
(see Figure 2).
$C:=\mathbb {N}\times \{a_{+1},a_{-1}\}\subseteq G$
(see Figure 2).

Figure 2 The model-complete core of
![]() $\mathbb {G}$
: complete graph on countably many vertices (dashed) where each point has a single edge (solid) as fine structure.
$\mathbb {G}$
: complete graph on countably many vertices (dashed) where each point has a single edge (solid) as fine structure.
Similarly to the proof of Lemma 4.5, one easily checks that (here,
![]() $c_{\pm 1}$
are considered as self-maps of
$c_{\pm 1}$
are considered as self-maps of
![]() $\{a_{+1},a_{-1}\}$
)
$\{a_{+1},a_{-1}\}$
)
 $$ \begin{align*} \operatorname{\mathrm{End}}(\mathbb{C})&=\left\{\bigsqcup_{i\in\mathbb{N}}\!^{\tau} \gamma_{i}:\tau\in\operatorname{\mathrm{Inj}}(\mathbb{N}),\gamma_{i}\in\{c_{+1},c_{-1}\}\right\},\\ \operatorname{\mathrm{Aut}}(\mathbb{C})&=\left\{\bigsqcup_{i\in\mathbb{N}}\!^{\sigma} \gamma_{i}:\sigma\in\operatorname{\mathrm{Sym}}(\mathbb{N}),\gamma_{i}\in\{c_{+1},c_{-1}\}\right\}. \end{align*} $$
$$ \begin{align*} \operatorname{\mathrm{End}}(\mathbb{C})&=\left\{\bigsqcup_{i\in\mathbb{N}}\!^{\tau} \gamma_{i}:\tau\in\operatorname{\mathrm{Inj}}(\mathbb{N}),\gamma_{i}\in\{c_{+1},c_{-1}\}\right\},\\ \operatorname{\mathrm{Aut}}(\mathbb{C})&=\left\{\bigsqcup_{i\in\mathbb{N}}\!^{\sigma} \gamma_{i}:\sigma\in\operatorname{\mathrm{Sym}}(\mathbb{N}),\gamma_{i}\in\{c_{+1},c_{-1}\}\right\}. \end{align*} $$
Thus, any endomorphism is locally interpolated by an automorphism, and
![]() $\mathbb {C}$
is indeed a model-complete core. Additionally,
$\mathbb {C}$
is indeed a model-complete core. Additionally,
![]() $\mathbb {G}$
and
$\mathbb {G}$
and
![]() $\mathbb {C}$
are homomorphically equivalent—an example of a homomorphism
$\mathbb {C}$
are homomorphically equivalent—an example of a homomorphism
![]() $\mathbb {G}\to \mathbb {C}$
is given by
$\mathbb {G}\to \mathbb {C}$
is given by
![]() $\bigsqcup _{i\in \mathbb {N}}^{\operatorname {\mathrm {id}}}c_{+1}$
(where
$\bigsqcup _{i\in \mathbb {N}}^{\operatorname {\mathrm {id}}}c_{+1}$
(where
![]() $c_{+1}$
is considered as a map defined on
$c_{+1}$
is considered as a map defined on
![]() $K_{2,\omega }$
).
$K_{2,\omega }$
).
Finally,
![]() $\mathbb {C}$
has algebraicity: any automorphism of
$\mathbb {C}$
has algebraicity: any automorphism of
![]() $\mathbb {C}$
which stabilises
$\mathbb {C}$
which stabilises
![]() $Y:=\{(0,a_{+1})\}$
also stabilises
$Y:=\{(0,a_{+1})\}$
also stabilises
![]() $a:=(0,a_{-1})$
, so the Y-related orbit of a is finite.
$a:=(0,a_{-1})$
, so the Y-related orbit of a is finite.
In order to show Theorem 4.10, we will prove that
![]() $\mathcal {T}_{\text {Zariski}}$
-open sets on
$\mathcal {T}_{\text {Zariski}}$
-open sets on
![]() $\operatorname {\mathrm {End}}(\mathbb {G})$
cannot determine the sign of the components
$\operatorname {\mathrm {End}}(\mathbb {G})$
cannot determine the sign of the components
![]() $s_{i}$
of
$s_{i}$
of
![]() $s=\bigsqcup _{i\in \mathbb {N}}^{\tau }s_{i}$
, in other words decide whether the functions
$s=\bigsqcup _{i\in \mathbb {N}}^{\tau }s_{i}$
, in other words decide whether the functions
![]() $s_{i}$
switch the two parts of
$s_{i}$
switch the two parts of
![]() $\mathbb {K}_{2,\omega }$
or not. On the other hand,
$\mathbb {K}_{2,\omega }$
or not. On the other hand,
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}$
-open sets can determine the sign of finitely many components, thus showing
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}$
-open sets can determine the sign of finitely many components, thus showing
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}\neq \mathcal {T}_{\text {Zariski}}$
. More precisely, we will prove that if a
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}\neq \mathcal {T}_{\text {Zariski}}$
. More precisely, we will prove that if a
![]() $\mathcal {T}_{\text {Zariski}}$
-generating set
$\mathcal {T}_{\text {Zariski}}$
-generating set
![]() $M_{\varphi ,\psi }$
contains
$M_{\varphi ,\psi }$
contains
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
, then it also contains
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
, then it also contains
![]() $\tau \ltimes c_{-1}$
for all elements
$\tau \ltimes c_{-1}$
for all elements
![]() $\tau $
of a “big” subset of
$\tau $
of a “big” subset of
![]() $\operatorname {\mathrm {Inj}}(\mathbb {N})$
—where “big” means either “
$\operatorname {\mathrm {Inj}}(\mathbb {N})$
—where “big” means either “
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
” (if the terms
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
” (if the terms
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
have equal lengths; see Lemmas 4.12 and 4.13) or “
$\psi $
have equal lengths; see Lemmas 4.12 and 4.13) or “
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set” (if the terms
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set” (if the terms
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
have different lengths; see Lemma 4.14).
$\psi $
have different lengths; see Lemma 4.14).
Our (almost trivial) first lemma analogously holds in a more general setting. Since we only apply it in case of terms of equal lengths, we formulate it in the present form.
Lemma 4.12.
-
(i) Let
 $k\geq 1$
and let
$k\geq 1$
and let
 $\xi _{0},\dots ,\xi _{k},\theta _{0},\dots ,\theta _{k}\in \operatorname {\mathrm {Inj}}(\mathbb {N})$
as well as
$\xi _{0},\dots ,\xi _{k},\theta _{0},\dots ,\theta _{k}\in \operatorname {\mathrm {Inj}}(\mathbb {N})$
as well as
 $\tilde {\varphi }(\tau ):=\xi _{k}\tau \xi _{k-1}\tau \dots \tau \xi _{0}$
and
$\tilde {\varphi }(\tau ):=\xi _{k}\tau \xi _{k-1}\tau \dots \tau \xi _{0}$
and
 $\tilde {\psi }(\tau ):=\theta _{k}\tau \theta _{k-1}\tau \dots \tau \theta _{0}$
,
$\tilde {\psi }(\tau ):=\theta _{k}\tau \theta _{k-1}\tau \dots \tau \theta _{0}$
,
 $\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.
$\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.If
 $\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})\neq \tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
, then
$\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})\neq \tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
, then
 $M_{\tilde {\varphi },\tilde {\psi }}=\left \{\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}):\tilde {\varphi }(\tau )\neq \tilde {\psi }(\tau )\right \}$
is a
$M_{\tilde {\varphi },\tilde {\psi }}=\left \{\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}):\tilde {\varphi }(\tau )\neq \tilde {\psi }(\tau )\right \}$
is a
 $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
 $\operatorname {\mathrm {id}}_{\mathbb {N}}$
.
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
. -
(ii) Let
 $k\geq 1$
and let
$k\geq 1$
and let
 $p_{0},\dots ,p_{k},q_{0},\dots ,q_{k}\in \operatorname {\mathrm {End}}(\mathbb {G})$
as well as
$p_{0},\dots ,p_{k},q_{0},\dots ,q_{k}\in \operatorname {\mathrm {End}}(\mathbb {G})$
as well as
 $\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
$\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
 $\psi (s):=q_{k}sq_{k-1}s\dots sq_{0}$
,
$\psi (s):=q_{k}sq_{k-1}s\dots sq_{0}$
,
 $s\in \operatorname {\mathrm {End}}(\mathbb {G})$
. Assume
$s\in \operatorname {\mathrm {End}}(\mathbb {G})$
. Assume
 $\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})\neq \tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
(using the shorthand from Notation 4.9).
$\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})\neq \tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
(using the shorthand from Notation 4.9).Then there exists a
 $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood U of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood U of
 $\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
 $\tau \ltimes t\in M_{\varphi ,\psi }=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):\varphi (s)\neq \psi (s)\right \}$
for all
$\tau \ltimes t\in M_{\varphi ,\psi }=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):\varphi (s)\neq \psi (s)\right \}$
for all
 $\tau \in U$
and
$\tau \in U$
and
 $t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
. In particular,
$t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
. In particular,
 $\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
for all
$\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
for all
 $\tau \in U$
.
$\tau \in U$
.
The second lemma really requires the terms to be of equal length.
Lemma 4.13. Let
![]() $k\geq 1$
and let
$k\geq 1$
and let
![]() $p_{0},\dots ,p_{k},q_{0},\dots ,q_{k}\in \operatorname {\mathrm {End}}(\mathbb {G})$
as well as
$p_{0},\dots ,p_{k},q_{0},\dots ,q_{k}\in \operatorname {\mathrm {End}}(\mathbb {G})$
as well as
![]() $\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
$\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
![]() $\psi (s):=q_{k}sq_{k-1}s\dots sq_{0}$
,
$\psi (s):=q_{k}sq_{k-1}s\dots sq_{0}$
,
![]() $s\in \operatorname {\mathrm {End}}(\mathbb {G})$
. Assume
$s\in \operatorname {\mathrm {End}}(\mathbb {G})$
. Assume
![]() $\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})\neq \psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})$
but
$\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})\neq \psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})$
but
![]() $\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})=\tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
.
$\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})=\tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
.
Then there exists a
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood U of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood U of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
![]() $\tau \ltimes c_{-1}\in M_{\varphi ,\psi }=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):\varphi (s)\neq \psi (s)\right \}$
for all
$\tau \ltimes c_{-1}\in M_{\varphi ,\psi }=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):\varphi (s)\neq \psi (s)\right \}$
for all
![]() $\tau \in U$
.
$\tau \in U$
.
Finally, we formulate a result for terms of different lengths.
Lemma 4.14.
-
(i) Let
 $\ell <k$
and let
$\ell <k$
and let
 $\xi _{0},\dots ,\xi _{k},\theta _{0},\dots ,\theta _{\ell }\in \operatorname {\mathrm {Inj}}(\mathbb {N})$
as well as
$\xi _{0},\dots ,\xi _{k},\theta _{0},\dots ,\theta _{\ell }\in \operatorname {\mathrm {Inj}}(\mathbb {N})$
as well as
 $\tilde {\varphi }(\tau ):=\xi _{k}\tau \xi _{k-1}\tau \dots \tau \xi _{0}$
and
$\tilde {\varphi }(\tau ):=\xi _{k}\tau \xi _{k-1}\tau \dots \tau \xi _{0}$
and
 $\tilde {\psi }(\tau ):=\theta _{\ell }\tau \theta _{\ell -1}\tau \dots \tau \theta _{0}$
,
$\tilde {\psi }(\tau ):=\theta _{\ell }\tau \theta _{\ell -1}\tau \dots \tau \theta _{0}$
,
 $\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.
$\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
.Then
 $M_{\tilde {\varphi },\tilde {\psi }}=\left \{\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}):\tilde {\varphi } (\tau )\neq \tilde {\psi }(\tau )\right \}$
is
$M_{\tilde {\varphi },\tilde {\psi }}=\left \{\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}):\tilde {\varphi } (\tau )\neq \tilde {\psi }(\tau )\right \}$
is
 $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open.
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open. -
(ii) Let
 $\ell <k$
and let
$\ell <k$
and let
 $p_{0},\dots ,p_{k},q_{0},\dots ,q_{\ell }\in \operatorname {\mathrm {End}}(\mathbb {G})$
as well as
$p_{0},\dots ,p_{k},q_{0},\dots ,q_{\ell }\in \operatorname {\mathrm {End}}(\mathbb {G})$
as well as
 $\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
$\varphi (s):=p_{k}sp_{k-1}s\dots sp_{0}$
and
 $\psi (s):=q_{\ell }sq_{\ell -1}s\dots sq_{0}$
,
$\psi (s):=q_{\ell }sq_{\ell -1}s\dots sq_{0}$
,
 $s\in \operatorname {\mathrm {End}}(\mathbb {G})$
.
$s\in \operatorname {\mathrm {End}}(\mathbb {G})$
.Then there exists a
 $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set V such that
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set V such that
 $\tau \ltimes t\in M_{\varphi ,\psi }=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):\varphi (s)\neq \psi (s)\right \}$
for all
$\tau \ltimes t\in M_{\varphi ,\psi }=\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):\varphi (s)\neq \psi (s)\right \}$
for all
 $\tau \in V$
and
$\tau \in V$
and
 $t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
. In particular,
$t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
. In particular,
 $\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
for all
$\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
for all
 $\tau \in V$
.
$\tau \in V$
.
We first demonstrate how these auxiliary statements are used and prove Theorem 4.10 before showing the statements themselves in Section 4.3.
Proof (of Theorem 4.10 given Lemmas 4.12–4.14)
We will show that any
![]() $\mathcal {T}_{\text {Zariski}}$
-open set O containing
$\mathcal {T}_{\text {Zariski}}$
-open set O containing
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
also contains
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
also contains
![]() $\tau \ltimes c_{-1}$
for some
$\tau \ltimes c_{-1}$
for some
![]() $\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
. This implies in particular that the
$\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
. This implies in particular that the
![]() $\mathcal {T}_{pw}$
-open set
$\mathcal {T}_{pw}$
-open set
![]() $\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):s(0,a_{+1})=(0,a_{+1})\right \}$
cannot be
$\left \{s\in \operatorname {\mathrm {End}}(\mathbb {G}):s(0,a_{+1})=(0,a_{+1})\right \}$
cannot be
![]() $\mathcal {T}_{\text {Zariski}}$
-open—proving
$\mathcal {T}_{\text {Zariski}}$
-open—proving
![]() $\mathcal {T}_{\text {Zariski}}\neq \mathcal {T}_{pw}$
.
$\mathcal {T}_{\text {Zariski}}\neq \mathcal {T}_{pw}$
.
It suffices to consider
![]() $\mathcal {T}_{\text {Zariski}}$
-basic open sets O, i.e.,
$\mathcal {T}_{\text {Zariski}}$
-basic open sets O, i.e.,
![]() $O=\bigcap _{h\in H}M_{\varphi _{h},\psi _{h}}\ni \operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
for some finite set H. If the terms
$O=\bigcap _{h\in H}M_{\varphi _{h},\psi _{h}}\ni \operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
for some finite set H. If the terms
![]() $\varphi _{h}$
and
$\varphi _{h}$
and
![]() $\psi _{h}$
have equal length, we apply Lemma 4.12 or 4.13 to find a
$\psi _{h}$
have equal length, we apply Lemma 4.12 or 4.13 to find a
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood
![]() $U_{h}$
of
$U_{h}$
of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
![]() $\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
$\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
![]() $\tau \in U_{h}$
. If
$\tau \in U_{h}$
. If
![]() $\varphi _{h}$
and
$\varphi _{h}$
and
![]() $\psi _{h}$
have different lengths, we instead applyFootnote
3
Lemma 4.14 to find a
$\psi _{h}$
have different lengths, we instead applyFootnote
3
Lemma 4.14 to find a
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set
![]() $V_{h}$
such that
$V_{h}$
such that
![]() $\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
$\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
![]() $\tau \in V_{h}$
. Intersecting the respective sets
$\tau \in V_{h}$
. Intersecting the respective sets
![]() $U_{h}$
and
$U_{h}$
and
![]() $V_{h}$
thus obtained yields a
$V_{h}$
thus obtained yields a
![]() $\mathcal {T}_{pw}$
-open neighbourhood U of
$\mathcal {T}_{pw}$
-open neighbourhood U of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
and a
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
and a
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set V such that
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense and open set V such that
![]() $\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
$\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
![]() $\tau \in U$
whenever
$\tau \in U$
whenever
![]() $\varphi _{h}$
and
$\varphi _{h}$
and
![]() $\psi _{h}$
have equal length and such that
$\psi _{h}$
have equal length and such that
![]() $\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
$\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
![]() $\tau \in V$
whenever
$\tau \in V$
whenever
![]() $\varphi _{h}$
and
$\varphi _{h}$
and
![]() $\psi _{h}$
have different lengths. The intersection
$\psi _{h}$
have different lengths. The intersection
![]() $U\cap V$
is nonempty; for any
$U\cap V$
is nonempty; for any
![]() $\tau \in U\cap V$
we have
$\tau \in U\cap V$
we have
![]() $\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
$\tau \ltimes c_{-1}\in M_{\varphi _{h},\psi _{h}}$
for all
![]() $h\in H$
, i.e.,
$h\in H$
, i.e.,
![]() $\tau \ltimes c_{-1}\in O$
. This concludes the proof.
$\tau \ltimes c_{-1}\in O$
. This concludes the proof.
Remark 4.15. A slight refinement of this proof even shows that the Zariski topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {G})$
is not Hausdorff since
$\operatorname {\mathrm {End}}(\mathbb {G})$
is not Hausdorff since
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
and
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
and
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}$
cannot be separated by open sets: By the proof, a given basic open set around
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}$
cannot be separated by open sets: By the proof, a given basic open set around
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
contains
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
contains
![]() $\tau \ltimes c_{-1}$
provided that
$\tau \ltimes c_{-1}$
provided that
![]() $\tau $
is an element of the intersection of a certain
$\tau $
is an element of the intersection of a certain
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
and a
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
and a
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense open set. The same idea similarly (but with an easier proof in the analogue of Lemma 4.13) yields that a given basic open set around
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense open set. The same idea similarly (but with an easier proof in the analogue of Lemma 4.13) yields that a given basic open set around
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}$
contains
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}$
contains
![]() $\tau '\ltimes c_{-1}$
provided that
$\tau '\ltimes c_{-1}$
provided that
![]() $\tau '$
is an element of the intersection of another
$\tau '$
is an element of the intersection of another
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
and another
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
and another
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense open set. The intersection of these four sets is nonempty, so the basic open sets around
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense open set. The intersection of these four sets is nonempty, so the basic open sets around
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
and
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1}$
and
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}$
contain a common element (namely
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}$
contain a common element (namely
![]() $\tau \ltimes c_{-1}$
for a certain
$\tau \ltimes c_{-1}$
for a certain
![]() $\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
).
$\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
).
The preceding remark suggests the following refinement of Question 1.1:
Question 4.1. Is there an
![]() $\omega $
-categorical (transitive?) relational structure
$\omega $
-categorical (transitive?) relational structure
![]() $\mathbb {A}$
such that there exists a Hausdorff (even Polish?) semigroup topology on
$\mathbb {A}$
such that there exists a Hausdorff (even Polish?) semigroup topology on
![]() $\operatorname {\mathrm {End}}(\mathbb {A})$
which is not finer than the topology of pointwise convergence?
$\operatorname {\mathrm {End}}(\mathbb {A})$
which is not finer than the topology of pointwise convergence?
4.3 Proof details
In this subsection, we prove Lemmas 4.12–4.14 in sequence.
Proof (of Lemma 4.12)
(i) The set
![]() $M_{\tilde {\varphi },\tilde {\psi }}\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})$
is open with respect to
$M_{\tilde {\varphi },\tilde {\psi }}\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})$
is open with respect to
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
since
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
since
![]() $\tilde {\varphi }$
and
$\tilde {\varphi }$
and
![]() $\tilde {\psi }$
are continuous with respect to
$\tilde {\psi }$
are continuous with respect to
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
.
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
.
(ii) Set
![]() $U:=M_{\tilde {\varphi },\tilde {\psi }}$
and note that if
$U:=M_{\tilde {\varphi },\tilde {\psi }}$
and note that if
![]() $u:=\varphi (\tau \ltimes t)$
and
$u:=\varphi (\tau \ltimes t)$
and
![]() $v:=\psi (\tau \ltimes t)$
, then
$v:=\psi (\tau \ltimes t)$
, then
![]() ${\tilde {u}=\tilde {\varphi }(\tau )\neq \tilde {\psi }(\tau )=\tilde {v}}$
, so
${\tilde {u}=\tilde {\varphi }(\tau )\neq \tilde {\psi }(\tau )=\tilde {v}}$
, so
![]() $u\neq v$
.
$u\neq v$
.
The second lemma requires more work.
Proof (of Lemma 4.13)
We start by fixing some notation. We first write
![]() ${p_{j}=\bigsqcup _{i\in \mathbb {N}}^{\xi _{j}}p_{j,i}}$
,
${p_{j}=\bigsqcup _{i\in \mathbb {N}}^{\xi _{j}}p_{j,i}}$
,
![]() $q_{j}=\bigsqcup _{i\in \mathbb {N}}^{\theta _{j}}q_{j,i}$
(so
$q_{j}=\bigsqcup _{i\in \mathbb {N}}^{\theta _{j}}q_{j,i}$
(so
![]() $\xi _{j}=\tilde {p}_{j}$
,
$\xi _{j}=\tilde {p}_{j}$
,
![]() $\theta _{j}=\tilde {q}_{j}$
), and
$\theta _{j}=\tilde {q}_{j}$
), and
![]() $\delta :=\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})=\tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
. Further, we define
$\delta :=\tilde {\varphi }(\operatorname {\mathrm {id}}_{\mathbb {N}})=\tilde {\psi }(\operatorname {\mathrm {id}}_{\mathbb {N}})$
. Further, we define
![]() $\Xi _{j}:=\xi _{j}\xi _{j-1}\dots \xi _{0}$
as well as
$\Xi _{j}:=\xi _{j}\xi _{j-1}\dots \xi _{0}$
as well as
![]() $\Theta _{j}:=\theta _{j}\theta _{j-1}\dots \theta _{0}$
,
$\Theta _{j}:=\theta _{j}\theta _{j-1}\dots \theta _{0}$
,
![]() $j=0,\dots ,k$
. In particular,
$j=0,\dots ,k$
. In particular,
![]() $\Xi _{k}=\Theta _{k}=\delta $
. Let the two (distinct, by assumption) functions
$\Xi _{k}=\Theta _{k}=\delta $
. Let the two (distinct, by assumption) functions
![]() $\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})$
and
$\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})$
and
![]() $\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})$
differ at the point
$\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})$
differ at the point
![]() $(h,x)\in G$
. Further, set
$(h,x)\in G$
. Further, set
![]() ${e\in \{-1,+1\}}$
such that
${e\in \{-1,+1\}}$
such that
![]() $x\in A_{e}$
and choose any
$x\in A_{e}$
and choose any
![]() $x'\in A_{-e}$
.
$x'\in A_{-e}$
.
In the course of the proof, we will require the explicit expansions of the compositions in
![]() $\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
and
$\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
and
![]() $\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
:
$\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
:
 $$ \begin{align*} \varphi(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{\pm 1})&=\bigsqcup_{i\in\mathbb{N}}\!^{\delta}p_{k,\Xi_{k-1}(i)}c_{\pm 1}p_{k-1,\Xi_{k-2}(i)}\dots c_{\pm 1}p_{0,i},\\ \psi(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{\pm 1})&=\bigsqcup_{i\in\mathbb{N}}\!^{\delta}q_{k,\Theta_{k-1}(i)}c_{\pm 1}q_{k-1,\Theta_{k-2}(i)}\dots c_{\pm 1}q_{0,i}. \end{align*} $$
$$ \begin{align*} \varphi(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{\pm 1})&=\bigsqcup_{i\in\mathbb{N}}\!^{\delta}p_{k,\Xi_{k-1}(i)}c_{\pm 1}p_{k-1,\Xi_{k-2}(i)}\dots c_{\pm 1}p_{0,i},\\ \psi(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{\pm 1})&=\bigsqcup_{i\in\mathbb{N}}\!^{\delta}q_{k,\Theta_{k-1}(i)}c_{\pm 1}q_{k-1,\Theta_{k-2}(i)}\dots c_{\pm 1}q_{0,i}. \end{align*} $$
We proceed in two steps—first, we show that
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
; second, we extend this to
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
; second, we extend this to
![]() $\tau \ltimes c_{-1}$
for all
$\tau \ltimes c_{-1}$
for all
![]() $\tau $
in an appropriately constructed
$\tau $
in an appropriately constructed
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
.
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
.
(1)
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
: We compare
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
: We compare
![]() $\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
and
$\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
and
![]() $\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
at
$\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{\pm 1})$
at
![]() $(h,x)$
as well as
$(h,x)$
as well as
![]() $(h,x')$
. In order to simplify notation, we defineFootnote
4
$(h,x')$
. In order to simplify notation, we defineFootnote
4
 $$ \begin{align*} m&:=\operatorname{\mathrm{sgn}}(p_{k-1,\Xi_{k-2}(h)})\cdot\operatorname{\mathrm{sgn}}(p_{k-2,\Xi_{k-3}(h)})\cdot\ldots\cdot\operatorname{\mathrm{sgn}}(p_{0,h}),\\ n&:=\operatorname{\mathrm{sgn}}(q_{k-1,\Theta_{k-2}(h)})\cdot\operatorname{\mathrm{sgn}}(q_{k-2,\Theta_{k-3}(h)})\cdot\ldots\cdot\operatorname{\mathrm{sgn}}(q_{0,h}),\\ \widehat{p}&:=p_{k,\Xi_{k-1}(h)},\\ \widehat{q}&:=q_{k,\Xi_{k-1}(h)}, \end{align*} $$
$$ \begin{align*} m&:=\operatorname{\mathrm{sgn}}(p_{k-1,\Xi_{k-2}(h)})\cdot\operatorname{\mathrm{sgn}}(p_{k-2,\Xi_{k-3}(h)})\cdot\ldots\cdot\operatorname{\mathrm{sgn}}(p_{0,h}),\\ n&:=\operatorname{\mathrm{sgn}}(q_{k-1,\Theta_{k-2}(h)})\cdot\operatorname{\mathrm{sgn}}(q_{k-2,\Theta_{k-3}(h)})\cdot\ldots\cdot\operatorname{\mathrm{sgn}}(q_{0,h}),\\ \widehat{p}&:=p_{k,\Xi_{k-1}(h)},\\ \widehat{q}&:=q_{k,\Xi_{k-1}(h)}, \end{align*} $$
and conclude
 $$ \begin{align*} [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x) & =\Big(\delta(h),\widehat{p}(a_{me})\Big), & [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x) & =\Big(\delta(h),\widehat{p}(a_{me(-1)^{k}})\Big),\\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x)&=\Big(\delta(h),\widehat{q}(a_{ne})\Big),&\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x)&=\Big(\delta(h),\widehat{q}(a_{ne(-1)^{k}})\Big),\\ [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x')&=\Big(\delta(h),\widehat{p}(a_{-me})\Big),&\ [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x')&=\Big(\delta(h),\widehat{p}(a_{-me(-1)^{k}})\Big),\\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x')&=\Big(\delta(h),\widehat{q}(a_{-ne})\Big),&\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x')&=\Big(\delta(h),\widehat{q}(a_{-ne(-1)^{k}})\Big). \end{align*} $$
$$ \begin{align*} [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x) & =\Big(\delta(h),\widehat{p}(a_{me})\Big), & [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x) & =\Big(\delta(h),\widehat{p}(a_{me(-1)^{k}})\Big),\\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x)&=\Big(\delta(h),\widehat{q}(a_{ne})\Big),&\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x)&=\Big(\delta(h),\widehat{q}(a_{ne(-1)^{k}})\Big),\\ [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x')&=\Big(\delta(h),\widehat{p}(a_{-me})\Big),&\ [\varphi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x')&=\Big(\delta(h),\widehat{p}(a_{-me(-1)^{k}})\Big),\\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{+1}\right)](h,x')&=\Big(\delta(h),\widehat{q}(a_{-ne})\Big),&\ [\psi\left(\operatorname{\mathrm{id}}_{\mathbb{N}}\ltimes c_{-1}\right)](h,x')&=\Big(\delta(h),\widehat{q}(a_{-ne(-1)^{k}})\Big). \end{align*} $$
If
then
![]() $\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})$
and
$\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})$
and
![]() $\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})$
cannot coincide on both
$\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})$
cannot coincide on both
![]() $(h,x)$
and
$(h,x)$
and
![]() $(h,x')$
, so
$(h,x')$
, so
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
as claimed.
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
as claimed.
In case of
we distinguish further: If
![]() $m=n$
, then
$m=n$
, then
![]() $[\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})](h,x)\neq [\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})](h,x)$
shows
$[\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})](h,x)\neq [\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{+1})](h,x)$
shows
which leads toFootnote
5
![]() $[\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)\neq [\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)$
, so
$[\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)\neq [\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)$
, so
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
as claimed. If on the other hand
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
as claimed. If on the other hand
![]() $m=-n$
, then we analogously obtain
$m=-n$
, then we analogously obtain
and
![]() $[\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)\neq [\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)$
, so
$[\varphi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)\neq [\psi (\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1})](h,x)$
, so
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
as claimed.
$\operatorname {\mathrm {id}}_{\mathbb {N}}\ltimes c_{-1}\in M_{\varphi ,\psi }$
as claimed.
(2) There exists a
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open neighbourhood
![]() $U\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})$
of
$U\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})$
of
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
such that
![]() $\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
for all
$\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
for all
![]() $\tau \in U$
: One immediately checks that for arbitrary
$\tau \in U$
: One immediately checks that for arbitrary
![]() $t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
, the map
$t\in \operatorname {\mathrm {End}}(\mathbb {K}_{2,\omega })$
, the map
![]() $\chi _{t}\colon \operatorname {\mathrm {Inj}}(\mathbb {N})\to \operatorname {\mathrm {End}}(\mathbb {G})$
,
$\chi _{t}\colon \operatorname {\mathrm {Inj}}(\mathbb {N})\to \operatorname {\mathrm {End}}(\mathbb {G})$
,
![]() $\chi _{t}(\tau ):=\tau \ltimes t$
is continuous with respect to
$\chi _{t}(\tau ):=\tau \ltimes t$
is continuous with respect to
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
andFootnote
6
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
andFootnote
6
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}$
. Since
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}$
. Since
![]() $M_{\varphi ,\psi }$
is open with respect to
$M_{\varphi ,\psi }$
is open with respect to
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}$
, the preimage
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {End}}(\mathbb {G})}$
, the preimage
![]() ${U:=\chi _{c_{-1}}^{-1}(M_{\varphi ,\psi })\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})}$
is open with respect to
${U:=\chi _{c_{-1}}^{-1}(M_{\varphi ,\psi })\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})}$
is open with respect to
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
. By (1), the set U contains
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
. By (1), the set U contains
![]() $\operatorname {\mathrm {id}}_{\mathbb {N}}$
—completing the proof.
$\operatorname {\mathrm {id}}_{\mathbb {N}}$
—completing the proof.
Finally, we show the third lemma.
Proof (of Lemma 4.14)
(i) We have to prove that for two tuples
![]() $\bar {z},\bar {w}$
of the same length such that
$\bar {z},\bar {w}$
of the same length such that
![]() $\bar {w}$
does not contain the same value twice (since we are working in
$\bar {w}$
does not contain the same value twice (since we are working in
![]() $\operatorname {\mathrm {Inj}}(\mathbb {N})$
), the intersection
$\operatorname {\mathrm {Inj}}(\mathbb {N})$
), the intersection
![]() $\left \{\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}):\tau (\bar {z})=\bar {w}\right \}\cap M_{\tilde {\varphi },\tilde {\psi }}$
is nonempty. The idea behind the proof is to find an element
$\left \{\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N}):\tau (\bar {z})=\bar {w}\right \}\cap M_{\tilde {\varphi },\tilde {\psi }}$
is nonempty. The idea behind the proof is to find an element
![]() $x_{0}\in \mathbb {N}$
and inductively construct a partial injection
$x_{0}\in \mathbb {N}$
and inductively construct a partial injection
![]() $\widehat {\tau }$
which extends
$\widehat {\tau }$
which extends
![]() $\bar {z}\mapsto \bar {w}$
such that the values
$\bar {z}\mapsto \bar {w}$
such that the values
are welldefined (i.e.,
![]() $\xi _{0}(x_{0})\in \operatorname {\mathrm {Dom}}(\widehat {\tau })$
,
$\xi _{0}(x_{0})\in \operatorname {\mathrm {Dom}}(\widehat {\tau })$
,
![]() $\xi _{1}\widehat {\tau }\xi _{0}(x_{0})\in \operatorname {\mathrm {Dom}}(\widehat {\tau })$
, etc.) and
$\xi _{1}\widehat {\tau }\xi _{0}(x_{0})\in \operatorname {\mathrm {Dom}}(\widehat {\tau })$
, etc.) and
![]() $[\tilde {\varphi }(\widehat {\tau })](x_{0})\neq [\tilde {\psi }(\widehat {\tau })](x_{0})$
. This gives
$[\tilde {\varphi }(\widehat {\tau })](x_{0})\neq [\tilde {\psi }(\widehat {\tau })](x_{0})$
. This gives
![]() $\tau (\bar {z})=\bar {w}$
and
$\tau (\bar {z})=\bar {w}$
and
![]() $\tau \in M_{\tilde {\varphi },\tilde {\psi }}$
for any
$\tau \in M_{\tilde {\varphi },\tilde {\psi }}$
for any
![]() $\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
extending
$\tau \in \operatorname {\mathrm {Inj}}(\mathbb {N})$
extending
![]() $\widehat {\tau }$
.
$\widehat {\tau }$
.
More precisely, we will define (not necessarily distinct) elements
![]() $x_{0},\dots ,x_{k}, x^{\prime }_{0},\dots ,x^{\prime }_{k}\in \mathbb {N}$
and
$x_{0},\dots ,x_{k}, x^{\prime }_{0},\dots ,x^{\prime }_{k}\in \mathbb {N}$
and
![]() $y_{0}\dots ,y_{\ell },y^{\prime }_{0},\dots ,y^{\prime }_{\ell }\in \mathbb {N}$
such that:
$y_{0}\dots ,y_{\ell },y^{\prime }_{0},\dots ,y^{\prime }_{\ell }\in \mathbb {N}$
such that:
-
(1)
 $x_{0}=y_{0}$
.
$x_{0}=y_{0}$
. -
(2)
 $x^{\prime }_{j}=\xi _{j}(x_{j})$
for all
$x^{\prime }_{j}=\xi _{j}(x_{j})$
for all
 $j=0,\dots ,k$
.
$j=0,\dots ,k$
. -
(3)
 $y^{\prime }_{j}=\theta _{j}(y_{j})$
for all
$y^{\prime }_{j}=\theta _{j}(y_{j})$
for all
 $j=0,\dots ,\ell $
.
$j=0,\dots ,\ell $
. -
(4)
 $\widehat {\tau }$
defined by
$\widehat {\tau }$
defined by
 $\bar {z}\mapsto \bar {w}$
,
$\bar {z}\mapsto \bar {w}$
,
 $(x^{\prime }_{0},\dots ,x^{\prime }_{k-1})\mapsto (x_{1},\dots ,x_{k})$
,
$(x^{\prime }_{0},\dots ,x^{\prime }_{k-1})\mapsto (x_{1},\dots ,x_{k})$
,
 $(y^{\prime }_{0},\dots ,y^{\prime }_{\ell -1})\mapsto (y_{1},\dots ,y_{\ell })$
is a welldefinedFootnote
7
partial injection.
$(y^{\prime }_{0},\dots ,y^{\prime }_{\ell -1})\mapsto (y_{1},\dots ,y_{\ell })$
is a welldefinedFootnote
7
partial injection. -
(5)
 $x^{\prime }_{k}\neq y^{\prime }_{\ell }$
. (This will crucially depend on the assumption
$x^{\prime }_{k}\neq y^{\prime }_{\ell }$
. (This will crucially depend on the assumption
 $\ell <k$
.)
$\ell <k$
.)
We first pick
![]() $x_{0}=y_{0}\in \mathbb {N}$
such that
$x_{0}=y_{0}\in \mathbb {N}$
such that
![]() $x^{\prime }_{0}:=\xi _{0}(x_{0})\notin \bar {z}$
and
$x^{\prime }_{0}:=\xi _{0}(x_{0})\notin \bar {z}$
and
![]() $y^{\prime }_{0}:=\theta _{0}(y_{0})\notin \bar {z}$
; this is possible since the set
$y^{\prime }_{0}:=\theta _{0}(y_{0})\notin \bar {z}$
; this is possible since the set
![]() $\xi _{0}^{-1}(\bar {z})\cup \theta _{0}^{-1}(\bar {w})$
of forbidden points is finite by injectivity of
$\xi _{0}^{-1}(\bar {z})\cup \theta _{0}^{-1}(\bar {w})$
of forbidden points is finite by injectivity of
![]() $\xi _{0}$
and
$\xi _{0}$
and
![]() $\theta _{0}$
. Note that
$\theta _{0}$
. Note that
![]() $x^{\prime }_{0}$
and
$x^{\prime }_{0}$
and
![]() $y^{\prime }_{0}$
are not necessarily different (in particular,
$y^{\prime }_{0}$
are not necessarily different (in particular,
![]() $\xi _{0}=\theta _{0}$
is possible).
$\xi _{0}=\theta _{0}$
is possible).
Suppose that
![]() $1\leq i\leq \ell $
and that
$1\leq i\leq \ell $
and that
![]() $x_{0},\dots ,x_{i-1},x^{\prime }_{0},\dots ,x^{\prime }_{i-1}$
as well as
$x_{0},\dots ,x_{i-1},x^{\prime }_{0},\dots ,x^{\prime }_{i-1}$
as well as
![]() $y_{0},\dots ,y_{i-1}, y^{\prime }_{0},\dots ,y^{\prime }_{i-1}$
are already defined such that (1)–(4) hold (with
$y_{0},\dots ,y_{i-1}, y^{\prime }_{0},\dots ,y^{\prime }_{i-1}$
are already defined such that (1)–(4) hold (with
![]() $i-1$
in place of both k and
$i-1$
in place of both k and
![]() $\ell $
). We abbreviate
$\ell $
). We abbreviate
![]() $X_{i-1}:=\{x_{0},\dots ,x_{i-1}\},X^{\prime }_{i-1}:=\{x^{\prime }_{0},\dots ,x^{\prime }_{i-1}\}$
and
$X_{i-1}:=\{x_{0},\dots ,x_{i-1}\},X^{\prime }_{i-1}:=\{x^{\prime }_{0},\dots ,x^{\prime }_{i-1}\}$
and
![]() $Y_{i-1}:=\{y_{0},\dots ,y_{i-1}\},Y^{\prime }_{i-1}:=\{y^{\prime }_{0},\dots ,y^{\prime }_{i-1}\}$
. Pick
$Y_{i-1}:=\{y_{0},\dots ,y_{i-1}\},Y^{\prime }_{i-1}:=\{y^{\prime }_{0},\dots ,y^{\prime }_{i-1}\}$
. Pick
![]() $x_{i},y_{i}\notin \bar {w}\cup X_{i-1}\cup Y_{i-1}$
such that
$x_{i},y_{i}\notin \bar {w}\cup X_{i-1}\cup Y_{i-1}$
such that
![]() $x^{\prime }_{i}:=\xi _{i}(x_{i})\notin \bar {z}\cup X^{\prime }_{i-1}\cup Y^{\prime }_{i-1}$
and
$x^{\prime }_{i}:=\xi _{i}(x_{i})\notin \bar {z}\cup X^{\prime }_{i-1}\cup Y^{\prime }_{i-1}$
and
![]() $y^{\prime }_{i}:=\theta _{i}(y_{i})\notin \bar {z}\cup X^{\prime }_{i-1}\cup Y^{\prime }_{i-1}$
with the additional property thatFootnote
8
$y^{\prime }_{i}:=\theta _{i}(y_{i})\notin \bar {z}\cup X^{\prime }_{i-1}\cup Y^{\prime }_{i-1}$
with the additional property thatFootnote
8
![]() $x_{i}$
and
$x_{i}$
and
![]() $y_{i}$
are chosen to be distinct if and only if
$y_{i}$
are chosen to be distinct if and only if
![]() $x^{\prime }_{i-1}$
and
$x^{\prime }_{i-1}$
and
![]() $y^{\prime }_{i-1}$
are distinct (to obtain a welldefined partial injection in (4)). As with the construction of
$y^{\prime }_{i-1}$
are distinct (to obtain a welldefined partial injection in (4)). As with the construction of
![]() $x_{0}$
above, this is possible by finiteness of the forbidden sets.
$x_{0}$
above, this is possible by finiteness of the forbidden sets.
If
![]() $\ell +1\leq i\leq k$
and if
$\ell +1\leq i\leq k$
and if
![]() $x_{0},\dots ,x_{i-1},x^{\prime }_{0},\dots ,x^{\prime }_{i-1}$
as well as
$x_{0},\dots ,x_{i-1},x^{\prime }_{0},\dots ,x^{\prime }_{i-1}$
as well as
![]() $y_{0},\dots ,y_{\ell },y^{\prime }_{0},\dots ,y^{\prime }_{\ell }$
are already defined such that (1)–(4) hold (with
$y_{0},\dots ,y_{\ell },y^{\prime }_{0},\dots ,y^{\prime }_{\ell }$
are already defined such that (1)–(4) hold (with
![]() $i-1$
in place of k), then we again abbreviate
$i-1$
in place of k), then we again abbreviate
![]() $X_{i-1}:=\{x_{0},\dots ,x_{i-1}\},X^{\prime }_{i-1}:=\{x^{\prime }_{0},\dots ,x^{\prime }_{i-1}\}$
and
$X_{i-1}:=\{x_{0},\dots ,x_{i-1}\},X^{\prime }_{i-1}:=\{x^{\prime }_{0},\dots ,x^{\prime }_{i-1}\}$
and
![]() $Y_{\ell }:=\{y_{0},\dots ,y_{\ell }\}, Y^{\prime }_{\ell }:=\{y^{\prime }_{0},\dots ,y^{\prime }_{\ell }\}$
. Analogously to the previous step, we pick
$Y_{\ell }:=\{y_{0},\dots ,y_{\ell }\}, Y^{\prime }_{\ell }:=\{y^{\prime }_{0},\dots ,y^{\prime }_{\ell }\}$
. Analogously to the previous step, we pick
![]() $x_{i}\notin \bar {w}\cup X_{i-1}\cup Y_{\ell }$
such that
$x_{i}\notin \bar {w}\cup X_{i-1}\cup Y_{\ell }$
such that
![]() $x^{\prime }_{i}:=\xi _{i}(x_{i})\notin \bar {z}\cup X^{\prime }_{i-1}\cup Y^{\prime }_{\ell }$
. Note that in the final step
$x^{\prime }_{i}:=\xi _{i}(x_{i})\notin \bar {z}\cup X^{\prime }_{i-1}\cup Y^{\prime }_{\ell }$
. Note that in the final step
![]() $i=k$
, we are picking
$i=k$
, we are picking
![]() $x_{k}$
such thatFootnote
9
$x_{k}$
such thatFootnote
9
![]() $x^{\prime }_{k}\notin \bar {z}\cup X^{\prime }_{k-1}\cup Y^{\prime }_{\ell }$
. In particular, we require
$x^{\prime }_{k}\notin \bar {z}\cup X^{\prime }_{k-1}\cup Y^{\prime }_{\ell }$
. In particular, we require
![]() $x^{\prime }_{k}\neq y^{\prime }_{\ell }$
, i.e., (5).
$x^{\prime }_{k}\neq y^{\prime }_{\ell }$
, i.e., (5).
(ii) The set
![]() $V:=M_{\tilde {\varphi },\tilde {\psi }}\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})$
is
$V:=M_{\tilde {\varphi },\tilde {\psi }}\subseteq \operatorname {\mathrm {Inj}}(\mathbb {N})$
is
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense by the first statement and clearly
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-dense by the first statement and clearly
![]() $\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open. For
$\mathcal {T}_{pw}\vert _{\operatorname {\mathrm {Inj}}(\mathbb {N})}$
-open. For
![]() $\tau \in V$
, we set
$\tau \in V$
, we set
![]() $u:=\varphi (\tau \ltimes c_{-1})$
as well as
$u:=\varphi (\tau \ltimes c_{-1})$
as well as
![]() $v:=\psi (\tau \ltimes c_{-1})$
and note that
$v:=\psi (\tau \ltimes c_{-1})$
and note that
![]() $\tilde {u}=\tilde {\varphi }(\tau )\neq \tilde {\psi }(\tau )=\tilde {v}$
. This yields
$\tilde {u}=\tilde {\varphi }(\tau )\neq \tilde {\psi }(\tau )=\tilde {v}$
. This yields
![]() $\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
as desired.
$\tau \ltimes c_{-1}\in M_{\varphi ,\psi }$
as desired.
Acknowledgments
The authors thank an anonymous reviewer for their suggestions and corrections.
Funding
This research was funded in whole or in part by the Austrian Science Fund (FWF) [P 32337, I 5948]. This research is also funded by the European Union (ERC, POCOCOP, 101071674). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council Executive Agency. Neither the European Union nor the granting authority can be held responsible for them. The second author is a recipient of a DOC Fellowship of the Austrian Academy of Sciences at the Institute of Discrete Mathematics and Geometry, TU Wien.