Published online by Cambridge University Press: 12 March 2014
The Peanese convention for the use of dots as brackets has the disadvantage that it gives only an awkward method for representing chains of indefinite length, such as the compound implication
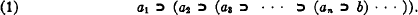
Such chains occur frequently in logical investigations of a metatheoretic nature, and it is convenient to have a systematic method of abbreviating them. The most obvious method of doing this would be to leave the parentheses out entirely, and to understand that in such cases the implication sign or other operation appearing on the extreme left is the most inclusive; but this method, which has been followed by Quine, is at variance with our ordinary algebraic usage, in which we write a − b + c − d for ((a − b) + c) − d, and consequently leads to confusion. It is desirable to have a modification of the Peanese convention which gives a simple method of representing such chain implications, and at the same time avoids this difficulty.
Such a modification is easily obtained by generalizing somewhat a procedure of Church. The latter author uses only a single dot, which he writes on the right of an operator to signify a bracket extending from that point to the end of the formula (or parenthesized expression). If dots are used only on the right of operations this is all that can be desired. But the essential idea of this device can be extended to the case where dots are used also on the left, as follows: let us suppose that a group of dots on the right of an operation or prefix denotes the beginning of a bracket which extends to the right until it meets a group with an equal or larger number of dots on the left of an operation; and that the scope of a group of dots on the left of an operation shall extend to the left until it reaches a larger group of dots on the right of some operation.
1 A system of logistic, Cambridge, Mass., 1934, p. 11 Google Scholar.
2 There is, of course, a notation, due to Łukasiewicz, in which parentheses are dispensed with entirely. This does not come in for consideration here because it requires a change in the order of writing the elementary symbols; in fact, the rules for significance, stated below, are not satisfied.
3 A set of postulates for the foundation of logic, Annals of mathematics, 2 s. vol. 23 (1932), p. 354 Google Scholar.
4 This word is the cognate of German “Zeichen.”
5 This relation is the null relation if no such seniority of operators has previously been defined In the Principia operators are classified into three ranks, viz.: (1) dyadic operators explicitly given; (2) quantifiers; (3) logical product. An operator of higher rank is then taken, in effect, as senior to one of lower rank.
6 I.e. the point which is highest in respect to seniority. Cf. the term “senior officer” in military circles.