Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-22T20:53:24.232Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE UNIFORM COMPUTATIONAL CONTENT OF RAMSEY’S THEOREM

Published online by Cambridge University Press:  09 January 2018

VASCO BRATTKA  and
TAHINA RAKOTONIAINA
VASCO BRATTKA
Affiliation:
FACULTY OF COMPUTER SCIENCE UNIVERSITÄT DER BUNDESWEHR MÜNCHEN NEUBIBERG, GERMANY and DEPARTMENT OF MATHEMATICS & APPLIED MATHEMATICS UNIVERSITY OF CAPE TOWN RONDEBOSCH, SOUTH AFRICAE-mail: [email protected]
TAHINA RAKOTONIAINA
Affiliation:
DEPARTMENT OF MATHEMATICS & APPLIED MATHEMATICS UNIVERSITY OF CAPE TOWN RONDEBOSCH, SOUTH AFRICAE-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the uniform computational content of Ramsey’s theorem in the Weihrauch lattice. Our central results provide information on how Ramsey’s theorem behaves under product, parallelization, and jumps. From these results we can derive a number of important properties of Ramsey’s theorem. For one, the parallelization of Ramsey’s theorem for cardinality n ≥ 1 and an arbitrary finite number of colors k ≥ 2 is equivalent to the n-th jump of weak Kőnig’s lemma. In particular, Ramsey’s theorem for cardinality n ≥ 1 is 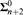${\bf{\Sigma }}_{n + 2}^0$-measurable in the effective Borel hierarchy, but not 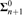${\bf{\Sigma }}_{n + 1}^0$-measurable. Secondly, we obtain interesting lower bounds, for instance the n-th jump of weak Kőnig’s lemma is Weihrauch reducible to (the stable version of) Ramsey’s theorem of cardinality n + 2 for n ≥ 2. We prove that with strictly increasing numbers of colors Ramsey’s theorem forms a strictly increasing chain in the Weihrauch lattice. Our study of jumps also shows that certain uniform variants of Ramsey’s theorem that are indistinguishable from a nonuniform perspective play an important role. For instance, the colored version of Ramsey’s theorem explicitly includes the color of the homogeneous set as output information, and the jump of this problem (but not the uncolored variant) is equivalent to the stable version of Ramsey’s theorem of the next greater cardinality. Finally, we briefly discuss the particular case of Ramsey’s theorem for pairs, and we provide some new separation techniques for problems that involve jumps in this context. In particular, we study uniform results regarding the relation of boundedness and induction problems to Ramsey’s theorem, and we show that there are some significant differences with the nonuniform situation in reverse mathematics.

Keywords

03D3003D7803F6005D10computable analysisWeihrauch latticeRamsey’s theorem
Type
Articles
Information
The Journal of Symbolic Logic , Volume 82 , Issue 4 , December 2017 , pp. 1278 - 1316
Copyright
Copyright © The Association for Symbolic Logic 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Berardi, S. and Steila, S., Ramsey Theorem for pairs as a classical principle in intuitionistic arithmetic, 19th International Conference on Types for Proofs and Programs(Types 2013) (Matthes, R. and Schubert, A., editors), Leibniz International Proceedings in Informatics (LIPIcs), vol. 26, Schloss Dagstuhl–Leibniz-Zentrum für Informatik, Dagstuhl, 2014, pp. 64–83.Google Scholar
Brattka, V., Effective Borel measurability and reducibility of functions. Mathematical Logic Quarterly, vol. 51 (2005), no. 1, pp. 19–44.Google Scholar
Brattka, V., de Brecht, M., and Pauly, A., Closed choice and a uniform low basis theorem. Annals of Pure and Applied Logic, vol. 163 (2012), pp. 986–1008.Google Scholar
Brattka, V. and Gherardi, G., Effective choice and boundedness principles in computable analysis. The Bulletin of Symbolic Logic, vol. 17 (2011), no. 1, pp. 73–117.Google Scholar
Brattka, V. and Gherardi, G., Weihrauch degrees, omniscience principles and weak computability, this Journal, vol. 76 (2011), no. 1, pp. 143–176.Google Scholar
Brattka, V., Gherardi, G., and Hölzl, R., Probabilistic computability and choice. Information and Computation, vol. 242 (2015), pp. 249–286.CrossRefGoogle Scholar
Brattka, V., Gherardi, G., and Marcone, A., The Bolzano-Weierstrass theorem is the jump of weak Kőnig’s lemma. Annals of Pure and Applied Logic, vol. 163 (2012), pp. 623–655.Google Scholar
Brattka, V., Hendtlass, M., and Kreuzer, A. P., On the uniform computational content of computability theory.Theory of Computing Systems (2017), arXiv:1501.00433.Google Scholar
Brattka, V., Hertling, P., and Weihrauch, K., A tutorial on computable analysis, New Computational Paradigms: Changing Conceptions of What is Computable (Barry Cooper, S., Löwe, B., and Sorbi, A., editors), Springer, New York, 2008, pp. 425–491.Google Scholar
Brattka, V., Le Roux, S., Miller, J. S., and Pauly, A., Connected choice and the Brouwer fixed point theorem, preprint, 2016, arXiv 1206.4809.Google Scholar
Brattka, V. and Pauly, A., On the algebraic structure of Weihrauch degrees, preprint, 2016, arXiv 1604.08348.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., On the strength of Ramsey’s theorem for pairs, this Journal, vol. 66 (2001), no. 1, pp. 1–55.Google Scholar
Cholak, P. A., Jockusch, C. G., and Slaman, T. A., Corrigendum to: “On the strength of Ramsey’s theorem for pairs”, this Journal, vol. 74 (2009), no. 4, pp. 1438–1439.Google Scholar
Chong, C. T., Lempp, S., and Yang, Y., On the role of the collection principle for ${\rm{\Sigma }}_2^0$ -formulas in second-order reverse mathematics. Proceedings of the American Mathematical Society, vol. 138 (2010), no. 3, pp. 1093–1100.Google Scholar
Chong, C. T., Slaman, T. A., and Yang, Y., The metamathematics of stable Ramsey’s theorem for pairs. Journal of the American Mathematical Society, vol. 27 (2014), no. 3, pp. 863–892.Google Scholar
Dorais, F. G., Dzhafarov, D. D., Hirst, J. L., Mileti, J. R., and Shafer, P., On uniform relationships between combinatorial problems. Transactions of the American Mathematical Society, vol. 368 (2016), no. 2, pp. 1321–1359.Google Scholar
Dzhafarov, D. D., Cohesive avoidance and strong reductions. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 2, pp. 869–876.Google Scholar
Dzhafarov, D. D., Strong reductions between combinatorial principles, this Journal, vol. 81 (2016), no. 4, pp. 1405–1431.Google Scholar
Erdős, P., Hajnal, A., Máté, A., and Rado, R., Combinatorial Set Theory:Partition Relations for Cardinals, Studies in Logic and the Foundations of Mathematics, vol. 106, North-Holland Publishing Co., Amsterdam, 1984.Google Scholar
Gherardi, G. and Marcone, A., How incomputable is the separable Hahn-Banach theorem? Notre Dame Journal of Formal Logic, vol. 50 (2009), no. 4, pp. 393–425.Google Scholar
Hájek, P. and Pudlák, P., Metamathematics of First-Order Arithmetic, Perspectives in Mathematical Logic, Springer-Verlag, Berlin, 1993.Google Scholar
Hirschfeldt, D. R., Slicing the Truth, on the Computable and Reverse Mathematics of Combinatorial Principles, Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 28, World Scientific, Singapore, 2015.Google Scholar
Hirschfeldt, D. R. and Jockusch, C. G., On notions of computability-theoretic reduction between ${\rm{\Pi }}_2^1$ principles. Journal of Mathematical Logic, vol. 16 (2016), no. 1, pp. 1650002, 59.Google Scholar
Hirschfeldt, D. R., Jockusch, C. G. Jr., Kjos-Hanssen, B., Lempp, S., and Slaman, T. A., The strength of some combinatorial principles related to Ramsey’s theorem for pairs, Computational Prospects of Infinity. Part II. Presented Talks (Chong, C., Feng, Q., Slaman, T. A., Woodin, W. H., and Yang, Y., editors), Lecture Notes Series, Institute for Mathematical Sciences, National University of Singapore, vol. 15, World Scientific Publishing, Hackensack, NJ, 2008, pp. 143–161.Google Scholar
Hirst, J. L., Combinatorics in subsystems of second order arithmetic, Ph.D. thesis, The Pennsylvania State University, State College, PA, 1987.Google Scholar
Jockusch, C. G. Jr., Ramsey’s theorem and recursion theory, this Journal, vol. 37 (1972), pp. 268–280.Google Scholar
Kechris, A. S., Classical Descriptive Set Theory, Graduate Texts in Mathematics, vol. 156, Springer, Berlin, 1995.Google Scholar
Kreuzer, A. and Kohlenbach, U., Ramsey’s theorem for pairs and provably recursive functions. Notre Dame Journal of Formal Logic, vol. 50 (2009), no. 4, pp. 427–444 (2010).Google Scholar
Kreuzer, A. P. and Kohlenbach, U., Term extraction and Ramsey’s theorem for pairs, this Journal, vol. 77 (2012), no. 3, pp. 853–895.Google Scholar
Liu, J., $RT_2^2$ does not imply WKL 0, this Journal, vol. 77 (2012), no. 2, pp. 609–620.Google Scholar
Liu, L., Cone avoiding closed sets. Transactions of the American Mathematical Society, vol. 367 (2015), no. 3, pp. 1609–1630.Google Scholar
Patey, L., The weakness of being cohesive, thin or free in reverse mathematics. Israel Journal of Mathematics, vol. 216 (2016), pp. 905–955.CrossRefGoogle Scholar
Pauly, A., How incomputable is finding Nash equilibria? Journal of Universal Computer Science, vol. 16 (2010), no. 18, pp. 2686–2710.Google Scholar
Rakotoniaina, T., On the computational strength of Ramsey’s theorem, Ph.D. thesis, Department of Mathematics and Applied Mathematics, University of Cape Town, Rondebosch, South Africa, 2015.Google Scholar
Ramsey, F. P., On a Problem of Formal Logic. Proceedings of the London Mathematical Society, vol. S2–30 (1930), no. 1, p. 264.Google Scholar
Seetapun, D. and Slaman, T. A., On the strength of Ramsey’s theorem. Notre Dame Journal of Formal Logic, vol. 36 (1995), no. 4, pp. 570–582, Special Issue: Models of arithmetic.CrossRefGoogle Scholar
Simpson, S. G., Subsystems of Second Order Arithmetic, second ed., Perspectives in Logic, Association for Symbolic Logic, Cambridge University Press, Poughkeepsie, 2009.CrossRefGoogle Scholar
Specker, E., Ramsey’s Theorem does not hold in recursive set theory, Logic Colloquium (Proceedings of the Summer School and Colloquium, Manchester, 1969) (Gandy, R. O. and Yates, C. M. E., editors), North-Holland, Amsterdam, 1971, pp. 439–442.Google Scholar
Weihrauch, K., Computable Analysis, Springer, Berlin, 2000.Google Scholar